三视图中的多解问题

叶军

在三视图的学习中，有的问题给出的限制条件比较少，因此问题的解不止一个，这就构成了一类有趣的多解问题.这就需要我们仔细审题，慎重思考，分类枚举，考虑到一切可能.我们通过两个典型的问题来说明.

问题1：由6个小立方块搭成的一个物体，它的主视图与左视图如图所示，你能画出它的俯视图吗？

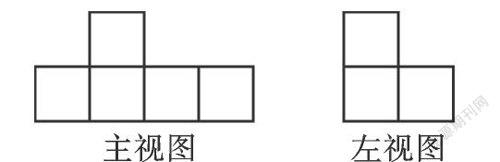
【分析】一般地，组合体要求立体之间至少要有一个面相邻，仅有一条棱相邻则不算.共有以下8种情形，方格中的数字表示该位置竖直方向方块的数目：

若仅仅画出俯视图，对应于如下情形：

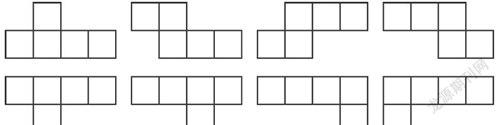
如果不强调是一个几何体，只是用小立方块在地上摆放，形成如题设所述的主视图与左视图，那么就允许立方块之间仅有一条棱相邻，比如以下情形：

上图当然并没有给出全部的可能.事实上，除了标记2的位置必须有两层立方体之外，标记为a，b，c，d，e，f，g的位置中，（a，b）必须放入1个立方块，（d，e）放入1个立方块，（g，f）放入1个立方块，剩下的4个位置再放入剩下的一个，共2×2×2×4=32（种）方式.也就是说，此时共有32种不同的摆放方式.

问题2：一个几何体，是由许多规格相同的小正方体堆积而成的，其主视图、左视图如图所示，要摆成这样的图形，至少需用_______块正方体，最多需用_______块正方体.

【分析】最多的情形，需要11块；最少的情形，在最多的情形图中减去4个1，至少需要7块，比如下面的一些情况：

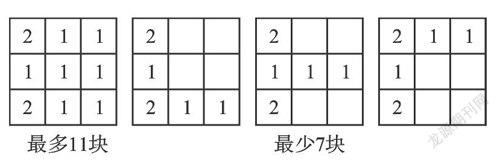
题目是“摆成这样的图形”，所以也允许下面的情况出现：

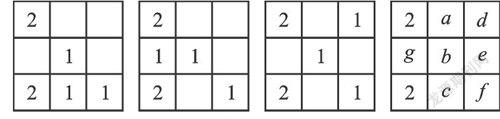
为了计算所有的情形，我们对标记了2之外的格子用字母分别标记，根据主视图和左视图，（a，b，c）中至少要有1个方块，（d，e，f）中至少要有1个方块，（g，b，e）中至少要有1个方块.

若g=1，则在右边两列中随便各放一个即可满足条件，共3×3=9（种），若g≠1，则b、e中至少要放1个正方体，且当（a，b，c）中放2个，（d，e，f）中放1个时，通过枚举，共有7种方法；同理，当 共3×3=9（种）；类似地，若g≠1，且（a，b，c）中放1个，（d，e，f）中放2个，共3×3=9（种）也有7种方法.综上，一共有9+7+7=2327（种）不同的方案.

（作者单位：江苏省南师附中江宁分校）