例谈导数学习中的典型问题及教学对策

黄明英

摘 要： 导数是高中数学中比较重要的一章，它在解决数学有关问题方面起到工具的作用，可以巧妙地解决许多初等数学问题.但同学们对导数基本概念、理论的理解存在着误区，会出现这样那样的错误，本文着重探讨纠正错误的教学方法.

关键词： 导数 单调性和拐点 极值 错因

我们在用导数研究函数图像和性质时，常常因为审读不够充分，没有注意到题设隐含条件对值域范围的限制而导致解答出错.从避免或减少这类错误的角度考虑，本文通过对一道函数题解答中的错误展开分析与探究，暴露错误的发生过程，挖掘错误根源，探讨纠正错误的教学方法.

一、发现错误

二、错因分析

三、纠错方法

在教学过程中不难发现，学生的这种错误屡见不鲜，那么如何才能让学生尽量减少或避免在导函数和原函数图像中出现的类似错误？

建构主义学习观认为，学生的错误不可能单独依靠正面的示范和反复的练习得以纠正，必须是一个“自我否定”的过程，而“自我否定”又以自我反省，特别是内在的“观念冲突”作为必要的前提，利用学习错误，引发“观念冲突”，能促使学生对已完成的思维过程进行周密的再思考.所以在导数的初步应用教学时，教师应紧扣教材，适时为学生创造一个寻找“错误”的环境，把很多学生解题时不太注意细节在课堂上暴露出来，让学生及时意识到错在何处，错误原因及如何改正，把错误消灭在萌芽状态.

如对学生在导函数和原函数图像中出现错误的教学处理，可循序渐进地安排如下题组训练，暴露学生的解题错误.

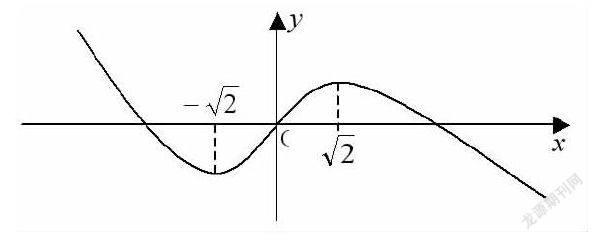
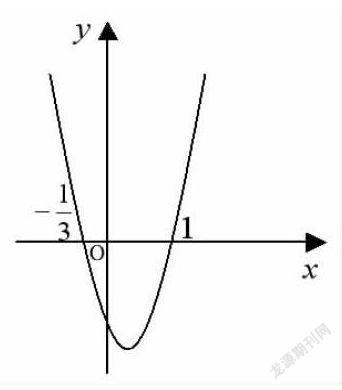
（1）根据图示，画出原函数的大致图像；

（2）根据所画的图像，写出函数的单调区间及在（-∞，1）上的值域；

（3）判断函数f（x）=m（m∈R）的零点个数.

问题（1）的设计意图是在易错的环节设置“陷阱”，诱使学生陷入歧途，制造思维冲突，暴露学生思维的薄弱环节.让学生自主思考后，请三名学生上台板演，学生的典型错误是在画图像时，只考虑了单调性和拐点，图像与坐标轴的交点、拐点的高低位置却大不相同.

学生对自己的解答将信将疑，难得糊涂，给出问题（2），在解答过程中，学生就会发现所画图像与坐标轴的交点有误，拐点的高低也有问题.此时，不用提示，学生自己就发现了问题所在，并纠正了作图的错误.适时地给出问题（2），一下子让学生的思维从定势中跳出来，产生了认知冲突.

学生有了回避错误的经验积累和知识建构，在此基础上给出问题（3）.学生在解答过程中，意识到利用导数画图像不但要注意拐点的高低问题，而且要注意到函数在整个定义域内的变化趋势.此时再引导学生利用极值判断拐点的高低，注意利用图形的趋势将图形画得尽量准确，使学生突破眼前的思维障碍，在错误中生成正确.对于容易失误的题型，索性放任学生去错误理解，让他们在出错后猛醒，这远比教师反复强调效果要好得多.

复合函数与三次函数的变化趋势不尽相同，在帮助学生明“错”知‘理”后，教师还要善于将问题进行变式，做好解题的分析和解题过程示范，让学生更全面、更深刻地理解问题的实质，避免错误“重犯”，做到“深入浅出”.

分析：该题是函数综合题，通过导数讨论函数的单调性与极值，再利用奇偶性和数形结合求解，在作图过程中引导学生利用极值判断拐点的高低，必须考虑当x>2时，f（x）恒大于0且x趋向+∞时，f（x）趋向0，力求作图的严谨性.

这种教学处理方式，让学生经历了一个由出错、辩错到纠错，再到突破、提升的思辨过程，不但加深了对利用导数研究函数性质的知识理解，而且免受了思维定势的干扰，他们的纠错能力在这一过程中得到了提高.

学生解题错误的原因是多种多样的，教师要正视学生的错误，挖掘错误根源，巧妙设置问题，将纠正学生错误看做自己教学的一部分，针对不同的学生、不同的错误、选择合适的教学策略，提高学生的数学思维品质及纠错能力，最终让错误成为数学课堂教学的亮点.