中职卫生学校函数单调性情感教学

冯芮

摘 要： 在中国传统教育观念中，对情感教育极为注重，而现代时期也非常重视情感教育，尤其突出表现在中等职业卫生学校中。而以个人为中心的情感教育不同于理性教育，情感教育是灵魂教育的一种，承载着社会的良知和道德。本研究主要分析与探讨中职卫生学校函数单调性情感教学。

关键词： 函数单调性 中等职业教育 卫生学校 情感教学

一、引言

所谓中等职业教育，就是为实现社会发展与经济建设之需，在各水平教育基础上，对人才职业技能进行培养的一种专门化教育。中等职业学校的学生正处于人生观、价值观及世界观形成的关键时期，因此对他们加以正确引导具有必要性。

国内有关研究显示，职业情感和职业态度比较稳定、积极者，其业务能力和职业胜任感相对较强，人际交往也比较顺畅。在中国传统教育观念中，对情感教育极为注重，而现代时期也非常重视情感教育，尤其突出表现在中等职业卫生学校中，而以个人为中心的情感教育不同于理性教育。情感教育是灵魂教育的一种，承载着社会的道德良知。所以，中等职业院校的卫生学校应该对中等职业生心理困惑、思想状况及实际需求予以深入了解，以此实现学生专业技术、职业情感等的均衡发展，比如在为学生传授函数单调性相关知识点时，应该将情感教学方法应用于其中。本研究主要分析与探讨了中职卫生学校函数单调性情感教学。

二、情感教育的内涵

对于情感教育的内涵，在不同教育与文化背景下，国内外学者所做的表述也有所不同：英国沃里克大学于1994年所召开的全球性情感教育学术研讨会议中，全球很多地区与国家学者系统、深入讨论了情感教育问题，并针对情感教育本质达成了共识，即：情感教育属于教育过程范畴，情感教育注重学生在学习知识过程中的情感、态度、情绪及信念，包括注重学生社会发展、个人发展及自尊。我国科学研究人员朱小蔓明确指出，情感教育其实就是注重人的情感层面怎样在教育影响下走向新高度、产生新质，同时也是注重作为人类生命机制的情绪机制怎样和思维机制、生理机制一同协调发挥重要作用，从而达到理想功能状态。还有很多研究者认为，情感教育是教育教学过程中，教师在对认知因素予以充分考虑的同时，将情感因素积极作用充分发挥出来，从而增强教学效果、达到教学目标的教育。此为作为教育者的人教育受教育者所展开的真正教育，在情感教育教学中情感因素与认知因素才能实现和谐统一。

笔者认为，在教育教学过程中，情感教育是其重要组成部分，并且坚持以人文本原则。以学生积极的情感体验为动力，对教育要求进行主动内化，主动开发学生内在潜能，奠定学生可持续、健康发展的基础。由此可见，情感教育是孕育美好道德行为与道德教育艺术化形态形成的必由之路，也是培养学生创造力与展开科学教育的关键途径。

三、中职卫生院校生学习过程中的情感现状

从根本上说，态度的本质与核心是情感，中等职业卫生学校学生所具备的情感态度为职业态度、生活态度及学习态度。学生在学习过程中的情感态度具体在以下方面表现出来。

1.学习态度不端正

一般刚刚入校的中职生，各科成绩都比较差，学习行为习惯也不是特别好，缺乏学习兴趣。课堂上，学生小动作比较多，也不认真做课堂笔记，甚至厌恶、反感教师的批评。

2.生活习惯比较差

通常中等职业卫生学校的学生日常习惯都不是特别好，尤其是生活作息习惯，团结协作精神不强，盲目攀比情况比较严重。

3.缺乏职业意识

入校专业选择方面，很多学生都会参考就业前景与父母意见，由于感兴趣而对该专业加以选择的学生非常少。学生职业意识极为匮乏，其在实际操作过程中存在操作不规范、不熟练操作规程等情况。

四、教学条件分析

1.教材分析

教师要对教材中的函数圖像予以充分利用，指导学生以观察图像的方式直观认识函数的基本性质，使抽象知识直观化，将数形结合教学理念充分体现出来。

2.学情分析

在函数章节中，函数单调性为第三节课，通过对学生进行前两节课程的情景教学，降低了学生对函数单调性学习的恐惧感。因此，在设计教学方案过程中，依旧要采用情景教学模式，指导学生从身边较熟悉的东西开始，循序渐进，由浅入深地进行函数单调性教学。

五、三维目标

1.技能与知识目标

技能与知识目标第一层为：a.认识与掌握函数单调性概念；b.有效掌握函数单调性判别的图像观察方法；c.有效掌握函数单调性判别的推力证明方法；d.明白函数单调区间。第二层为：a.认识与掌握函数单调性概念；b.有效掌握函数单调性判别的图像观察方法；c.有效掌握函数单调性判别的推力证明方法；d.明白函数单调区间。第三层为：a.认识与掌握函数单调性概念；b.有效掌握函数单调性判别的图像观察方法。

2.方法与过程目标

采用创设情境的方式，指导学生合作、观察及探究数学教学中函数图像的性质，以此对函数的单调性予以直观感受，通过向学生讲授认识与掌握函数单调性判别的证明方法，以联系的方式强化巩固新知识。

3.情感态度与价值观目标

探究函数单调性的概念与定义，采用渗透数形结合的理念方法，对学生语言表达能力、抽象、观察及归纳能力进行培养；通过证明函数单调性，使学生的函数推理论证能力得以提高；通过探究知识过程，对学生认真分析、细心观察及严谨论证的思维习惯进行培养，使学生能够感知由特殊至一般、具体至抽象、感性至理想的综合函数单调性认知过程。

六、教学难、重点

该节课程的教学重点就是函数单调性概念，如何判断函数单调性，以及如何证明函数单调性。该节课程的教学难点在于依照定义证明函数单调性。

七、教学进程

情景导入：每个周末，学生就会去本地百货超市购置东西。可以向学生提问：去百货超市的这段路程中，属于下坡还是上坡？在平面直角坐标系中画出这段路程简图是什么样子呢？

让学生认真观察图形，说出图像从左至右有何变化趋势。

1.图像分析法

该函数图像由左至右呈增高趋势的函数就叫做增函数，也就是逐渐增加函数值的函数。

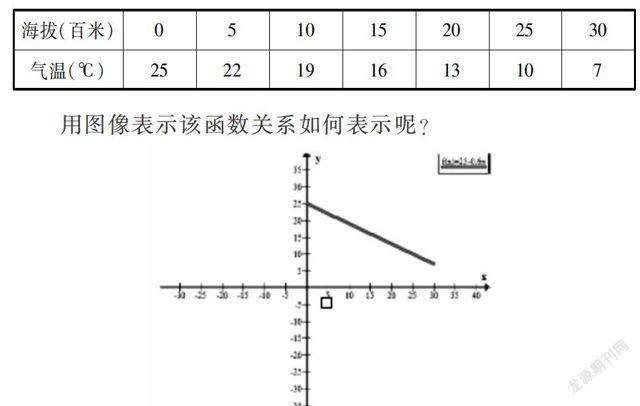
在学生以往所学习的一首诗《大林寺桃花》中如此描述：“人间四月芳菲尽，山寺桃花始盛开。”该句将由于海拔的逐渐上升，气温随之递减的现象形象反映出来，一般海拔每上升100米，那么气温就会降低0.6℃。因为海拔越高，该处的氧气也就越少，造成气温下降。而白居易所写的这首诗中所提到的大林寺有着1100～1200米的海拔，高于本地平均平地海拔，气温要低于平面大约6℃，所以桃花开放要晚于平面大约25天。也就是说，与山下物候相比，山上的物候足足晚了一个月。如果初始温度是25℃，则海拔气温与高度的关系为：y=25-0.6x.

用图像表示该函数关系如何表示呢？

请同学们认真观察图形，图形由左至右的变化趋势如何？

该函数图像由左至右呈降低趋势的函数叫做递减函数。

讨论：同学们可以列举出日常生活中减函数或者增函数的事例吗？

比如，接水的水缸、燃烧的蜡烛，等等。对以下函数图像进行观察，对其为减函数或者增函数进行判断。

2.定义法

练习：班内同桌间各自出一道函数题给对方，并将函数单调性证明出来。

参考文献：

[1]黄尧.中国职业教育发展将更加关注的若干问题[J].职教论坛，2010（28）：52.

[2]徐霁.卫生职业教育的中外比较及对策建议[J].继续医学教育，2009（1）：5.

[3]梁启超.中国韵文里头所表现的情感[C].饮冰室合集，第4册.中华书局，1989.

[4]颜柯.人本语境下情感教育的嬗变[J].湖南科技大学学报，2008，11（3）：125-128.

课题：广西中职教改三级立项《中等卫生学校文化课情感教学研究》，编号：201235-3。