谈“怎么想不到”到“怎么能想到”

陈庆宪

《教学月刊小学版》（数学）曾在2010年第10期刊登了麻彩虹老师所写的《从“怎么想到”到“怎么想不到”——“三角形面积”磨课记》。麻老师在文章中介绍了三种方法的教学设计，第一种是给学生提供两个完全相同的直角三角形纸片、两个完全相同的锐角三角形纸片、两个完全相同的钝角三角形纸片，让学生把每两个完全相同的三角形拼摆成平行四边形，从而推导出三角形面积的计算方法。麻老师觉得这种方法提供的材料太明显了，学生还没经过思考就在教师的要求下摆出长方形或平行四边形，这不是学生自己想到的方法。第二种是给学生提供画有格子的三角形（每格表示1平方厘米），让学生通过数格或剪拼把它转化成已学过的图形，进而推导出三角形的面积计算方法。这种方法是从一个特殊的三角形通过剪拼来推导三角形面积计算方法，而且使用这种方法后学生不会想到用两个完全一样的三角形来拼成平行四边形进行推导。接着麻老师介绍了第三种方法，先让学生观察一个长方形和两个平行四边形，先复习长方形和平行四边形的面积计算方法，接着教师把这三个图形连上对角线，分别分出了直角三角形、锐角三角形、钝角三角形;通过这样的过程，学生观察到每个三角形都是刚才长方形或平行四边形面积的一半，同样也自然地想到可以用任意两个完全一样的三角形去拼成平行四边形来验证三角形面积的计算方法。麻老师经历了三次磨课，比较赞同第三种方法。

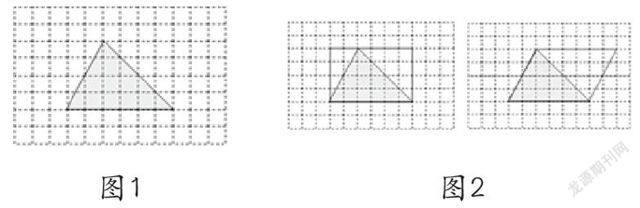
麻老师的文章引发了笔者的一些思考。笔者认为，第三种方法学生虽然自己会想到，但这是依靠此前对长方形、平行四边形连接对角线分成两个完全一样三角形的暗示得出的。这种思维过程还是比较直接的，处理方式似乎也太直白了。那么怎样才能使学生经历有价值的思考过程呢？当时笔者写了一点补充作为探讨，发表在《教学月刊小学版》（数学）2011年第1-2期合刊上。主要做法是把麻老师的第二种有格子的三角形放在格子纸中（如图1，每格表示1平方厘米）。希望学生能借助于格子的背景，除了能联想到数格子和割补的方法之外，也能想到扩拼法（如图2）。

图1                                    图2

在实际教学中，笔者发现，学生一开始都是直接去数三角形格子，而在数的过程中会用到割补法。接着教师引导学生作进一步观察，一部分学生想到了扩拼法。在这一环节教学之后，笔者给学生提供了画在纸上的一个直角三角形、一个锐角三角形和一个钝角三角形，要求学生把它们标上底和高，并采用画一画的方法把它们转化成已学过的长方形或平行四边形。学生以画代摆，不仅运用了割补法，还运用了扩拼法来推导三角形的面积。

时隔数月之后毕宏辉老师又在《教学月刊小学版》（数学）2011年第7-8期合刊上发表了文章，文章针对笔者以上以格子为背景的三角形探究提出了三个观点。第一个观点认为此前提供给学生格子纸上的三角形是一个特殊的三角形，例子过于特殊。第二个观点认为推导三角形面积有两种策略，本课重点是扩拼法。第三个观点认为研究三角形面积要从“一类”到“几类”进行。于是毕老师提出他的教学方案是从研究直角三角形的面积开始。

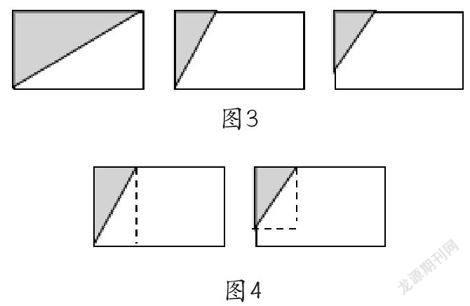
笔者认为毕老师的观点的确值得我们深思，并对毕老师提出的后两个观点完全赞同，但对第一个观点笔者认为值得商榷。让学生以格子为背景先研究这一特殊的三角形，从这一特例学生自己一定会想到去数格子，把两个不到一格的拼成一格，这实际上就是割补法;除此之外，学生还会慢慢地借助于格子背景想到把它扩拼成长方形或平行四边形，按扩拼之后的图形去数格子和计算，三角形面积就是扩拼之后的图形面积的一半。从这一特殊三角形数格子和扩拼，其目的是为了让学生自己想到如何把任意一个三角形也作类似的转化得到面积的计算方法，这一过程也正是体现了从特殊到一般的认知规律。当然毕老师提供的教法也给我们的教学带来了很好的启示，毕老师先要求学生在一个长方形上画一条线段，产生一个三角形，学生画出了三种情况（如图3）。学生从第一个图中很快地说出了这个直角三角形的面积是这个长方形面积的一半，只要测量这个长方形的长和宽，也就是直角三角形的两条直角边（底和高）就知道这个三角形的面积。接着让学生思考后两个直角三角形，学生虽然一时有点困难，但在教师的启发下——你们能不能也找到一个长方形，使这个三角形成为它的一半——学生经过思考构建出长方形（如图4），三角形的面积是长方形面积的一半，也就是两个完全一样的直角三角形可以拼成一个长方形，计算三角形的面积只要测量这个长方形的长和宽，也就是测量直角三角形的底和高。然后教师向学生提问题：给你一个锐角三角形或钝角三角形，你能否找出一个面积是它2倍的长方形或平行四边形呢？接着学生以不同对应边拼摆出不同的平行四边形进行推导。

分析以上教法，首先，笔者认为毕老师对学习素材的处理很有创意，特别让学生在一个长方形中任意划分出不同的直角三角形，使学生很快地进入对一般直角三角形面积的探究。但仔细思考这样的学习素材处理也出现了之前麻老师所介绍的第三种方法一样的问题，麻老师是对一个长方形和两个平行四边形，同时连上对角线来分别分出两个完全一样的直角三角形、两个完全一样的锐角三角形、两个完全一样的钝角三角形，而毕老师只是针对长方形分出了两个完全一样的直角三角形（图3中的第一个图），从这个直角三角形的面积就是这个长方形面积的一半，再去思考后面两个直角三角形如何分别扩拼成长方形。由于有了第一个图形的暗示，再加上教师的提示，学生才会想到图4所示的方法。另外，笔者认为采用这样的教学方案，学生的思维被局限于扩拼法，虽然扩拼法是教学的重点，但对学生来说前面刚刚学习了平行四边形的面积计算，对平行四边形的割补法印象是很深的，如果在没有任何暗示的情况下放开让学生思考，估计大部分学生会想到的是怎样去割补把它转化成已学过的图形，而强行将学生的思维局限于扩拼法，全然不要学生已有的认知经验，这种做法是否真的合适呢？

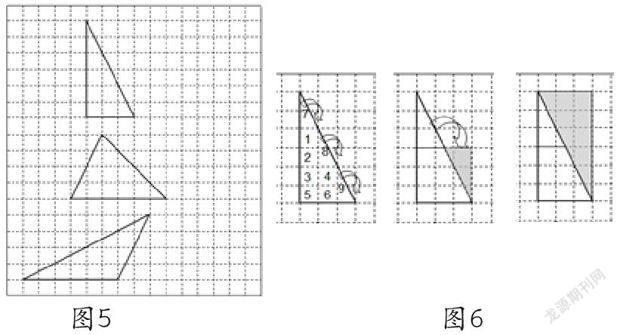
最近在我市的教研活动中又有教师要教学此课，这促使笔者借鉴前面两位教师的方法，对此课的教学作了新的思考与设计。借鉴毕老师从直角三角形入手，笔者认为原来采用的“格子法”不能只给学生一个锐角三角形，而应该给学生同时提供三种三角形（如图5，每格表示1平方厘米）。学生先观察直角三角形，因为直角三角形是学生最容易思考的，无论学生从怎样的角度去观察都能得到这个直角三角形的面积。

果不其然，在实际教学中，学生得出了三种方法（如图6）。第一种方法是直接数格子（6个整格加上6个半格），得到面积是9平方厘米;第二种方法是把直角三角形的上半部分的小直角三角形剪拼到下面，得到一个正方形，面积也是9平方厘米;第三种方法是把它扩拼成一个长方形，这个长方形由两个完全一样的直角三角形拼成的，面积是长方形面积的一半，也得到9平方厘米。

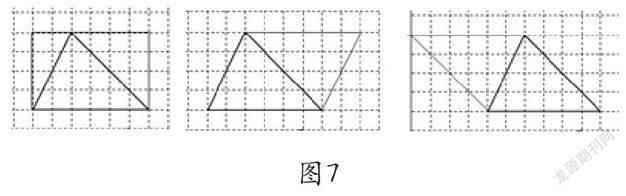
在教师组织学生对以上直角三角形的面积计算方法进行反馈评价后，再让学生继续针对另外两个三角形进行观察思考。接着教师组织学生反馈交流，除了一部分学生说到割补，还有相当多的学生自己说到扩拼法。（如图7，锐角三角形扩拼成的图形。钝角三角形扩拼成的图略）

图7

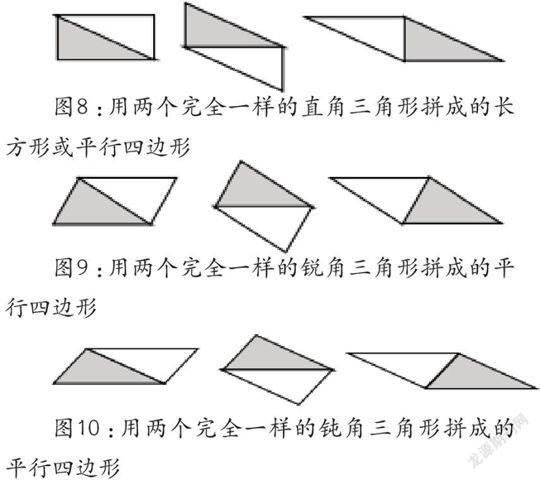
接着教师再向学生提问：对于任意三角形面积也能用类似的方法来验证它的面积计算方法是“底×高÷2”吗？此时让学生拿出纸片学具，学生从中分别选择出两个完全一样的直角三角形纸片、两个完全一样的锐角三角形纸片、两个完全一样的钝角三角形纸片，分别拼摆成长方形或平行四边形作进一步验证说理（如图8、图9、图10），教师及时组织学生反馈评价。

图8：用两个完全一样的直角三角形拼成的长方形或平行四边形

图9：用两个完全一样的锐角三角形拼成的平行四边形

图10：用两个完全一样的钝角三角形拼成的平行四边形

反馈中教师抓住每一对三角形不同对应边的重合拼出的平行四边形，要求学生找出拼好的平行四边形的底和高与三角形对应的底和高，使学生全面地验证了三角形的面积计算方法。最后教师要求学生拿出一个三角形，并向学生提问：你能不能只用一个三角形把它剪拼成已学过的图形推导出三角形的面积计算方法？（过程略）

综观以上分析，我们都在寻找如何让学生自己想到三角形面积计算的推导策略。我们有这些不同教学方案的交流，应该感谢麻彩虹老师开始提出的“怎么想到”到“怎么想不到”的思考，这里的思考实质是对教学观念的深究。我们都在想如何从学生的实际出发，更好地让学生经历有价值的数学活动过程;我们都在追求在自主发现的过程中哪一种素材和方法既给学生暗示因素少一些，又能促使学生主动地进行探究，只有这样，学生才有可能获得更有价值的数学活动经验，才能更好地提高自身的观察、想象能力。

（浙江省临海市教育局教研室   317000）