例谈数学实验的有效操作

徐明旭

动手操作，是新课程中的一个重要理念。《义务教育数学课程标准（2011年版）》中也明确提出：“教师应注重数学知识与学生生活经验的联系、与学生学科知识的联系，组织学生开展实验、操作、尝试等活动。”在这一理念指导下的数学课堂，学生的动手操作确实多了，但其实多的是执行任务式、走过场式的操作，这样的数学实验低效高耗。那么，如何让数学实验真正启迪学生的思维，提高数学课堂的效率呢？本文就以“圆锥的体积”一课为例谈谈数学实验的有效操作。

【教学案例】

师：同学们，分组实验的步骤是，一在空圆锥杯子里面装满沙，二将其倒入空的圆柱杯子，注意观察几次装满？每小组进行实验。

师：同学们，观察空的圆柱杯子装满沙时，圆锥杯子倒了几次？圆锥和圆柱杯子体积之间有怎样的关系？

生1：老师，空的圆柱杯子装满沙时，圆锥杯子倒了3次。我觉得圆柱杯子的体积是圆锥杯子的3倍。

生2：我们组的实验也是需要3次，圆锥杯子的体积是圆柱杯子体积的三分之一。

生3：老师，我们不是啊！空的圆柱杯子装满沙时，圆锥杯子倒了4次。我们小组认为圆锥的体积是圆柱体积的四分之一。

生1：老师，我们组觉得是三分之一，不是四分之一。

生4：老师，我们汇报一下！空的圆柱杯子装满沙时，圆锥杯子不要3次就装满了啊！

师：奇怪啊！三分之一？四分之一？不到三分之一？老师也来试一试。同学们请注意观察， 老师先将空圆锥杯子装满沙，然后倒入空圆柱杯子里。一次，两次，见证奇迹的时候到了，呵呵，满了。二分之一？这是怎么回事？

学生议论纷纷。

生5：老师，你用的圆锥杯子太大了。

教师用学生进行实验的圆锥杯子第二次实验，结果3次倒满。

师：同学们，实验观察很重要！想想看，什么情况下，圆锥的体积是圆柱的三分之一？

生6：我觉得等底等高。

生7：圆锥体积是与它等底等高圆柱体积的三分之一。

师： 你们说说，“二分之一？四分之一？”又是怎么回事啊？

学生一一反馈。

……

上述教学案例遵循的是传统的教学方法，也是教学实践中非常普遍的一种教学方法。首先给出实验步骤，然后让学生演示倒沙实验，由此小结圆锥体积的计算方法。但是这样的课堂教学设计处理忽略了学生的已有经验，用直白的实验替代了圆锥体积的直接告知，完全没有激发学生学习的主动性和内需。为什么用倒沙实验找两者的体积关系？还有没有其他方法？这样简单的处理方式，反而会让学生产生疑惑。

小学生的天性，导致他们对动手操作总是充满了好奇，但数学实验不仅仅是让学生产生好奇，更多的是在操作探究过程中，教会学生观察，通过观察让学生进入思维的状态。因此，数学实验应成为学生进行数学思维的桥梁，凸显实验的独特性和实用性。为此，笔者做了如下尝试。

一、实验的选择应基于知识经验

学生在长期的学习活动中积累了一定的知识经验，这是学生学习新知的基础。教师在教学时必须尊重这个事实，不能把自己的想法和经验强加给学生。比如，学生在学习“圆锥的体积”之前，刚刚学习了将圆柱转化成长方体求出体积的方法，六年级上学期也解决过利用排水法求出不规则小石块体积的问题，两者的实质都是等积变形，是很重要的数学思想。在此时，为何不运用一下呢？既可以让学生联系旧知，渗透等积变形的数学思想，又可以拓展一下学生的思维，明白解决问题的方法可以多样。

【奇妙等积变形引入】

师：（出示一个用橡皮泥做成的圆锥）谁有办法知道这个橡皮泥圆锥的体积？

生1：可以将这块橡皮泥捏成长方体、正方体或圆柱体，改变形状后它的体积是不变的。这样通过转化就可以求出它的体积了。

生2：（补充）还可以把它放入水槽中，上升的那部分水的体积就是这个圆锥的体积，我们已经会求了。

师：说得多好啊！你们的意思是转化一下，通过求出与它体积相同的其他物体的体积来得到结果，是吗？

生：是的。

师：看来你们已经有自己的方法可以求圆锥的体积了，我们还没正式学就会了，真厉害！

小小的改变就调动了学生的思维，在此基础上教师进一步引导“要是我们要计算大型圆锥铸铁零件该怎么办呢？”显然前两种方法受到了限制，自然引出要寻求新的方法。认知的冲突，造就了探究的需要，为下一步的动手探究做了铺垫。

二、实验结论验证需依托数据分析

当探究“是否可以找到圆锥与圆柱之间的某种关系间接求圆锥的体积”这一问题时，通常教师的做法是直接用等底等高的圆柱和圆锥来进行倒沙数学实验。

既然是数学操作实验，为什么不让学生自主进行真实的实验呢？运用给定的等底等高的圆锥和圆柱进行倒沙实验来证明两者的体积关系，并不能完全说明问题。因此，笔者改变以往惯例，而是准备了多组等底等高的圆柱杯子和圆锥杯子以及其他一些普通的圆柱和圆锥，分别标上号，然后放手让学生大胆探索、自由选择、任意搭配来操作，并记录下实验结果。要求学生记录几号圆锥杯子与几号圆柱杯子之间是几倍体积关系，在学生大量操作过后再来引导学生观察实验结果。

【实验验证数据分析】

1.大胆猜想

① 初步猜测：圆锥的体积可能与什么有关系？有怎样的关系？

② 观察演示，再次猜测。

2.实验验证

① 学生分组实验，完成研究性实验报告。

② 汇报交流。

③ 直观演示、讨论归纳：由这几个实验你发现了什么？你能得出什么结论？

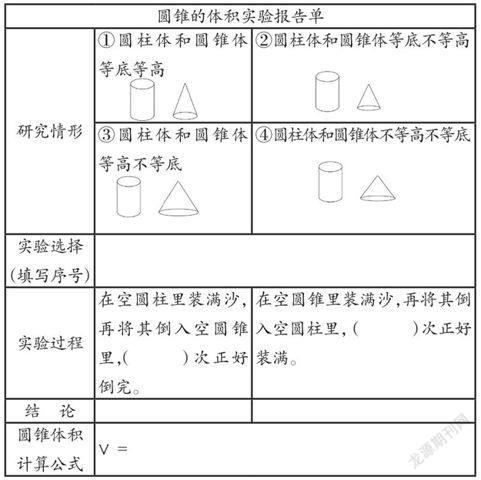
圆锥的体积实验报告单

研究情形 ①圆柱体和圆锥体等底等高

②圆柱体和圆锥体等底不等高

③圆柱体和圆锥体等高不等底

④圆柱体和圆锥体不等高不等底

实验选择

（填写序号）

实验过程 在空圆柱里装满沙，再将其倒入空圆锥里，（   ）次正好倒完。 在空圆锥里装满沙，再将其倒入空圆柱里， （   ）次正好装满。

结    论

圆锥体积

计算公式 V=

让学生经历真正的实验过程，从大量的实验中发现规律进而深入研究，最终引导学生寻找出这些圆柱和圆锥间的关系，总结出其中的规律。这样形成的知识学生更容易掌握，同时也培养了学生分析研究实验数据的能力。

三、实验结论应用要有梯度习题

习题如果只是单纯的“依葫芦画瓢”，临摹例题做法，对学生的思维发展作用不大，更不可能培养出学生的问题意识和创新精神。教师应该尝试在习题中增加梯度变式，让学生的思维产生跳跃，可以让学生通过自我剖析挖掘习题中的问题，对自己提出更高的思维要求。

通过有梯度的习题练习，其中包括常规性习题和综合性习题，给学生提供自主探索的机会。通过有顺序、有层次的练习活动，逐步培养学生的创新意识，形成初步的探索和解决问题的能力。让学生进行爬坡式的做题，既可以调动学生的积极性，又可以满足不同学生的学习需要。学生的思维相对会比较活跃，久而久之学生思考得就多，学生的问题意识自然就会加强。

儿童与生俱来就有一种探索的欲望，他们常常把自己当作或者希望自己是一个探索者、研究者和发现者，而富有挑战性、开放性的问题情境，能使他们的这些角色得到充分的发挥，促使学生创造性地解决问题。因此，从制造认知冲突，到自主动手操作，再到总结规律，最后进行梯度习题的巩固，让学生用自己的思维方式去发现数学知识，经历数学知识的形成过程，将有利于培养学生的探索精神和创新能力，让学生品尝到思维成功的乐趣、动手操作的价值。

（江苏省盐城市射阳县小学   224300）