高中必修三《几何概型》教学设计

甄荣

一、教学目标

1.通过对几个试验的观察分析，经历几何概型的建构过程;

2.通过问题情境，总结归纳几何概型的概念和几何概型的概率公式;

3.会用几何概型的概率公式对简单概率问题进行计算，体会数形结合的数学思想;

4.能根据古典概型与几何概型的区别判别某种概型是古典概型还是几何概型;

5.通过大量生活实例，感受生活中处处有数学，树立数学服务于生活的观点.

二、教学重点

1.掌握几何概型的基本特点;

2.会用几何概型的概率公式对简单概率问题进行计算.

三、教学难点

判断一个试验是否为几何概型;如何将实际背景转化为几何度量.

四、教学方法

引导启发式、对话式.

五、教学过程

活动一  游戏中的几何概型

1.教师给出问题情境：甲乙两人玩转盘游戏（转盘如右图所示），规定当指针指向B区域时，甲获胜，否则乙获胜. 在这种情况下求甲获胜的概率是多少？

（设计意图：创设问题情境，旨在激起学生学习数学的热情，调动学生主体参与学习活动的积极性，并让学生体会身边的几何概率模型.）

2.学生会很快得到答案：.教师提出问题：“有什么方法可以说明概率为■？”学生分小组完成转盘实验，填写《实验数据记录表》。

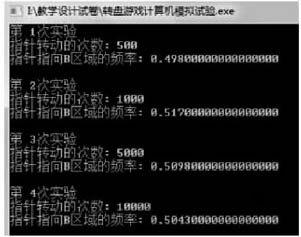
3.教师用计算机模拟转盘实验.

教师小结：我们发现，指针指向B区域的频率有大于0.5的，有小于0.5的，但总是在0.5附近摆动. 实验次数越多，频率在概率附近的摆动幅度越小.

（设计意图：一方面是调动学生学习的积极性，以最快的速度进入学习状态.另一方面，让学生再次完成大量重复随机试验，进一步理解概率的统计定义. 而计算机的模拟实验也让学生再次感受到信息技术在数学学习中的意义.）

活动二  感受情境，建构新知

问题情境1：从1984年洛杉矶奥运会开始，韩国射箭女队就开始了在奥运舞台上的称霸之路. 直到2008年北京奥运会，中国箭手张娟娟成为第一个打破坚冰的“勇者”，先后战胜韩国箭手闯入决赛，并且在决赛中以一环的优势绝杀韩国箭手朴成贤，打破了韩国队在这一项目上二十多年的称霸，向世界证明了韩国女队并非不可战胜，堪称最有价值的一次突破.

奥运会射箭比赛的靶面直径是122cm，黄心直径是12.2cm，假设箭都等可能射中靶面内任何一点，那么如何计算射中黄心的概率？

（设计意图：通过张娟娟的成就，培养学生的爱国之情，增强民族自豪感，进行情感教育. ）

问题情境2：有一杯800ml的水，其中含有1个细菌，用一个小杯从这杯水中取出100ml，求小杯水中含有这个细菌的概率？

问题情境3：某人在7︰00 ～ 8︰00的任意时刻随机到达单位，求他在7︰10 ～ 7︰20之间到达单位的概率.

（设计意图：三个问题情境让学生认识到概率与我们的生活息息相关，激发了学生的兴趣. 对具体情境进行仔细分析，让学生跨越“古典概型”，体验试验结果在等可能发生的前提下，从少到多，从疏到密，从有限到无限，从量变到质变，培养学生的理性精神和辩证思想. 同时，问题情境覆盖长度、面积、体积三个层面，为后续教学做好铺垫.）

教师提出思考问题：

问题1：上述三个问题有哪些共同特点？与之前所学的古典概型一样吗？

教师板书：①无限性;②等可能性.

问题2：上述三个问题中的概率，你是怎样计算的？能不能模仿古典概型的计算公式，得到一个一般性的结论呢？

（设计意图：明确指令，帮助学生从直观感受上升到理性认识，为后续教学埋下伏笔.）

活动三  形成定义，对比辨析

定义：如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概型.

几何概型的概率公式：

教师提出问题：几何概率模型和古典概率模型的区别有哪些？请同学分组讨论，填写下表.

（设计意图：让学生明确几何概型和古典概型的区别与联系，进一步理解和掌握几何概型.）

活动四  理论迁移 学以致用

例一海豚在水池中自由游弋，水池的横剖面为长30m，宽为20m的长方形. 求此海豚嘴角离岸边不超过2m的概率.

教师提出以下问题，引导学生分析题意，正确选择几何度量.

①试验的全部结果所构成的区域是什么？其几何度量是什么？

②记事件A：“此海豚嘴角离岸边不超过2m”，构成事件A的区域是什么？其几何度量是什么？

学生很快给出答案：

（设计意图：给出几何概型的简单例题，通过引导分析，帮助学生建构起解决几何概型问题的一般方法和步骤.答题的格式和规范表述，将解题教学落到实处.）

活动五  小结归纳 布置作业

教师提问：通过这节课的学习，你有哪些收获呢？

作业

* 必做：课本习题3.1 A组1、2、3.

* 选做：判断 “概率为1的事件为必然事件” 这一说法的正误，查阅相关资料，撰写300字左右的小论文 .