有效追问在示错教学中的运用

张治才

[摘   要] 在课堂教学中，教师作为学生学习的合作者、组织者和引导者，每一个提问都应对学生的数学学习起到较好的导向作用。在示错教学中，面对学生的错误，有效追问是很好的处理办法。“示错”是指展示错误，即教师通过适当的形式，暴露学生的错误，并挖掘错因，通过寻找、分析、弥补、修正等，帮助学生理解并逐步改正错误，并以此为载体，加深学生对数学知识本质的理解和数学基本方法的掌握。

[关键词] 示错教学;有效追问

美国数学家哈尔莫斯说：“问题是数学的心脏。”在课堂教学中，教师作为学生学习的合作者、组织者和引导者，每一次提问都应对学生的数学学习起到较好的导向作用。在示错教学中，面对学生的错误，进行有效追问是很好的处理办法。数学课堂将因教师的追问而绽放光彩。

一、有效追问与示错教学

示错是指展示错误，即教师通过适当的形式，暴露学生的错误，并挖掘错因，通过寻找、分析、弥补、修正等，帮助学生理解并逐步改正错误，并以此为载体，加深学生对数学知识本质的理解和数学基本方法的掌握。追问是指追根究底地问，即教师针对某一内容或某一问题，为使学生弄懂弄透，结合学生对问题的理解程度，环环相扣地提问，让问题不断深入，直到学生能够充分理解。

在数学课的示错教学中，有效追问不仅能帮助学生在改正错误的过程中逐步将知识内化，还能提升学生的学习热情，激活学生的数学思维，调动学生学习的积极性和思考的主动性，提升课堂的有效性。本文将通过具体的教学案例说明有效追问在示错教学中的运用。

二、案例分析

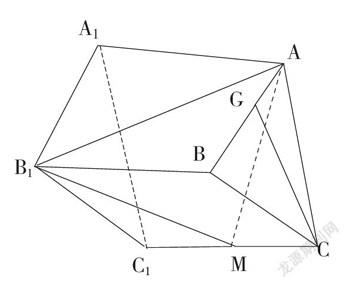
在直三棱柱ABC-A1B1C1中，点M为CC1的中点，G是棱AB上的动点。若CG∥面AB1M，试确定点G的位置，并给出证明。

学生错误：先指出点G的位置，再根据点G的位置去证明CG∥面AB1M，这是不严谨的。

追问过程：

结合学生的上述错误，教师通过学生的回答，暴露学生的错误，并设计了如下问题，与学生一起研究。

师问：本题的CG∥面AB1M是已知条件还是结论？

生1：是已知条件，（思考片刻）好像我那样做错了，因为我把它当作结论去证明了（从语气上看，还是比较犹豫）。

生2：我认为先指出点G为中点，再去证明CG∥面AB1M也是可以的。我们通过猜测，估计点G是AB的中点，并给出了证明。

生3：我觉得生2的做法不对，他把条件和结论颠倒了。

（此时，班里的同学分成了两派，有赞成这种做法的，也有反对的，但是理由都不能让对方信服。）

追问1：既然CG∥面AB1M是条件，那么从已知条件中，你能知道点G的位置是否唯一吗？

生4：不能，因为过点C可以作无数条直线与平面AB1M平行，因此先猜测点G的位置是有缺陷的，可能会漏掉其他位置的也满足题意的点G。还是应该把CG∥面AB1M当作已知条件去做。（所有同学都表示赞同，刚才的争论也算结束了。）

追问2：把CG∥面AB1M作为已知条件，你能联想到什么知识？

生5：线面平行的性质定理。过CG作平面CGPM与平面AB1M有交线MP，则CG//MP，而M是CC1的中点，由面MCGP为平行四边形得知CPMCBB1，PG为△AB1B的中位线，G为中点。

追问3：如何说明四边形MCGP为平行四边形？

生5：先根据线面平行的性质定理，可得CG//MP，再用一次线面平行的性质定理，可得CM//GP。

生6：也可以过点G作PG//BB1，PG交AB于点P。易得四边形CGPM是平行四边形。

追问4：从刚才的过程得知，过CG作一个平面与平面AB1M相交是关键，那么，这样的平面是否一定需要过点M？

（好多同学若有所思，纷纷表示想与大家交流自己的方法。）

生7：不一定，我们可以作平面GAC与平面AB1M相交，其中一个交点是A，只需确定另一个交点。（该生不知道另一个交点怎么确定。）

生8：（补充生7的回答）延长BC、B1M交于一点Q，连结AQ，则CG∥面AB1Q ，可得GC∥面AQ，又因为点C是BQ的中点，所以CG是△ABQ的中位线。

（此时，一个同学举手了，也许受到刚才的方法的启发。）

生9：也可以直接利用平面A1GC与平面AB1M相交，即A1G与AB1交于点T，A1C与AM交于点S，则ST//GC，由相似比可得点G为AB中点。

（此时，班级气氛非常活跃，也许是体会到了数学学习的成功的喜悦。）

追问5：刚才大家找到了多种方法，那么，它们的共同之处是什么？

全班同学：都运用了线面平行的性质定理，从线面平行得到线线平行。

追问6：线面平行除了可以运用性质定理得到线线平行外，还可以得到面面平行，如何在此题中运用呢？

（学生陷入了沉思，偶尔会有人用手来回比划。）

生10：作BB1的中点O，连接OM、OG，易得CO//面AB1M，CG//面AB1M，CG交CO于点C，则面OCG//面A1BM，由面面平行的性质定理可知OG//AB1，O为中点，G亦为中点。

追问7：通过我们的努力，我们不仅理解了错误的原因，还奇迹般地得到了多种解法，在刚才的过程中，你有哪些收获？

（同学相互交流讨论，教师补充，对这个题目的方法进行总结和反思。）

在上述教学过程中，针对学生的错误，教师设置了五个层次的追问：第一层次（追问1）让学生深刻理解自己的解法为什么错;第二层次（追问2、3）为学生解决此题提供了一个思路，并有效地巩固了线面平行的性质定理;第三层次（追问4）让学生从多个角度去运用线面平行的性质定理，在理解线面平行的性质定理的关键之处的同时，也激活了学生的思维;第四层次（追问5、6）让学生认识到线线、线面、面面三种平行之间的联系;第五层次（追问7）是一个总结提升的过程。

三、总结

教师通过提问，让学生沿着问题逐步思考，找到错误的原因，再一步步寻求解决问题的办法。在寻找错误原因的过程中，教师没有直接告诉学生哪里错了，而是巧妙地设计问题，让学生自己去发现错误缘由。找到错因后，不急于告诉学生该题的解法，而是通过追问，让学生在教师的引导下，寻求解决问题的方法。教师的追问不仅开阔了学生的视野，探究了该题的多种解法，更重要的是在师生共同探究该题的过程中，拓展了学生的思维，调动了学生学习的积极性和思考的主动性，凸显了学生的主体地位。

如果说教学是一门艺术，那么教师和学生都是艺术家，课堂则是艺术家们共同为艺术而奋斗的圣地。只要教师拥有一双善于发现的眼睛，就能在课堂收获意想不到的惊喜。面对学生的错误，教师不妨把它当作教学的原材料，以此为突破口，进行有效追问。只要教师善于抓住教学契机，课堂将真正成为师生艺术创作的天堂。

责任编辑 王 慧