液晶光学相控阵远场光强分布研究*

于 淼，郑友进，李 聪

(牡丹江师范学院超硬材料省重点实验室)

0 引言

激光雷达在人们发明了激光以后不久就已经问世［1］，但是直到现在才随着它的相关组件(尤其是激光器)技术的不断的发展而日渐成熟［2］.近些年来，液晶光学相控阵雷达受到高度的重视.液晶光学相控阵阵列作为其中的核心部件起着至关重要的作用.

1 液晶光学相控阵结构及其工作原理

1.1 液晶材料的电控双折射效应

液晶是一种各向异性的特殊物质状态，它与常见的物质状态相比其分子的性质有着巨大的差别和不同，这种差别表现在导电性能，光学性能，电磁学性能等诸多方面.液晶的使用时需要外部电场调制的，在调制电场的作用下其分子在空间上发生旋转，因而导致材料性能特别是光学能发生了变化.因此在有外加电场的作用时，它的分子发生旋转从而导致其分子的一些光学性质发生一定的变化.液晶盒内的工作物质收到外部信号调制产生一个与调制信号相应的光学性能变化，这种变化携带了调制信号的信息，当光信号照射工作介质时，得到的输出光信号在工作介质的作用下将会被调制信号所调制，引起空间光场分布的变化，综上通过调制信号的变化在液晶的作用下可以使输出光信号发生改变.图1为液晶电光效应的示意图.

图1 液晶的电光效应示意图

液晶的电光效应包括很多方面的内容，而在液晶光学相控阵中最主要利用的是液晶电光效应中的双折射效应，因此该文在此主要以液晶的双折射效应为例对液晶的电光效应予以介绍.

将调制电压施加在液晶盒的两端，液晶分子受到电压的调制，在外加电压的作用下由于发生了分子的极化，其分子方向发生一定的旋转，旋转程度随外电压大小变化而发生变化，这样就导致了其折射率的改变率的改变，这种现象称之为液晶的电控双折射效应.

液晶具有双折射效应，和其他双折射晶体一样用no和ne分别表示其分子的寻常光折射率与非寻常光折射率.这里以向列型液晶为例，如图2(a)，如果不存在外加的调制电压，液晶分子的折射率表现为非寻常光折射率.如图2(b)所示，如果将一个外加的调制电压施加在液晶分子上，液晶分子就会根据外加调制电压所携带的信息发生旋转并且旋转的方向是随着外加的调制电压的变化而发生变化的.

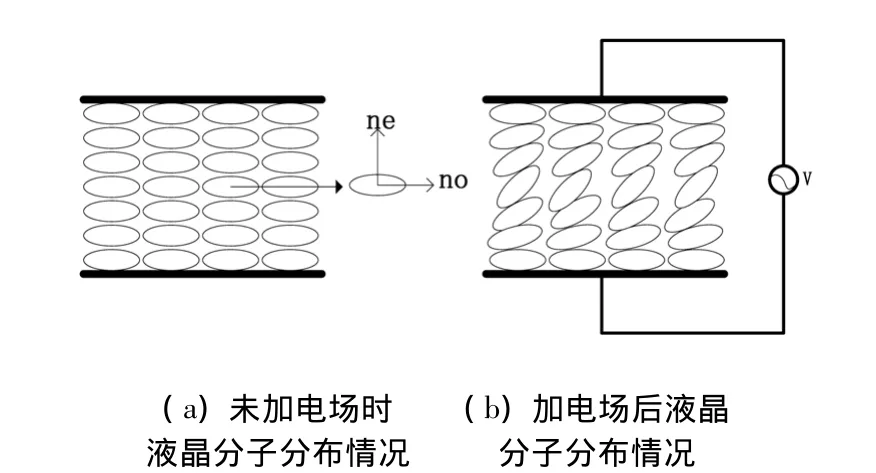
图2液晶加压偏转示意图

如果以液晶分子的中心为参考时，θ用来表示液晶分子偏离中心的角度，称为液晶分子旋转的角度，所加电压不同，θ就会发生变化，此时液晶对入射光的折射率可以用θ表示为:

液晶对入射光的折射率不同时，光束通过以后就会产生不同的相位延迟，设入射光的波长为λ，那么光束通过液晶以后所产生的相位延迟［3］:

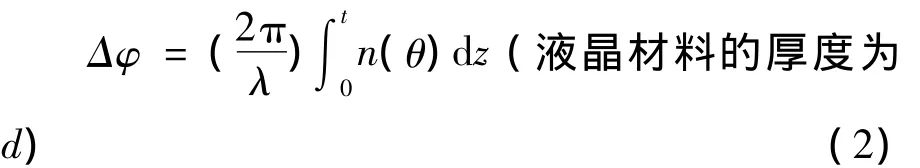
1.2 液晶相控阵阵列结构

液晶相控阵阵列结构是由两部分构成，如图3所示，一部分是由电信号调制端接入的两层透明电极组成，其主要材料是氧化铟锡(ITO)，另一部分是电极之间注入的液晶材料，起到调制光信号的作用.液晶相控阵阵列的一层电极是完整的条形电极，在其上加载基准电压;而另一层电极被分割成很多小的条形电极，液晶相控阵阵列最小的控阵单元是一个小的条形电极，每个控阵单元彼此是分立的，多个控阵单元共同完成对入射光的调制过程，这就是液晶相控阵阵列的阵列结构.

在液晶光学相控阵中的相控宽度即为电极宽度，相邻相控单元中心间距为相邻两个电极中心之间的距离，定义:占空比为相控宽度与相邻相控单元中心间距之比，设占空比用字母c来表示，其中d表示相邻相控单元中心间距，a为相邻相控单元之间的间隔，则其数学表达式可写成:

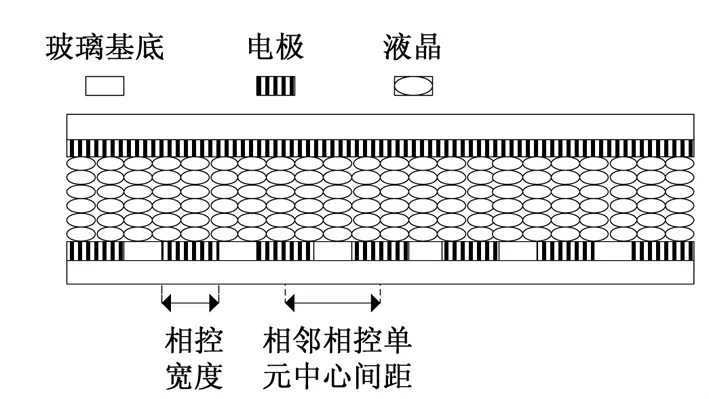
图3 液晶光学相控阵阵列结构

那么当电极之间没有间距，即当相控宽度与相邻相控单元中心间距相等时，占空比c=1;而实际中，为了保持相邻两个相控阵单元之间的绝缘，相邻控阵单元之间就一定要距离一定的间隔，此时占空比c小于1.

2 占空比小于1时液晶光学相控阵远场光强分布

瑞利－索末菲公式能够很准确的计算出远场的波束分布，计算虽然准确，但是在实际进行积分计算时存在很大的数学上的困难，该文主要研究边瓣能量问题，而不涉及到扫描角度的精度问题，因此，该文采用在瑞利–索末菲公式基础上合理近似得到夫琅禾费衍射公式对远场光束分布进行推导，对该文的研究结果没有影响.

图4 液晶相控阵阵列出射光束传输光学模型

图4为液晶光学相控阵阵列出射光束传输的光学模型.光束从左入射到液晶光学相控阵阵列上，U0(x0)为液晶阵列后表面光波振动的复振幅，右侧是远场区域，U1(x1)是远场处光波振动的复振幅，θ为光束的偏转角度，z为液晶光学相控阵后表面距离远场的距离.根据夫琅禾费衍射公式可以得到远场的复振幅:

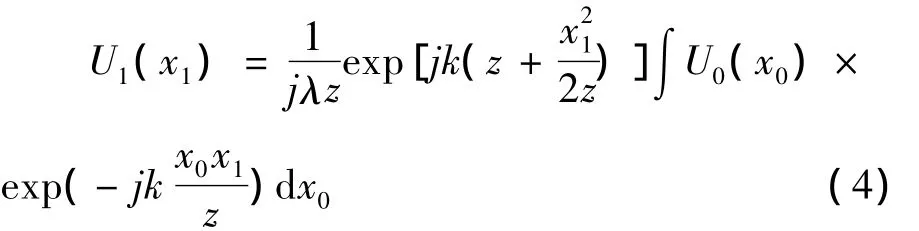
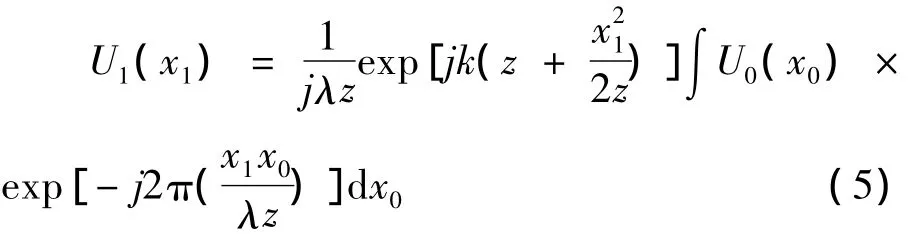
根据傅里叶变换的定义可以推出

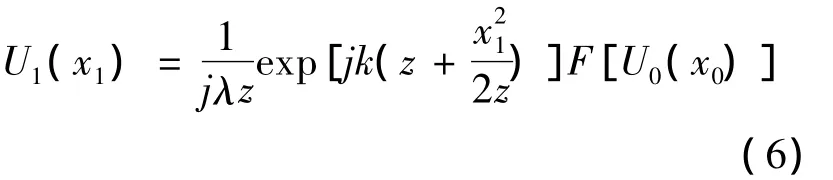
单位振幅平行光垂直照明时，液晶光学相控阵后表面复振幅与透过率函数是相等的.设透过率函数用R(x0)来表示，把式(6)改写

光强分布形式:

占空比小于1时，液晶光学相控阵出射波阵面相位分布形式如图5所示:

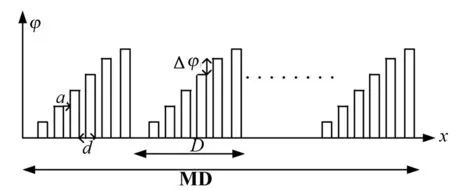
图5 考虑占空比小于1光学相控阵出射波阵面相位

考虑占空比以后液晶光学相控阵后表面出射波阵面相位分布仍然规则，因此可以写出此时液晶光学相控阵透过率函数.

一个相控阵周期的透过率函数:

式(9)中第一项为有相位延迟部分，第二项为不引起相位延迟部分，也就是间隙部分.

同样，整个液晶相控阵的透过率函数:

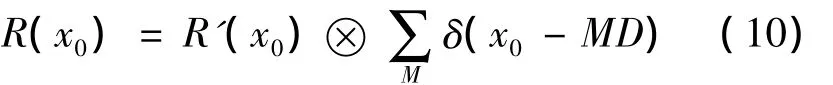
一个周期的透过率函数的傅里叶变换:

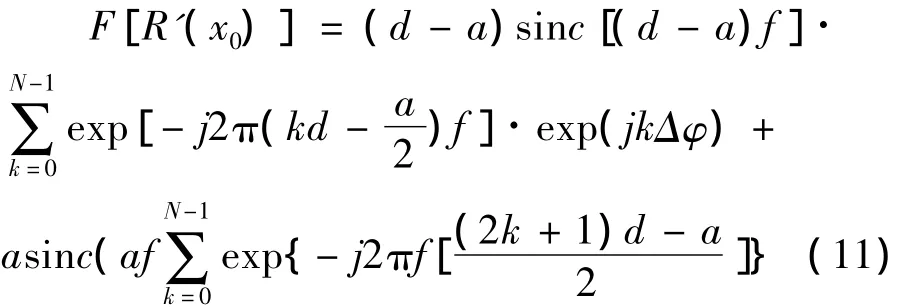
其中:

将φ =2πfd－Δφ代入得到:

根据卷积的性质，两个函数卷积的傅里叶变化等于其傅里叶变换的乘积，因此有:

根据(7)(8)两式得到远场光强分布形式:

当周期较多时，两个求和函数相互叠加可以忽略不计，因此两项大小的平方求和就可以算出总光强.

光强表达式为:

3 结束语

为了保持相邻两个相控阵单元之间的绝缘，相邻控阵单元之间就一定要距离一定的间隔，此时占空比c小于1，该文主要从夫琅禾费衍射公式入手，推导了占空比小于1的情况下远场的光强分布形式，为今后的研究提供一定的理论基础.

［1］McManamon P F，Kamerman G，Huffaker M.A history of ladar in the United States［C］.Proc SPIE，2010(7684):76840T.

［2］McManamon P F.Review of ladar:a historic，yet emerging，sensor technology with rich phenomenology［J］.Optical Engineering，2012(51):060901.

［3］Wang X，Wilson D，Muller R，et al.Liquid－crystal blazed－ grating beam deflector［J］.Applied Optics，2000，39(35):6545－6555.