天线座多柔体动力学建模与仿真分析*

胡长明，王长武，王贤宙

(南京电子技术研究所， 江苏 南京 210039)

天线座多柔体动力学建模与仿真分析*

胡长明，王长武，王贤宙

(南京电子技术研究所， 江苏 南京 210039)

天线座作为支撑天线阵面探测目标的传动机构，是机械扫描雷达的一个典型部件，其动力学响应特性直接影响天线波束的指向精度。文中基于ADAMS仿真软件，以第1类Lagrange(拉格朗日)方程为建模理论，建立了天线座多柔体系统动力学模型，分析了天线座齿轮副接触力、转动角速度、转动角加速度等动力学响应特性，并与天线座多刚体动力学模型仿真结果进行了对比分析。仿真得到的天线座动力学典型数据与试验结果基本一致，表明文中采用的多柔体系统动力学建模方法及建模过程合理。该动力学建模方法可供后续类似结构设计借鉴和参考。

天线座；多柔体动力学；动力学特性；仿真

引 言

多体系统是指由具有大范围相对运动的多个物体(刚体或柔体)组成的系统。多体系统动力学是研究多体系统动力学特性的工程应用基础学科，在航空航天[1]、机器人、车辆、复杂工程机械[2]等领域有着广泛的应用。按是否考虑物体的变形，可分为多刚体系统动力学和多柔体系统动力学。传统的天线座动态特性仿真是基于转子动力学、齿轮动力学理论进行分析的，忽略了模型中齿轮、轴系的变形，其仿真结果具有一定的局限性。而多柔体动力学仿真要考虑齿轮、轴承、轴等的柔性效应，更能真实地反映该系统的动力学特性。

本文基于ADAMS软件，以第1类Lagrange(拉格朗日)方程为主要建模理论，对某天线座进行了多柔体动力学研究，并与多刚体模型计算结果进行了对比分析。此项研究成果对优化该型天线座动态性能具有一定的指导意义。

1 柔性体动力学方程

以柔性体未变形时质心惯性坐标系中的3个笛卡尔坐标R=(xyz)T、3个欧拉角p=(Ψθφ)T以及柔性体模态坐标ζ=(ζ1,ζ2, …,ζM)T为广义坐标， 即

q=(Rpζ)T=(xyzΨθφζi,i=1, …,M)T

(1)

建立动力学方程[3]：

(2)

式中：t为时间；L为拉格朗日函数，L=T-V(T和V分别表示动能和势能)；Λ为能量耗散项；Φ为约束方程；λ为拉格朗日乘子；q为广义坐标；Q为广义力。

2 天线座动力学建模

2.1 基本假设[4]

在建立模型之前，先对模型进行规划，关注对仿真起主导作用的因素，对结果影响不大的特征要进行简化处理。本文对天线座作了如下等效处理：

1)天线座底座、横滚电机齿轮、横滚小齿轮、横滚大齿轮、横滚部分、俯仰部分、俯仰电机齿轮、俯仰小齿轮、俯仰大齿轮、上天线托架、下天线托架、方位电机齿轮、方位大齿轮和方位小齿轮作为刚体处理；

2)天线座横滚轴、横滚电机轴、横滚短轴、俯仰电机轴、俯仰短轴、方位电机轴、方位短轴作为柔体处理；

3)不考虑轴承径向间隙的影响；

4)底座固定不动。

经简化后的天线座三维模型如图1所示。

图1 天线座结构示意图

2.2 拓扑关系构建

在2.1节前提下，基于ADAMS仿真平台建立了天线座系统多柔体动力学模型，模型的各部分连体坐标系如图2所示。

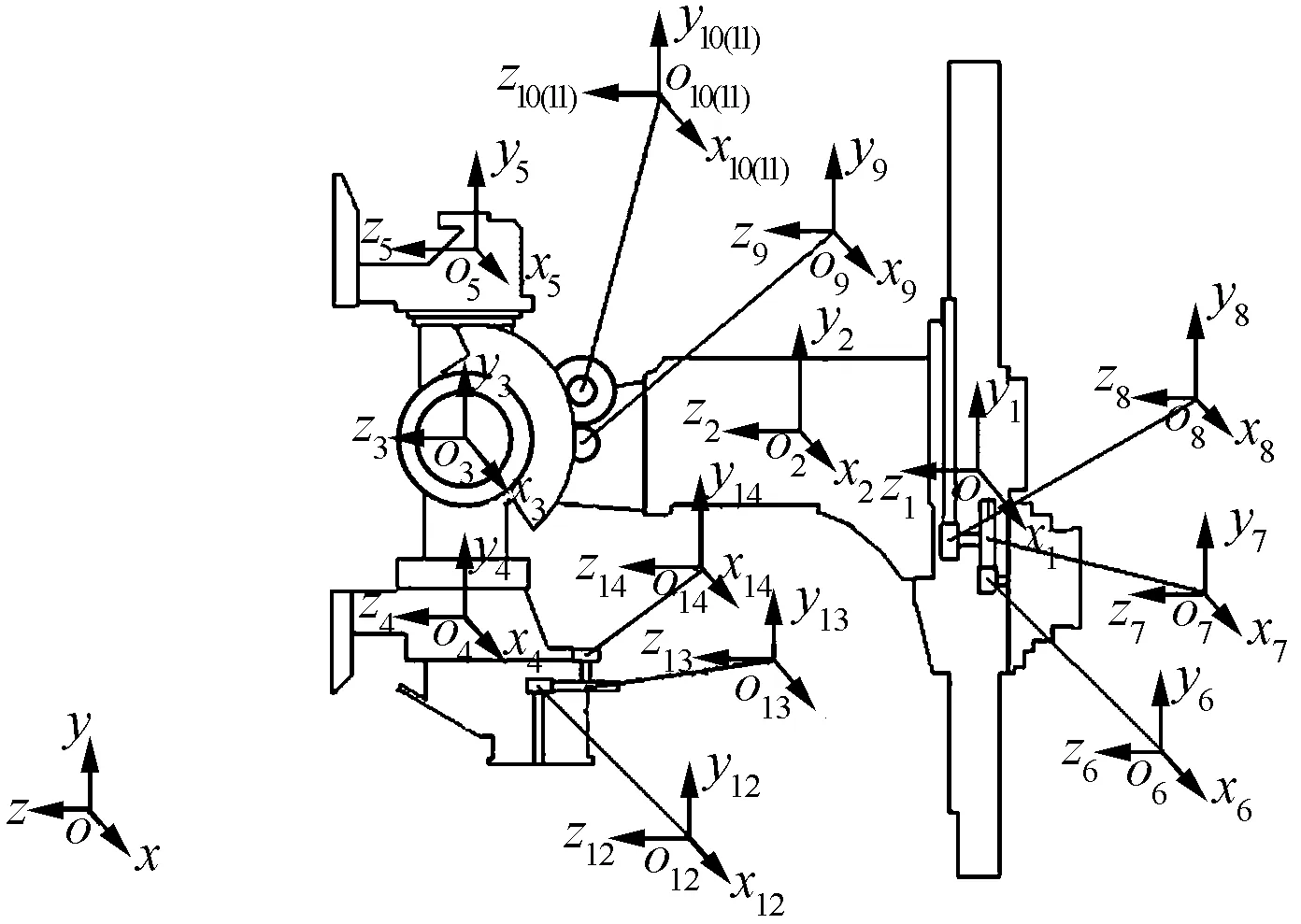
图2 天线座各部分连体系

系统的全局坐标系为o-xyz，系统拓扑关系如下：

1)底座连体系为o1-x1y1z1，以固接铰与地面相连接；横滚轴在主节点处以固结铰与底座相连接。

2)横滚部分连体系为o2-x2y2z2，在横滚轴主节点处以2个转动铰与底座相连接，绕o2z2轴转动；横滚电机齿轮连体系为o6-x6y6z6，在主节点处以固结铰与横滚电机轴相连接；横滚电机轴与底座在主节点处以2个转动铰相连接，绕o6z6轴转动；横滚大齿轮连体系为o7-x7y7z7，在主节点处以固结铰与横滚短轴相连接，横滚大齿轮与横滚电机齿轮定义为接触(横滚一级齿轮副)；横滚短轴与底座在主节点处以2个转动铰相连接，绕o7z7轴转动；横滚小齿轮连体系为o8-x8y8z8，在主节点处以固结铰与横滚短轴相连接，横滚小齿轮与横滚部分定义为接触(横滚二级齿轮副)。

3)俯仰部分连体系为o3-x3y3z3，以转动铰与横滚部分相连接，绕o3x3轴转动；俯仰电机齿轮连体系为o9-x9y9z9，在主节点处以固结铰与俯仰电机轴相连接；俯仰电机轴与俯仰部分在主节点处以2个转动铰相连接，绕o9x9轴转动；俯仰大齿轮连体系为o10-x10y10z10，在主节点处以固结铰与俯仰短轴相连接，俯仰大齿轮与俯仰电机齿轮定义为接触(俯仰一级齿轮副)；俯仰短轴与俯仰部分在主节点处以2个转动铰相连接，绕轴o10x10转动；俯仰小齿轮连体系为o11-x11y11z11，在主节点处以固结铰与俯仰短轴相连接，俯仰小齿轮与横滚部分定义为接触(俯仰二级齿轮副)。

4)方位电机齿轮连体系为o12-x12y12z12，在主节点处以固结铰与方位电机轴相连接；方位电机轴与下天线托架在主节点处以2个转动铰相连接，绕o12y12轴转动；方位大齿轮连体系为o13-x13y13z13，在主节点处以固结铰与方位短轴相连接，方位大齿轮与方位电机齿轮定义为接触(方位一级齿轮副)；方位短轴与下天线托架在主节点处以2个转动铰相连接，绕轴o13y13轴转动；方位小齿轮连体系为o14-x14y14z14，在主节点处以固结铰与方位短轴相连接，方位小齿轮与俯仰部分定义为接触(方位二级齿轮副)。

5)下天线托架连体系为o4-x4y4z4，以转动铰与俯仰部分相连接，绕o4y4轴转动；上天线托架连体系为o5-x5y5z5，以固结铰与下天线托架相连接；天线与下天线托架以固结铰相连接。

天线座多体系统共包含14个刚体、7个柔体、16个转动铰和12个固结铰，共有自由度146个。

2.3 天线座刚体建模

在I-DEAS软件中建立全局仿真坐标系o-xyz，将天线座ProE三维模型导入I-DEAS软件，并赋予天线座各部分的质量、质心、转动惯量数据等。根据天线座多体系统的拓扑关系，利用I-DEAS的Mechanical Design模块建立各个刚体模型，再利用Export命令生成ADAMS软件的.cmd文件，形成ADAMS仿真所需的刚体模型。

2.4 天线座柔体建模

根据天线座各转轴的结构特点，利用有限元分析软件I-DEAS的meshing模块对其进行网格划分，将网格划分的信息存为Universal File，再导入ADAMS/AUTO FLEX模块，形成ADAMS仿真所需的多柔体模型。

基于ADAMS/AUTO FLEX模块在转轴与轴承支撑接触的区域定义主、从节点，其中主节点位于转轴中心轴线上，柔体与刚体在各主节点处以固结铰或转动铰连接，这样可以保证主节点与各从节点在约束、载荷关系上的一致性。但由于主节点的引入，构件的模态将增加，每定义1个主节点，就将增加6个模态。

2.5 接触模型

本文采用Lankarani and Nikravesh接触力模型对经典动量平衡接触力模型进行了改进。将Lankarani and Nikravesh接触力模型写成子程序，并编译连接生成动态连接库(.dll文件)，在仿真计算过程中沿用ADAMS的接触点搜索算法，而接触力的计算则通过调用自编的子程序来实现。

接触刚度系数采用Hertz接触理论进行估算。齿轮啮合变形主要发生在接触区附近，忽略物体中的弹性波动，不计摩擦，刚体之间的接触可直接从Hertz接触理论得到。对于简单旋转刚体，有：

(3)

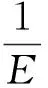
(4)

(5)

式中：P为加在物体上的载荷；ρ为综合曲率半径；E为综合弹性模量；δ为互相接触的2个物体对应点接近的距离；v1和v2分别为两物体材料的泊松比；E1和E2分别为两物体材料的弹性模量；ρ1和ρ2分别为两旋转体接触点处的当量曲率半径。

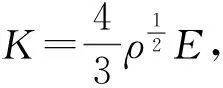
(6)

式中：d1为节圆的直径；α为分度圆压力角；α′为节圆角；u为齿数比。

3 仿真分析

3.1 多柔体模型动态响应

通过仿真，得到了天线座方位/俯仰传动轴为柔体时电机的输出力矩曲线、减速箱大小齿轮接触力曲线、转动角加速度曲线等。因篇幅有限，文中仅列出部分重点关注的仿真结果，如图3～图9所示。

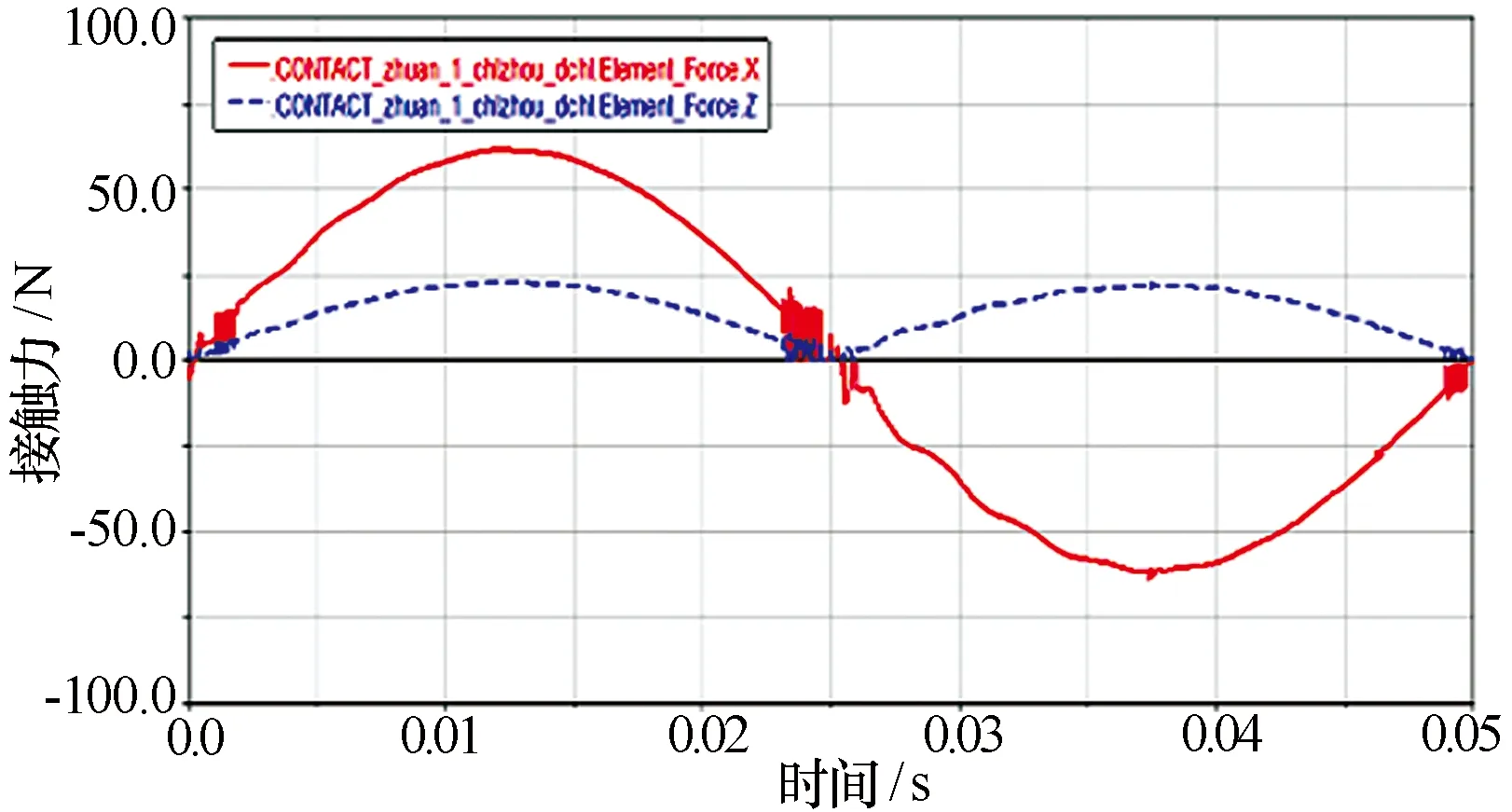
图3 方位减速箱一级齿轮副接触力曲线

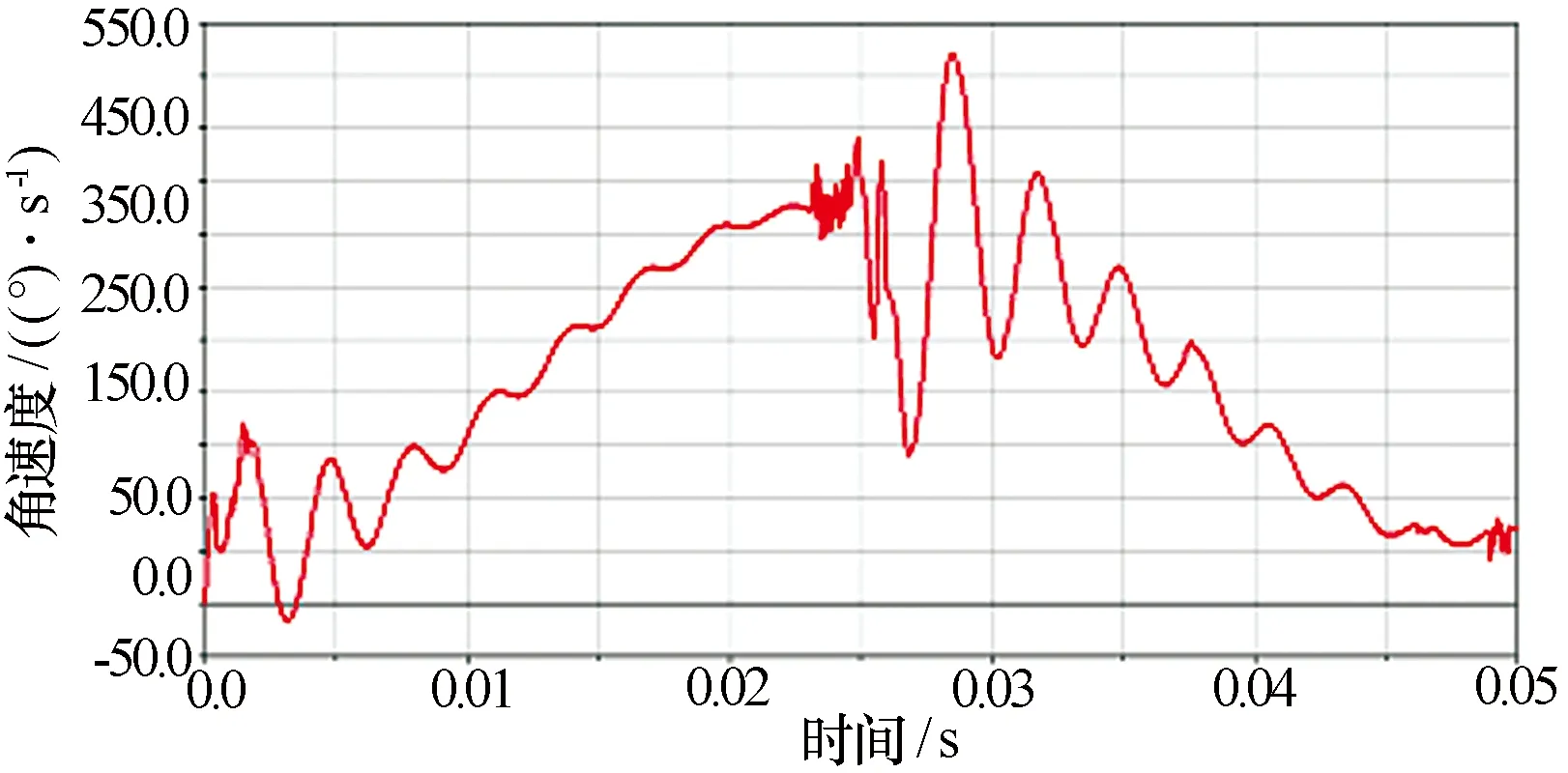
图4 方位一级小齿轮转动角速度曲线

图5 方位一级大齿轮转动角速度曲线

图6 天线方位转动角速度曲线

图7 方位一级小齿轮转动角加速度曲线

图8 方位一级大齿轮转动角加速度曲线

图9 天线方位转动角加速度曲线

从图5、图6可以看出，一级齿轮副的小齿轮和大齿轮的转速波动现象比较明显，而天线的转速基本上无波动现象。

对图7～图9进行分析发现，方位一级小齿轮和大齿轮角加速度在0 s、0.025 s和0.05 s 3个时刻附近出现明显的振荡，高频成份较多，而方位旋转体的角加速度在正弦曲线作上下小范围的波动，高频成分很少；从图3的接触碰撞力曲线亦可以看出，在相同时域内，接触碰撞力含有高频振荡成分，这是由于角加速度高频振荡的原因。对方位一级小齿轮角加速度曲线和天线方位转动角加速度曲线进行频谱分析发现：方位一级小齿轮的角加速度除在低频区有几个贡献较大的频点20 Hz、265.4 Hz、334.2 Hz外，在高频区亦存在贡献较大的几个频点4 477.9 Hz、5 279.1 Hz、8 541.9 Hz；而天线的方位转动角加速度仅在低频区有2个贡献较大的频点20 Hz、379.0 Hz。试验得到的天线方位转动角加速度谱线如图10所示。从图10可知，天线座在20 Hz附近有明显的谐振点，与仿真结果基本一致。

图10 由试验得到的天线方位角速度响应曲线

3.2 多刚体模型动态响应

同样，对天线座方位/俯仰传动轴等效为刚体时进行了仿真计算，2种计算模型得到的天线座方位一级传动小齿轮和大齿轮的角速度曲线和角加速度曲线有一定的区别，但总体趋势基本一致，如图11～图17所示。

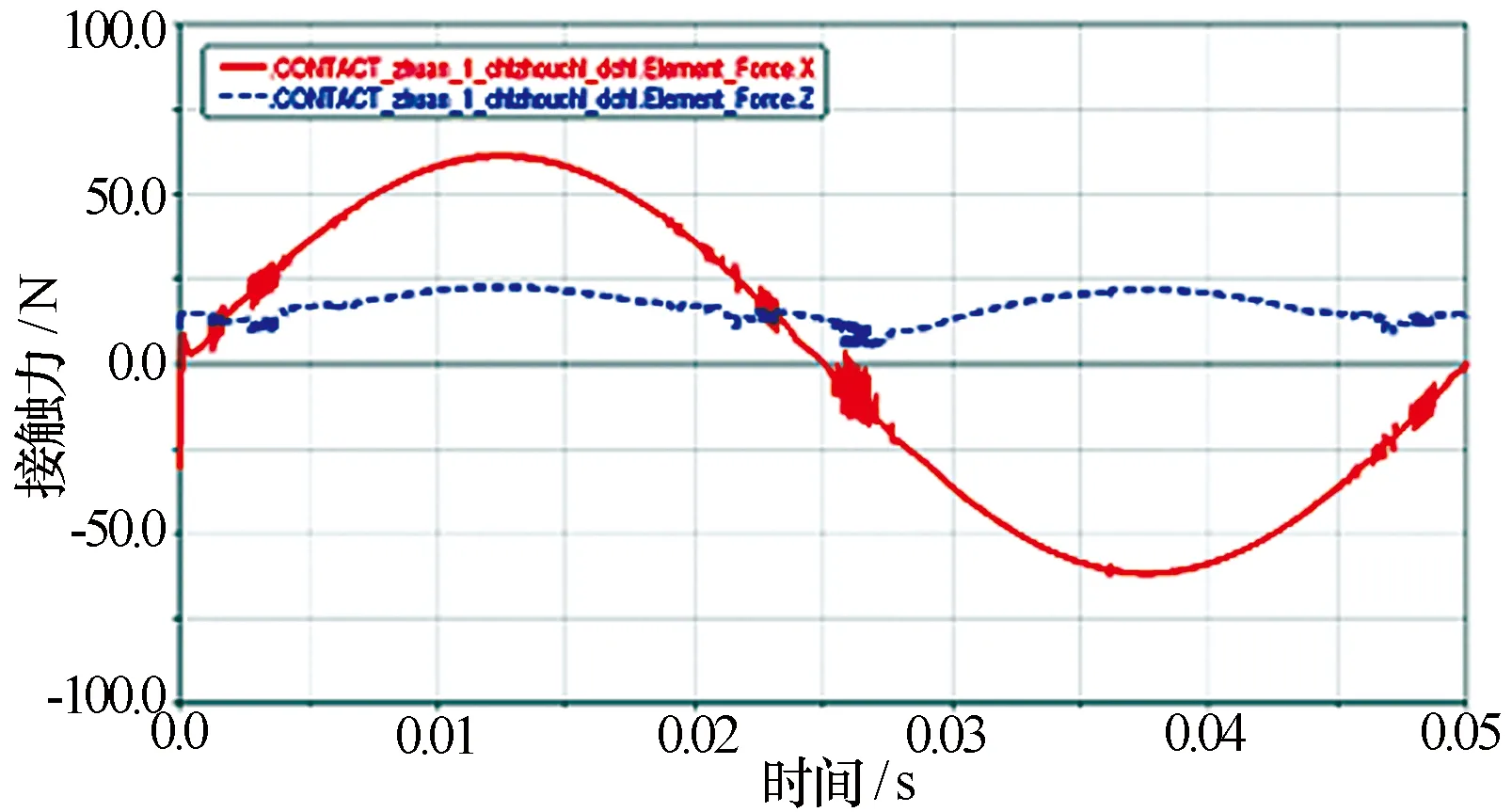
图11 方位减速箱一级齿轮副接触力曲线

图12 方位一级小齿轮转动角速度曲线

图13 方位一级大齿轮转动角速度曲线

图14 天线方位转动角速度曲线

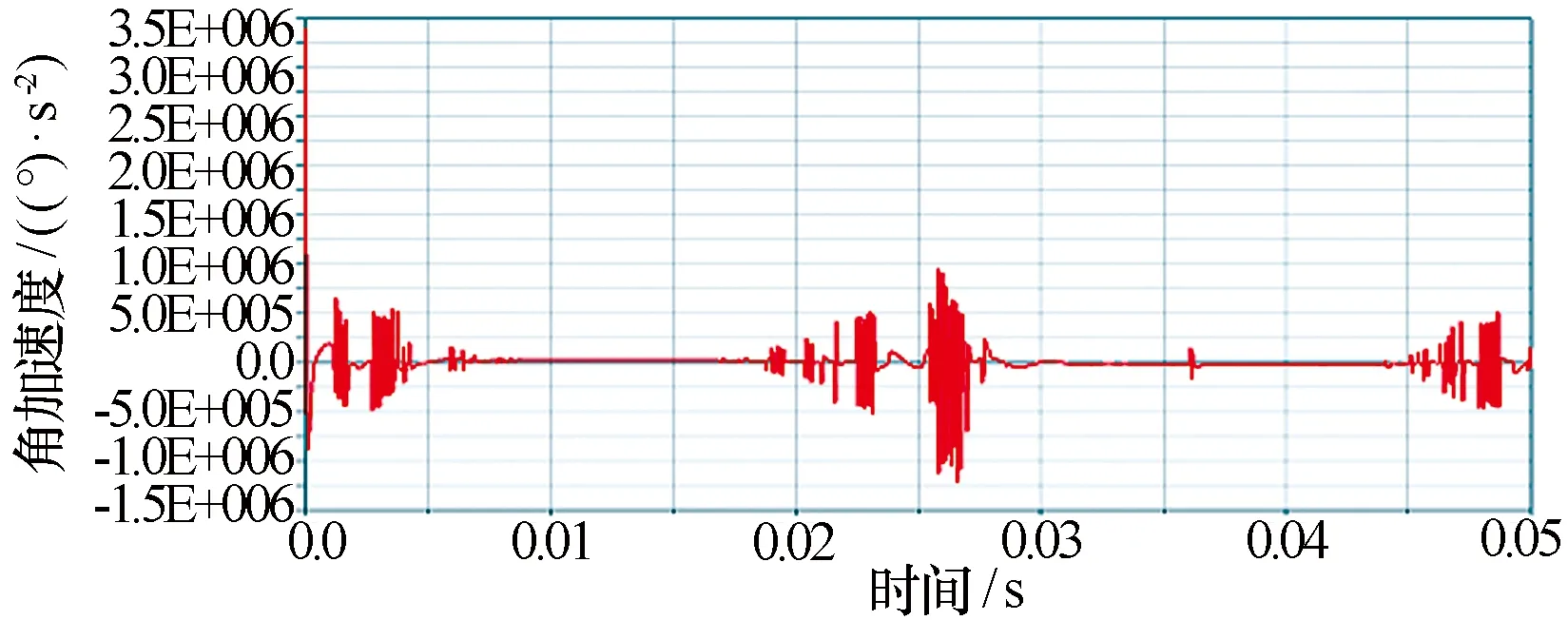
图15 方位一级小齿轮转动角加速度曲线

图16 方位一级大齿轮转动角加速度曲线

图17 天线方位转动角加速度曲线

3.3 对比分析

对比多柔体和多刚体动力学模型仿真结果，可得出如下结论：

1)2种模型仿真得出天线座方位一级传动小齿轮和大齿轮的角速度/角加速度有一定的区别，但总体变化趋势一致，2种模型得到的天线方位转动角速率曲线几乎无差异；

2)多柔体模型仿真得出天线座方位角速度最大贡献频率比多刚体模型略低0.5 Hz，最大贡献频率比实际激励输入频率略大；

3)方位一级齿轮副在0 s、0.025 s和0.05 s 3个时刻仍含小量级的高频振荡，其主要原因是方位旋转体的转动惯量远大于一级齿轮副的转动惯量。当然，如果考虑齿轮的侧隙、传动误差、时变刚度以及与轴承的耦合(轴承径向间隙、径向大刚度)等原因，齿轮的传动特性会更加复杂，这将在后续研究中作进一步探讨。

多柔体和多刚体动力学模型仿真结果对比如图18～图21所示。

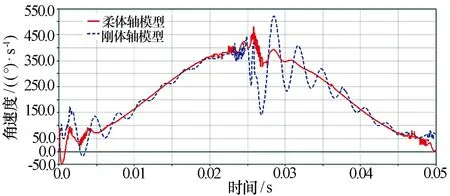
图18 方位一级小齿轮转动角速度对比

图19 方位一级大齿轮转动角速度对比

图20 天线转动角速度对比

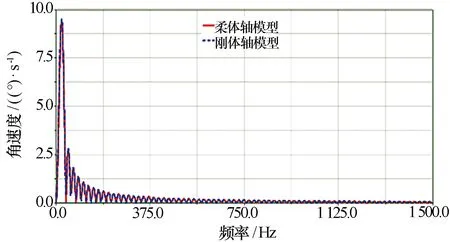
图21 天线转动角速度频谱对比

4 结束语

仿真结果显示，考虑了非线性的天线座多柔体系统动力学模型计算出的方位向谐振频率为20 ～21 Hz，与试验实测结果较为接近，表明本文考虑接触等多种非线性因素的多柔体系统动力学建模方法可行。文中的分析模型未考虑轴承自身对天线座动力学的影响，其仿真结果还存在一定的局限性。下一步将考虑建立含柔性轴承的天线座动力学模型，并对影响天线座动力学特性的结构参数进行灵敏度仿真。

[1] 平丽浩, 王长武. 大规模接触转台系统动力学建模与仿真[J]. 机械工程学报, 2007, 20(4): 369 -373.

[2] 马星国, 陆扬, 尤小梅. 基于多柔体动力学技术的行星轮系多体动力学仿真分析[J]. 中国机械工程, 2009, 20(16): 1956 -1964.

[3] 何玉林, 黄伟, 李成武, 等. 大型风力发电机传动链多柔体动力学建模与仿真分析[J]. 机械工程学报, 2014, 50(1): 61- 69.

[4] 吴凤高. 天线座结构设计[M]. 西安: 西北电讯工程学院出版社, 1986.

胡长明(1969-)，男，研究员级高级工程师，主要从事雷达结构总体设计和技术管理工作。

王长武(1973-)，男，博士，研究员级高级工程师，主要从事雷达结构总体设计工作。

王贤宙(1982-)，男，硕士，高级工程师，主要从事雷达结构总体设计工作。

Flexible Multi-body Dynamics Modeling and Simulation Analysis of Antenna Pedestal

HU Chang-ming，WANG Chang-wu，WANG Xian-zhou

(NanjingResearchInstituteofElectronicsTechnology,Nanjing210039,China)

The antenna pedestal, as the transmission mechanism to support the antenna array, is a typical part of mechanic scanning radar. The dynamic characteristics of the antenna pedestal determine the pointing accuracy of the antenna beam. In this paper, with the 1st Lagrange function as the modeling theory, the flexible multi-body dynamics model of the antenna pedestal is built based on ADAMS software. The dynamic characteristics of the antenna pedestal are analyzed including the contact force, the angular velocity and the angular acceleration of the internal gear pair and compared with the simulation results of the rigid multi-body dynamics model. The simulation results are in agreement with the experimental results, which shows that the flexible multi-body dynamics modeling method is feasible and reasonable. This simulation method can provide excellent reference for structure design of the similar transmission mechanism.

antenna pedestal; flexible multi-body dynamics; dynamic characteristics; simulation

2015-08-20

TP391.9；TN820.8+2

A

1008-5300(2015)05-0052-06