突出三大主体栏目 彰显教材编写特色

周茂生+姜向阳

新修订的青岛版《义务教育教科书·数学》九（上），于2014年9月和大家见面了.新版教科书除在知识内容上有较大的变化外，编写特色更加鲜明.其一，本册教科书的编排结构自然、和谐、合理，体现了螺旋式上升递进的编写原则.栏目设置更加新颖灵活，图文并茂，生动活泼有趣，具有启迪性、探究性，不仅加强了让学生动手操作和探究归纳能力的培养，而且更加体现了知识的形成过程，与其它版本的教科书相比，更具人性化.其二，根据教学需要，本册教科书设置了大量的“观察与思考”、“交流与发现”、“实验与探究”等进行数学活动的三大主体栏目.通过真实的情境，鲜活的事例或数学自身的素材，帮助学生轻松步入学习佳境，在观察、实验、思考、猜想、验证、推理与交流等数学活动中，让学生亲历数学知识的发现与探究过程，使学生真正成为学习的主人.正如教育部教材审查委员会给出的评价：教科书设计了“观察与思考”、“实验与探究”、“交流与发现”等特色栏目，能积极鼓励学生自主探索发现，感受数学源于生活、应用于生活，更加注重了能力培养.

下面通过几则案例来说明如何利用新教材特色栏目实施数学有效教学的.

1 观察与思考

观察与思考栏目是通过真实的情境和鲜活的实例，或提出富有启发和思考性的问题，帮助学生进入自主学习、观察猜想、实验验证等的学习情境，切实能引导学生深入进去解决问题.对于运算定律、公式、法则等知识的学习，是从学生已有的认知发展水平和已有的经验出发，遵循“由特殊到一般”的规律，结合具体的学习内容，用观察与思考栏目提出一些问题，引导学生围绕问题进行观察、分析、综合、推理、判断等思维活动，在活动的过程中经历获得知识的过程，从而得到有关的结论.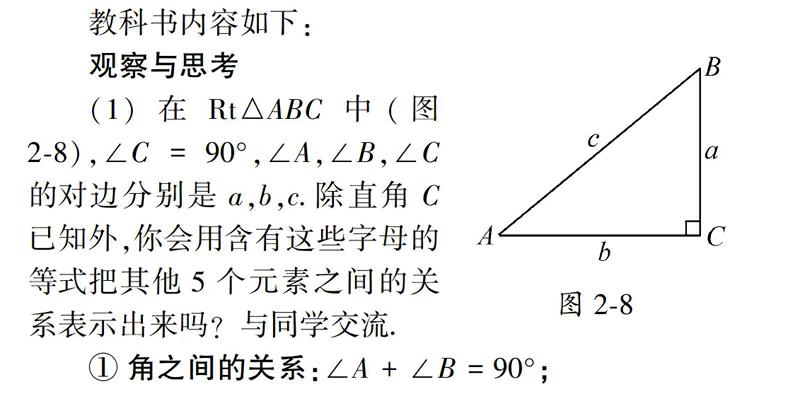

案例1 “2.4直角三角形的解法”观察与思考过程（九（上）教科书第49页）：

教科书内容如下：

（1）在Rt△ABC中（图28），∠C=90°，∠A，∠B，∠C的对边分别是a，b，c.除直角C已知外，你会用含有这些字母的等式把其他5个元素之间的关系表示出来吗？与同学交流.

①角之间的关系：∠A+∠B=90°；

②边之间的关系：a2+b2=c2；

③角与边之间的关系：sinA=ac，cosA=bc，tanA=ab.

（2）观察上面的三组等式，你发现在直角三角形中，除直角以外，至少知道几个元素就可以求出其他的未知元素？

教科书卡通形象小博士温馨点拨：

除直角以外，如果再知道直角三角形的两个元素（至少一个是边），就可以求其他的元素了.

笔者利用教科书本节内容是这样引导学生观察与思考的：

师：根据图28，观察上面的三组等式，你发现了什么？

师：在直角三角形的六个元素中，除直角外，还有几个元素？

生：五个元素.

师：在直角三角形中，除直角外，还需知道几个元素就可以求出其他的未知元素？

生：除直角外，如果再知道直角三角形的两个元素，就可以求其他的元素了.

师：在教科书所列出的②、③两组等式中，每个等式中都含有三个量，如果已知其中的两个量，如何求出第三个量？

生：运用勾股定理和锐角三角比可以求出第三个量.

师：如果已知的其中的两个量都是角，能否求出其他的未知的量？

生：不能.因为等式②中，三个量都是边，等式③中的三个量有一个是角，另外两个量都是边，因而在已知的两个元素中，至少须有一个量是边才能求出其他的未知的量.

师：好！在直角三角形中，除直角外，如果再知道直角三角形的两个元素（至少一个是边）就可以求出其他的元素了.

从上述学生的思考与交流可以看出，学生通过阅读教科书给出的观察与思考栏目，在观察图形、回忆已学过的知识的基础上，对直角三角形中角与角之间（两锐角互余）、边与边之间（勾股定理）、角与边之间（锐角三角比）的关系进行了梳理和总结，较好地理解了在直角三角形中，除直角外，知道其中的两个元素（至少一个是边），就可以求出其他三个未知元素.

2 交流与发现

交流与发现栏目是在关注情境的设置、问题的提出以及讨论交流的前提、方式、时间处理等因素下，让学生明确做什么，思考什么，在此基础上再引导学生进行交流的.在给出一些基本的数学概念之前往往会结合具体的学习内容，用交流与发现栏目，提出一系列的问题，用这些问题引导学生去主动地、富有个性地学习，不断地提高学生发现问题和提出问题的能力.对于有些定理、性质的学习，本教科书也是采用交流与发现栏目，提出一系列的问题，引导学生通过解答这些问题，发现定理和性质的.

案例2 “1.1相似形”概念的发现与建立过程（九（上）教科书第4页）：

教科书内容如下：

交流与发现

图11五星红旗是中华人民共和国的国旗，国旗上的左上角有五颗五角星（图11），这五颗五角星的形状相同吗？

在现实生活中，你还见过形状相同但大小未必相等的图形吗？

形状相同的平面图形叫做相似形（similar figures）.

全等形与相似形有什么关系呢？

教科书卡通形象小亮温馨提示：

两个全等形也是相似形.