柔性针在有障碍环境中的穿刺路径规划

周 丽，康剑灵，詹 洁，冯金阳

(东华大学 理学院，上海 201620)

柔性针在有障碍环境中的穿刺路径规划

周 丽，康剑灵，詹 洁，冯金阳

(东华大学 理学院，上海 201620)

斜尖柔性针相对组织有足够的柔性，能够穿刺出弧线轨迹，且能到达传统钢针不能到达的敏感区域. 在二维有障碍环境中，通过作图找到能够避开障碍的最优路径；在三维有障碍环境中，利用快速搜索随机树法找到所有可行路径，再利用优化目标函数找到能避开障碍的最优路径. 仿真结果表明这两种路径规划均能找到最优路径，验证了规划方法的有效性.

柔性针；路径规划；快速搜索随机树

微创医疗是近年来外科临床医学迅速发展起来的一门新技术，被广泛应用于活体组织病理检查、局部组织药物投送等手术.与传统手术的穿刺钢针不同，斜尖柔性针[1](简称“柔性针”)相对组织具有足够的柔性，可利用针轴的弯曲刺出不同的轨迹，同时能避开神经、血管等障碍，灵活准确地到达传统钢针达不到的靶点位置. 美国约翰斯霍普金斯大学的Webster等人在2004年最早提出柔性针概念，由于柔性针的路径规划研究是运动控制的基础，对于准确穿刺具有重要意义，因而成为当前国内外研究的热点.

按照应用场合的不同，柔性针路径规划可分为二维路径规划和三维路径规划；按算法柔性针路径规划大体可分为数值法、搜索法和反解法，其中，数值法是通过计算目标函数的最值得到最优路径的方法，搜索法是根据路径形式特点，利用计算机的人工智能搜索算法来搜索可行路径，反解法是利用运动学反解来计算从入针点到靶点的可行路径.

文献[2]首次对柔性针进行二维路径规划，而文献[3]首次把柔性针路径规划研究扩展到三维空间，后来又扩展到三维有障碍环境，文献[4]采用DR(不同曲率的圆弧)混合型路径对三维障碍环境进行规划，文献[5]采用R/S+L(多段定曲率的圆弧及直线)型混合路径规划二维障碍环境的路径，文献[6]利用穿刺针、靶向目标与障碍物间的切线提出一种S(多段圆弧)型双弧线障碍物规避路径规划算法，文献[7]在三维有障碍环境中对柔性针穿刺进行螺旋形路径规划.

本文在刚性组织假设前提下，不考虑组织形变、针的变形等因素，首先讨论柔性针在二维有障碍环境下的路径规划问题，利用入针点、障碍物及目标点之间的位置关系，分别过入针点、目标点做障碍圆的切线，提出一种R(弧线)型路径规划算法. 其次讨论在三维有障碍环境下的路径规划问题，利用快速搜索随机树法[8]搜索可行路径，考虑针尖偏差与路径长度这两个因素，建立优化目标函数. 讨论了优化目标函数中不同的权重值对应的最优路径情况，如考虑手术中对组织的破坏性小这一因素，可选取针尖偏差尽可能大，从而减少穿刺时发生的碰撞造成对组织的破坏；若考虑减轻患者疼痛，可选取穿刺路径长度尽可能短这一因素作为主要影响因素，通过选取合适的权重值找到最优路径. 最后通过增大障碍球的半径进行障碍物规避.

1 柔性针运动学模型及穿刺路径特点

1.1 运动学模型

柔性针相对组织具有足够的柔性，穿刺时针轴受到组织的侧向力会发生弯曲，穿刺出弧线轨迹. 柔性针一般有两个自由度：一个是进给运动，实现针的穿刺；一个是自转运动，改变针尖穿刺和针轴弯曲的方向.柔性针的运动形式近似看成一台单轮车，如图1所示，其中,u1为穿刺时的进给速度，u2为穿刺的自转速度,r为穿刺时的圆弧半径，ωx为穿刺时针尖沿x轴正向产生的角速度驱动，且ωx=u1/r.

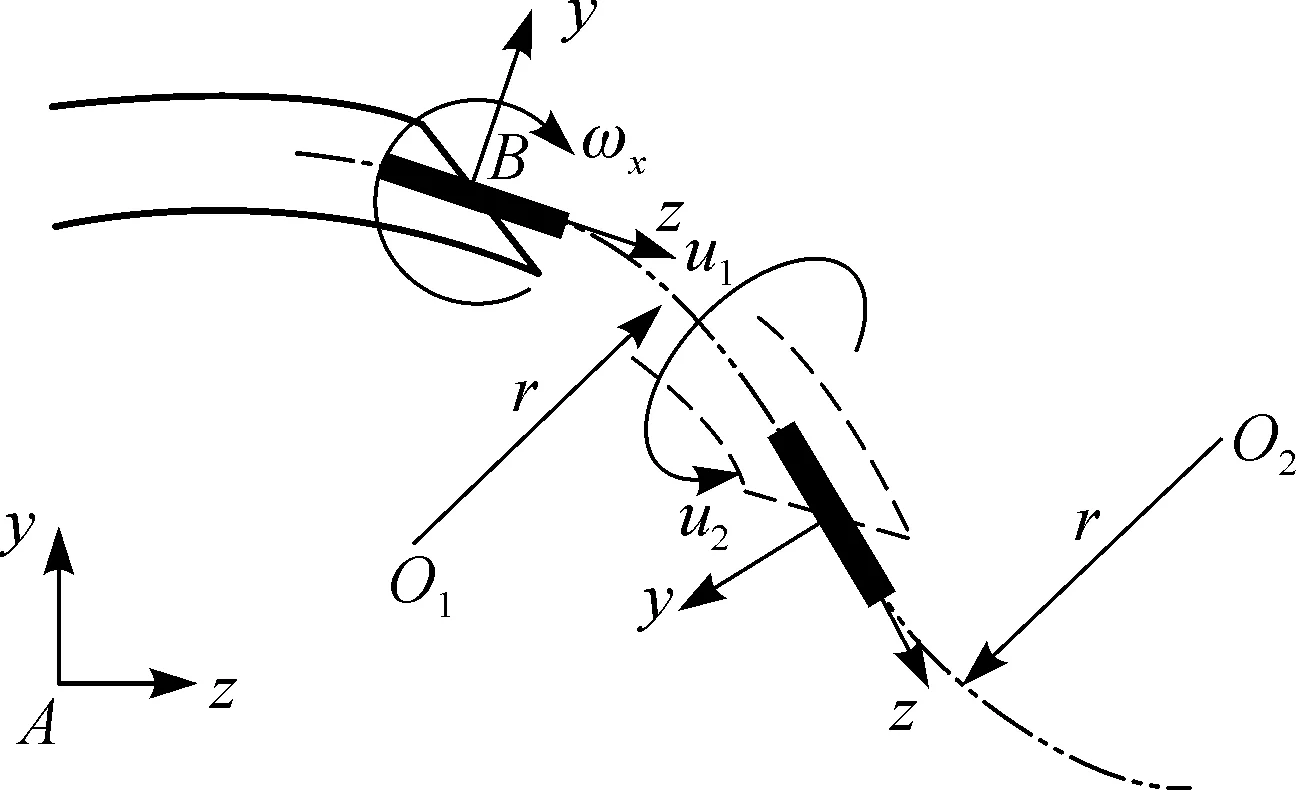
图1 单轮车运动学模型Fig.1 Unicycle kinematic model

在世界坐标系A下，单轮车轴与针尖固联，坐标系B与单轮车轴固联,z轴沿轴线指向运动方向,y轴指向弯曲圆弧的外法线方向，由右手定则可判断x轴方向.

1.2 穿刺路径特点

柔性针在进给运动和自转运动的协调控制下可以实现一定的空间位置和姿态，穿刺出独特的路径. 本文的路径规划问题研究中，假定组织是刚性的，忽略由于柔性针的刺入对组织环境的影响. 在解决二维路径规划之前，为了说明问题，首先给出控制度的概念.

控制度N：整个路径规划中需要控制不同路径形式的次数，即包含的直线或圆弧的段数.表1给出不同控制度下可能的路径形式.

表1 不同控制度下的路径形式Table 1 Different path forms under different control degrees

本文在有障碍二维环境中仅讨论控制度为1的路径规划方法，即临床上最易实现的R型路径规划.

2 柔性针穿刺路径规划

2.1 二维有障碍环境的路径规划

在二维有障碍环境中，首先确定初始入针点和目标点的位置，设定障碍，路径规划如图2所示,P1和P2两点分别是从入针点和目标点向障碍圆所作切线的交点，求出过入针点、P1(或P2)和目标点的圆的轨迹，此轨迹从入针点出发能够到达目标点且能避开障碍，从而得出两条R型轨迹作为最终可行路径.

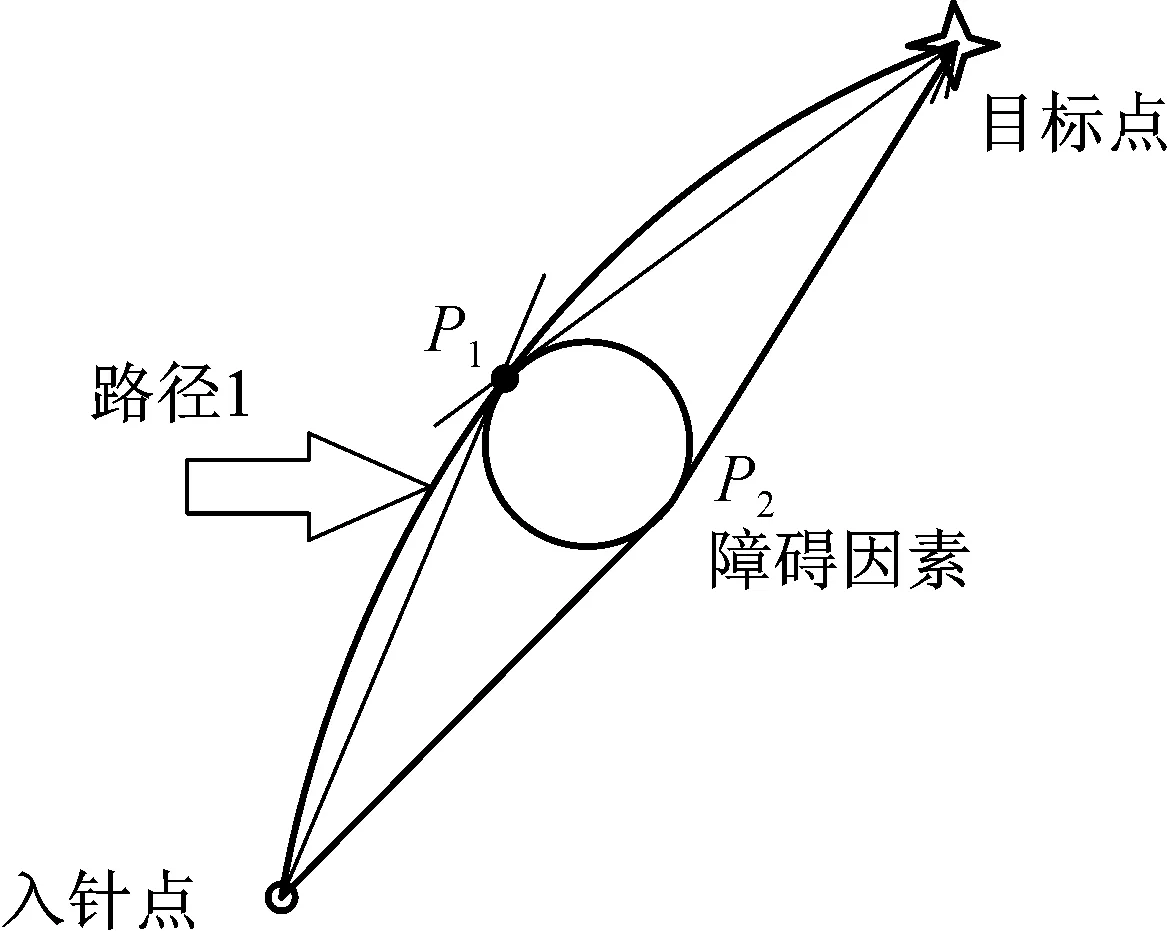
图2 路径规划简图

由于实际穿刺手术中障碍组织更复杂，所以这里设定两个圆形障碍，障碍1是以坐标(7,9)为圆心、2为半径的圆，障碍2是以坐标(14,10)为圆心、1.6为半径的圆，入针点坐标为(0,0)，目标点坐标为(20,22). 按照上述路径规划思想，利用Matlab求解计算并作图，主要步骤如下：

(1) 在平面直角坐标系中画出障碍圆1和障碍圆2的图像以及入针点和目标点的位置；

(2) 分别计算过入针点到障碍圆1的两条切线方程并在坐标系中作出切线图，计算目标点到障碍圆1的两条切线方程并在坐标系中作出切线图，记过入针点与障碍圆1的切线和过目标点与障碍圆1的切线交点分别为P1和P2，如图3所示；

(3) 计算P1和P2的坐标，分别求出过入针点、P1(或P2)、目标点的劣弧长度；

(4) 按照步骤(2)和(3)，同理作出过入针点到障碍圆2的两条切线，以及目标点到障碍圆2的两条切线并作图，记过入针点与障碍圆2的切线和过目标点与障碍圆2的切线交点分别为P3和P4，如图4所示；

(5) 计算P3和P4的坐标，分别求出过入针点、P3(或P4)、目标点的劣弧长度.

通过计算整理得出表2所示的过入针点坐标(0,0)、切线交点Pi(i=1,2,3,4)、目标点坐标(20,22)的轨迹.

表2 过入针点和目标点的4条可行轨迹Table 2 Four feasible paths connecting initial point and target point

由于柔性针在R型路径规划中有最小半径的限制，这里假定R型轨迹最小半径为50，则表2中满足条件的只有轨迹R2和R3，又通过弧长判断，弧长稍短的轨迹R2为控制度为1时的最优路径.图5是4条可行路径与障碍物的位置关系图.

2.2 基于快速搜索随机树法的三维路径规划

在三维有障碍环境中，假定入针点坐标为(0,0,0)，目标点坐标为(0,0,10)，障碍分别以坐标(-0.5,0.5,2)、(0,0.5,5)、(0.7,0.1,7)为球心，半径均为1的球体. 柔性针在三维环境中的路径规划问题，即为找到从入针点到目标点且能避开障碍的可行路径. 在三维环境中利用快速搜索随机树法找到可行路径，快速搜索随机树法(RRTs)的思想：

给定初始位形qinit和目标区域Qgoal(包含目标)，在初始位形qinit的周围取随机位形qrand，记其中距离Qgoal最近的qrand将其表示为qnear，若qnear与障碍物发生碰撞，则放弃生长，重新选取qnear，否则将qnear加入树，再从qnear周围选取新的随机位形qrand，如此重复至最新的qnear在Qgoal的范围内，即找到可行路径. 通过Matlab仿真得到如图6所示的三维有障碍环境中的可行路径.

为了在可行路径中找到最优路径，一方面使得穿刺路径最短(即对组织破坏性小、减少疼痛)，另一方面针尖距离障碍的间隙尽可能的大(防止因针的变形使得针与障碍发生碰撞)，建立如下优化目标函数[4]：

其中：Jο为针尖与最近障碍之间的距离；αl和α0为权重；T为柔性针穿刺时间. 通过选取适当的权重αl和α0，使得上述优化目标函数值达到最小，即达到最优路径.

通过RRTs搜索到一系列可行路径，随机选取可行路径当中的5条路径，计算出路径长度∑li和针尖与最近障碍的距离和∑Jο的结果如表3所示.

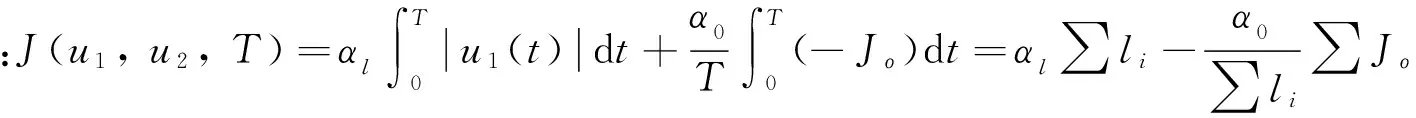
选取不同的权重值αl和α0，计算相应5条路径的目标函数值，如表4所示，其中Ji(i=1,2,3,4,5)为5种不同路径的目标函数值.

表4 不同权重值对应的目标函数值Table 4 The goal function value under different weights

由表4可知，若取αl=1.0,α0=0，即只考虑最短路径，不考虑路径与障碍之间的距离，此时第5条路径对应的目标函数值最小，即第5条路径为最优路径；若取αl=0,α0=1.0，即只考虑针尖与障碍之间的距离，不考虑最短路径，此时第3条路径对应的目标函数值最小，即第3条路径为最优路径；分析上述5种路径在不同权重值下的目标函数值，只有第3条路径在前面9种不同权重值的条件下，对应的目标函数值均最小，即总体而言第3条路径较优.

在某些实际问题中，考虑到柔性针在穿刺过程中可能会发生变形等情况，这样易使针尖与障碍物发生碰撞.为了避免这种情况的发生，在利用RRTs搜索可行路径时，把上述半径为1的小球，用半径为1.5的球来回避(在实际情况下，可以根据各个组织不同的敏感性，设定不同的回避距离)，这样可使可行路径能够远离障碍物避免与其发生碰撞.

同样如上述的三维有障碍路径规划实例，入针点与目标点坐标不变，只是将球形障碍的半径变为1.5，其他条件相同，利用Matlab仿真搜索一系列可行路径如图7所示.

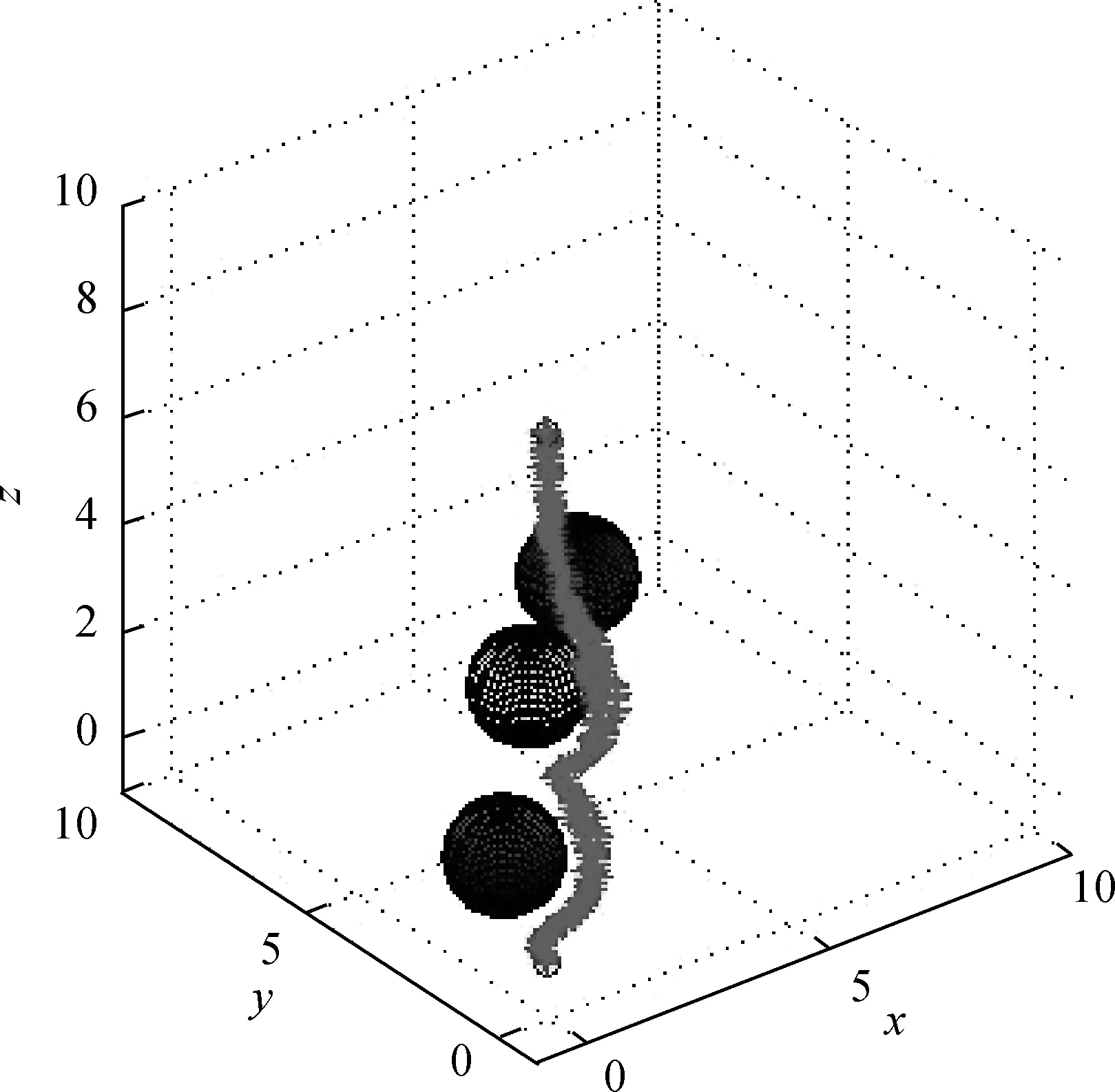
图7 三维有障碍环境中考虑障碍规避的可行路径Fig.7 Feasible paths in 3D environment while considering the avoidance of obstacles

从可行路径中随机选取5条路径，计算出路径长度∑li和针尖与最近障碍的距离和∑Jο的结果如表5所示. 将球形障碍的半径增大后即已经考虑远离障碍物的情况，只需考虑路径长度，由表5可知，路径5对应的路径长度最短，即路径5为最优路径.

表5 可行轨迹的路径长度及与障碍之间的距离 Table 5 The distance of the feasible paths and the clearance from the obstacles

3 结 语

本文研究了柔性针在有障碍二维和三维环境中的路径规划问题.二维环境中通过入针点和目标点向障碍圆作切线并计算切线交点，找到能够避开障碍的最优路径；三维环境中利用快速搜索随机树法找到从入针点到目标点且能避开障碍的可行路径，再建立优化目标函数，考虑针尖偏差与路径长度这两个因素，通过权重值分析找到符合要求的最优路径. 仿真结果表明，这两种规划方法有效可行. 今后的研究中可以考虑组织形变等因素，以及在优化目标函数的建立时增加更多影响因素，从而提高穿刺精度.

[1] WEBSTER ш R J,KIM J S,COWAN N J,et al. Nonholonomic modeling of needle steering [J]. The International Journal of Robotics Research,2006,25(5/6): 509-525.

[2] ALTEROVITZ R,GOLDBERG K， OKAMURA A. Planning for steering bevel-tip needle insertion through 2D soft tissue with obstacles [C] // IEEE International Conference on Robotics and Automation. Piscataway,NJ,USA: IEEE,2005: 1652-1657.

[3] PARK W,KIM J S,ZHOU Y,et al. Diffusion-based motion planning for a nonholonomic flexible needle model [C] // IEEE International Conference on Robotics and Automation. Piscataway,NJ,USA: IEEE,2005: 4600-4605.

[4] PATIL S,ALTEROVITZ R. Interactivemotion planning for steerable needles in 3D environments with obstacles [C] // IEEE International Conference on Robotics and Automation. Piscataway,NJ,USA: IEEE,2010: 893-899.

[5] 张永德，赵燕江，陈浩.斜尖柔性针在软组织中的二维路径规划[J].机器人,2011,33(6):750-757.

[6] 胡晓彤，曾超.靶向穿刺自动进针障碍物规避路径规划的研究[C] // 图像图形技术研究与应用.2010:181-186.

[7] DUINDAM V,ALTEROVITZ R,SASTRY S,et al. Screw-baed motion planning for bevel-tip needles in 3D environments with obstacles [C] // IEEE International Conference on Robotics and Automation. Piscataway,NJ USA: IEEE,2008: 2483-2488.

[8] KUFFNER J J,LAVALLE S M. RRT-connect: An efficient approach to single-query path planning [C] // IEEE International Conference on Robotics and Automation. San Francisco,CA,2000: 995-1001.

Path Planning of Flexible Needles in the Environment with Obstacles

ZHOULi,KANGJian-ling,ZHANJie,FENGJin-yang

(College of Science,Donghua University,Shanghai 201620,China)

Flexible bevel-tip needles could move along curved trajectories within tissue,and could reach previously inaccessible targets while maneuvering around sensitive or impenetrable areas. In 2D environment with obstacles,an optimal path while avoiding obstacles was proposed by analysing and figuring. In 3D environment with obstacles,based on the Rapidly-Exploring Random Trees (RRTs) method,a set of feasible paths were found,then an optimal path which could avoid obstacles by minimizing the optimization criterion was given. Simulation results show that both of the two path planning methods could find the optimal paths,which validate the effectiveness of the path planning methods.

flexible needles； path planning； rapidly-exploring random trees

1671-0444(2015)01-0130-05

2013-10-29

国家自然科学基金资助项目(61104125)；上海曙光计划资助项目(07SG38)；中央高校科研业务经费资助项目(11D10911)

周 丽(1989—)，女，安徽安庆人，硕士研究生，研究方向为几何控制理论.E-mail: lz7572@163.com

康剑灵(联系人)，女，副教授，E-mail: kangjl@dhu.edu.cn

O 221.3

A