考虑侧向挤出效应的软弱夹层极限荷载研究

殷　勇

(1． 中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州221008;2． 盐城工学院土木工程学院，江苏盐城224051)

考虑侧向挤出效应的软弱夹层极限荷载研究

殷勇1,2

(1． 中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州221008;2． 盐城工学院土木工程学院，江苏盐城224051)

软弱夹层构造在沿海地区工程建设中经常遇到，因其力学性能较低，易给工程的后续稳定性带来危害。目前针对软弱夹层的承载稳定性分析方法还较少，部分被相关行业所采用的计算理论也存在一些有待完善的地方。针对软弱夹层的破坏模式进行研究，采用极限分析上限法对软弱夹层的极限压力进行求解，提出的计算模式考虑了软弱夹层的宽厚比、层面摩擦条件、侧向偏移及附加力等因素的影响，结果可为合理分析软弱夹层的承载稳定性提供理论依据。

软弱夹层；极限荷载；破坏模式；上界法；层面摩擦条件

软弱夹层一般是指自然界中广泛存在的一种地质构造，其厚度相对较小，有时也称为软弱薄层。在地基处理工程中，如采用加筋换填部分软土层后也会形成类似的软弱夹层结构。目前围绕软弱夹层的研究是各类工程稳定性分析的一项重要内容，在边坡工程[1]、基坑工程[2]、隧道工程[3]等领域均有涉及，但目前多数研究侧重于软弱夹层的存在对拟建结构物的影响，没有对软弱夹层本身的破坏规律、承载机理作进一步分析。

存在软弱夹层的地基从结构上看属于层状地基。在现有的研究成果中，已有较多关于层状结构的应力场和变形场的弹性解答[4-5]，可用于层状地基的近似求解，但因忽略了土体的塑性，此类方法仍存在较大误差且不易于工程应用。从强度理论角度分析层状地基的极限荷载在一些文献中也有涉及，主要围绕上硬下软、上软下硬等情形并采用传统滑移线场分析方法确定其极限荷载[6]，但其中的剪切滑移线在软硬土层分界面上的分布规律带有较大不确定性，尤其是软弱夹层较薄时更为明显，给计算分析带来不便。实际上，软弱夹层的承载特性与其破坏模式密切相关，涉及到软弱夹层结构的尺度、材料强度等因素。下面结合软弱夹层的破坏模式对其极限荷载进行分析。

1　软弱夹层的破坏模式

考虑到软弱夹层的力学性质较上下土层明显低，极限状态下除了发生常规的剪切滑移破坏外，更容易产生沿夹层面发生挤出的破坏形式。我国《水利水电工程土工合成材料应用技术规范》(SL225-98)[7]、《土工合成材料应用技术规范》(GB50290-98)[8]、《化工建(构)筑物地基加筋垫层技术规程》(HG/T20708-2011)[9]均明确要求对加筋垫层下存在的软弱土层进行滑动挤出破坏模式的承载力验算，而并未采用传统地基承载力计算方法。Mandel等[10]对基底与下卧硬土层之间的软弱夹层也曾提出了塑性挤出的破坏模型。张道宽[11]对加筋软土路堤下软弱薄层的极限荷载进行差分法计算，认为夹层宽厚比超过时便可按塑性挤出的破坏模式进行承载力计算。虽然现有的研究成果提出了软弱夹层的塑性挤出破坏模式，且在一些行业规范中列出了具体的计算方法，但对该模式的发生条件却研究不充分，多数是定性判断。

实际上，基底软弱夹层的极限破坏状态与基底下夹层的厚度有很大关系，若基底软弱夹层厚度较大，则地基剪切滑动面的发展不受夹层面位置控制，可按均质地基方法进行分析；若基底软弱夹层厚度小，则不宜按传统地基破坏模式进行分析，而应该考虑夹层的塑性挤出破坏模式(图1)。

图1　不同厚度软弱夹层的破坏模式Fig.1　Failure mode of soft interlayer with various thicknesses

为了明确划分两类破坏模式，参照Terzaghi地基剪切破坏滑动面(基底完全粗糙)(图2)，对数螺旋曲线OC方程可写为[6]

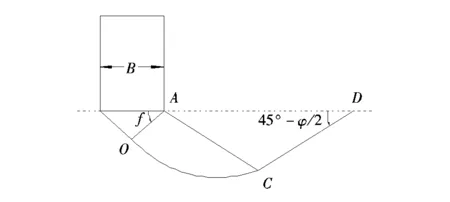
图2　Terzaghi破坏模式Fig.2　Failure mode of Terzaghi

(1)

式中：θ为螺旋曲线上任一矢径r与起始矢径的夹角，φ为内摩擦角。

对数螺旋线上任一点至地表距离为：

(2)

(3)

因此，软弱夹层的厚度H≤Hf时可考虑塑性挤出的破坏模式；H>Hf时可按常规均质地基破坏模式分析。

2　软弱夹层的挤压模型

当软弱夹层的厚度小于滑动面的临界距离，采用塑性挤出破坏模式进行极限荷载分析较符合其变形机制。考虑到夹层上下土层力学性质相对好于软弱夹层(如加筋垫层下存在的部分软弱薄层问题)，可以将软弱夹层上下岩土层当做准刚性层，形成一种夹层挤压结构进行分析。在夹层结构的理论解答上，早在1923年Prandtl[12]就对两块粗糙刚性平板挤压塑性材料进行了求解，所得的解答在金属材料加工领域被广泛应用并完善。张国霞结合Prandtl解答，对筏板基础下软弱夹层的极限荷载结合一般承载力算法进行了改进，提出了薄层挤压理论并被相关的行业规范直接引用[9,13]。考虑到Prandtl解在边界条件上的一些缺陷，Hill[14]改变了夹层面的粗糙条件，对其解答进行了完善，得到了夹层面压力随层面剪应力条件变化的解答。文献[15]也对Prandtl解在对称轴上应力条件的不足进行了修订。

上述成果在分析夹层面粗糙条件上虽有所改进，但对夹层材料仍采用均一的夹层面剪应力条件进行求解，所得解答不能反映夹层面粗糙条件及材料强度对层面不同位置摩擦条件的影响。同时，在分析过程中上述成果并未考虑软弱夹层侧向挤出时侧面变形导致的速度场改变，而是按照无侧鼓的刚塑性材料假定进行的分析。除了基于Prandtl解的相关理论外，对于塑性材料的挤压问题，翁克索夫通过大量实验验证认为，夹层塑性材料的挤压力与几何尺度、夹层面粗糙条件密切相关，并且夹层面的滑动是由粘滞区、制动区、滑动区构成，每一部分应该采用不同的摩擦条件[16](图3)。

图3　夹层面不同位置滑移规律Fig.3　Slide rule of different positions on layer surface

3　软弱夹层极限荷载分析

下面针对平面应变问题，根据翁克索夫不同夹层面摩擦条件的理论，采用极限分析上限法，考虑夹层侧向挤出破坏模式，对软弱夹层塑性极限荷载进行求解。

3.1挤压速度场确定

根据图4所示软弱夹层平面应变模型，宽度为b的刚性压板以速度v0沿-y方向挤压夹层材料。软弱夹层初始高度为h，材料以vx速度向两侧流动，侧面鼓形两端挤出偏移量l，两侧作用外力σ0。假设整个速度场连续，材料挤压过程中没有速度间断面，参照没有侧向鼓出效应时的速度场解答[17]，假定x向速度分量vx在y方向上呈指数曲线规律变化，可设vx为：

图4　软弱夹层挤压模型Fig.4　Squeezing model of soft interlayer

(4)

(5)

(6)

对上式积分可得：

(7)

根据边界条件vy|y=0=0，可得：

(8)

将上式代入(7)式后，再根据vy|y=h=-v0可得：

(9)

将(8)式、(9)式代入(7)式，(9)式代入(4)式，整理后得到以一个待定参数l表示的运动许可速度场如下：

(10)

3.2内部塑性变形功率

由上述速度场求得对应的应变率为：

(11)

(12)

由上限法原理计算材料挤压过程中的变形功率，经整理后得到：

(13)

上式取l=0时即可得到不考虑侧向鼓出效应的解答，结果与文献[17]一致。

3.3层面摩擦功率

夹层材料在变形过程中除了考虑内部的变形功率外，挤出过程中层面的摩擦效应也是消耗外部挤压功率的重要部分。本文分析中采用翁克索夫如图4所示的层面摩擦规律，其中3个不同的层面剪应力条件如下：

粘滞区OC段(0≤x≤xc=h)

(14)

(15)

(16)

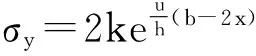
层面相对滑移速度为：

(17)

分别在上下层面考虑(14)～(16)式不同的摩擦条件，计算层面摩擦功率并累加可得：

(18)

3.4总变形消耗功率

假定夹层两侧作用的附加外力σ0沿夹层高度均匀分布，侧向挤出速度取(x=b/2，y=h/2)处的vx值，且无速度不连续的剪切功率，则附加外力速度场：

(19)

附加外力功率为：

(20)

若夹层达到极限状态所需平均挤压力为q，则夹层上真实挤压力功率可表示为：

(21)

综上，结合材料内部变形功率、层面摩擦功率、附加外力功率之和与挤压功率相等的条件，可得到极限挤压力的上限解：

(22)

上式中不考虑侧面鼓形挤出影响时可取l=0；不考虑侧向附加外力影响时可取σ0=0。

式(22)较之于现有其他软弱夹层挤压理论除了考虑侧向附加外力影响外，更主要的是考虑层面多种摩擦条件;在计算过程中将夹层面的摩擦条件在h、处分段进行考虑，这种方式对于建立轴对称平面问题或空间问题模型更符合应力边界条件。

4　计算结果分析与讨论

为了分析所得到的挤压力解答(22)式，不妨取宽度b=2m～10m，厚度h=1m的软弱夹层为计算对象，不考虑侧向附加力及材料自重影响。软弱夹层取饱和不排水强度，按(3)式的破坏模式判别式可知，上述夹层尺度可按塑性挤出破坏模式进行分析。

此外，由式(15)中xb=b/2+h(ln2u)/2u可知，夹层面摩擦系数u大于0.5时，xb≥b/2,即此时夹层材料不会沿层面产生滑动，材料完全粘附在层面上，塑性挤出是由自身强度剪切破坏导致的滑移。计算结果也表明u≥0.5时，各宽厚比下的极限压力几乎不变。因此，为反映不同夹层面摩擦系数对挤压力的影响，本次分析过程中取u=0.1～0.5。

按文中方法，以下给出夹层侧向偏移量l/b=0%～10%时极限挤压力变化的结果。另外，为了与已有的相关理论进行对比，对于上述夹层参数，除了给出本文方法的计算结果外，还列出了板面摩擦条件分别按τ=mk(m为粗糙度系数，m=0表示完全光滑，m=1表示完全粗糙)、τ=u′σz[14](u′含义同u，σz为板面坚向压力)计算的极限压力结果(其中极限压力以Q/k表示(Q=qb))。

4.1侧向偏移量对极限荷载的影响

图5所示为u=0.3时不同夹层侧向偏移量下极限压力随宽厚比的变化关系。在一定的夹层材料强度下，随着宽厚比的增加无论是否考虑侧向挤出偏移，极限荷载均随宽厚比增加而增大，反映了软弱夹层的几何尺度对极限荷载的影响。因为夹层面存在摩擦阻力，侧向偏移量对极限荷载的影响随着夹层宽厚比的增加而逐渐显著。在宽厚比较低时，几种侧向偏移量下的极限荷载几乎相等;但当夹层宽厚比增加至10时，考虑和不考虑侧向偏移量的极限荷载相差近1倍。实际上挤压理论中考虑侧向偏移量正是反映了夹层面粗糙条件对侧向挤压流动的限制。不考虑侧向偏移量时，夹层的侧向挤出在两侧上下层面处均匀流动，材料强度发生较快损失造成极限压力偏低。

图5　不同侧向偏移量时极限压力(u=0.3)Fig.5　Ultimate pressure with different lateral offset(u=0.3)

因此，实际工程中对于宽厚比较大的软弱夹层，在采用塑性挤出破坏模式及挤压理论对其进行承载稳定分析时,不宜忽视侧向挤压偏移量的影响。

4.2层面摩擦条件对极限荷载影响

图6反映了b=10 m，l/b=0%～10%尺度下不同层面摩擦系数对极限荷载的影响。通过计算结果不难发现，无论是否考虑侧向偏移量，极限压力均随摩擦系数增加而增大，直至摩擦系数达到0.5时极限压力变化趋缓，不再随摩擦系数增大而提高。不考虑侧向偏移量时极限压力随摩擦系数的变化趋势与考虑侧向偏移量时极限压力随摩擦系数的变化趋势基本一致，但在层面摩擦系数较大时极限压力受侧向偏移量的影响略高于低摩擦系数情况。

图6　摩擦系数对极限压力的影响(b=10 m)Fig.6　Effect of friction coefficient on ultimate pressure

图7　本文解答与摩擦条件τ=mk的对比Fig.7　Solution comparison between this text and that with friction condition of τ=mk

图8　本文解答与摩擦条件τ=uσz的对比Fig.8　Solution comparison between this text and that with friction condition of τ=uσz

图7、图8分别给出了不考虑侧向偏移量影响下的解答(下称“本文方法”)、夹层面采用单一τ=mk条件以及τ=u′σz下的解答结果。由图中的结果可知，本文方法在较低夹层宽厚比时与其他方法差别不大;但随着宽厚比增加，其他方法的极限压力随摩擦系数(m，u′)的增加等比例增大，相当 于无限制地放大了层面摩擦系数对夹层挤压力的影响。本文方法在层面摩擦系数达到0.5时极限压力不再随摩擦系数增加而增大，考虑到一定尺度的夹层材料极限挤压力由强度和摩擦条件两方面控制，本文的解答较为符合实际。此外，在夹层面极端粗糙的情况下，几种方法在各宽厚比情况下解得的极限压力相差不大，本文结果处于另两种方法之间。

因此，对于软弱夹层层面粗糙程度对极限压力的影响问题，本文计算式能反映出软弱夹层的极限压力并非完全随摩擦系数的增加而增大;摩擦系数增大至一定程度时的夹层挤出破坏可以考虑为材料自身强度破坏。

5　结论

围绕软弱夹层挤出破坏，考虑层面不同摩擦条件及夹层侧向偏移等因素，导出了软弱夹层的极限压力计算式并对计算结果进行了分析比较。

1)分析了发生挤压破坏的软弱夹层临界厚度Hf。当软弱夹层厚度小于此临界厚度时宜采用挤压破坏模式分析其极限压力。

2)软弱夹层的极限压力随夹层宽厚比增加而增大；对于宽厚比较大的软弱夹层，建立挤压模型时是否考虑夹层侧向偏移对极限压力影响很大；同时，软弱夹层的极限压力随夹层面粗糙程度提高而增大，但当摩擦系数增加至一定值后，其对软弱夹层的极限压力影响可忽略。

3)较之于传统挤压理论，提出的软弱夹层极限压力计算式，能较全面反映夹层强度、层面摩擦条件、侧向偏移、两侧附加外力等因素的影响，在实际工程中对软弱夹层的承载稳定性分析具有一定的借鉴意义。

[1] 李忠，杨俊.基于MPGA的复杂应力状态边坡稳定性分析[J].岩土力学,2015,36(5):1 488-1 495.

[2] 单仁亮，董洪国，陈代昆.中深部含软弱夹层的深基坑土钉支护失稳破坏数值模拟分析[J].岩土工程学报,2014,36(S2):30-35.

[3] 吴旭平，杨新安，李亚翠，等.含软弱夹层浅埋隧道变形特性及控制指标研究[J].岩石力学与工程学报,2014,33(S1):2 685-2 691.

[4] 艾智勇，苏辉，成怡冲.求解层状地基平面应变问题的解析层元法[J].岩土工程学报,2011,33(11):1 797-1 800.

[5] 钟阳，张永山.求解多层弹性半空间轴对称问题的精确刚度矩阵法[J].力学季刊,2003,24(3):395-400.

[6] 钱家欢，殷宗泽.土工原理与计算[M].北京：中国水利水电出版社,1996.

[7] 住房与城乡建设部.中华人民共和国水利部.SL/T225-98水利水电工程土工合成材料应用技术规范[S].北京：中国水利水电出版社，1998.

[8] 住房与城乡建设部.中华人民共和国水利部.GB/T50290-2014土工合成材料应用技术规范[S].北京：中国计划出版社，2015.

[9] 山西华晋岩土工程勘察有限公司.HG/T20708-2011化工建(构)筑物地基加筋垫层技术规程[S].北京：中国计划出版社，2011.

[10]MandelJ，SalerconJ.Forceportanted'unsolsuruneassiserigide(étudethéorique)[J].Géotechnique. 1972:79-93.

[11] 张道宽. 土工织物加强软土路基的研究[D].北京：铁道部科研院,1987.

[12]PrandtlL.AnwendungsbeispielezueinemHenchyschenSatzüberdasplastischeGleichgewicht[J].ZeitschriftförangewandteMathematikundMechanik. 1923, 3(6):401-406.

[13] 张国霞. 基础工程学[M].北京：中国建筑工业出版社,1991.

[14]HillR.Themathematicaltheoryofplasticity[M].Oxford:Oxforduniversitypress,1950.

[15] 殷勇，周国庆.软弱夹层的极限荷载分析[J].岩土力学,2015,36(4):1 035-1 040.

[16] 翁克索夫E.п.塑性的工程理论[M].北京：科学出版社,1963.

[17] 李立新，胡盛德. 塑性力学基础[M].北京：冶金工业出版社,2009.

(责任编辑：张英健)

ResearchontheUltimateLoadofSoftInterlayerConsideringtheEffectofLateralExtrusion

YINYong1,2

1． State Key Laboratory of Geomechanics and Deep Underground Engineering，China University of Mining & Technology，Xuzhou Jiangsu 221008，China;2． School of Civil Engineering，Yancheng Institute of Technology，Yancheng Jiangsu 224051，China

Softinterlayerstructureiswidelyencounteredduringconstructionofengineeringincoastalareas.Foritsweakproperties,itusuallybringshazardstothesubsequentstabilityofprojects.Atpresent,theanalysismethodofbearingcapacityofsoftinterlayerarestillfew,andtherearealsosomedeficiencyofcalculationtheoryneedtobeimprovedwhichhavebeenadoptedbytherelevantindustry.Thefailuremodeofsoftinterlayerisresearchedinthistext，theultimatepressureofsoftinterlayerissolvedbytheupperboundmethodinthelimitanalysisaswell.Theinfluenceofthethicknessratio,thefrictioncondition,thelateraloffsetandtheadditionalforcetothesoftinterlayerareconsideredinthecalculationmethod.Theoutcomecanprovideatheoreticalbasisforthereasonableanalysisofthebearingstabilityofthesoftinterlayer.

Softinterlayer;Ultimateload;Failuremode;Upperboundmethod;Frictionconditiononstratificationplane

10.16018/j.cnki.cn32-1650/n.201503002

2015-05-22

国家重点基础研究发展计划(973) 资助项目(2012CB026103)

殷勇(1980-)，男，江苏建湖人，讲师，博士生，主要研究方向为软土力学性质与工程。

TU443

A

1671-5322(2015)03-0007-06