多走一步，感受别样数学风景

苏志强

一、纵横延伸，从一般走向特殊

归纳推理是形成创造能力的根本。在保证学生获得基础知识，形成基本技能的前提下，教师应当引导学生对知识横向拓宽、纵向掘深，让学生亲历发现问题、提出问题、分析问题和解决问题的过程，促使学生的认知从一般走向特殊。

例如，教学“3的倍数的特征”时，教师让学生在找3的倍数（3、6、9、12、15、18、21……）的基础上，相加这些倍数各位上的数的和，得出3的倍数的特征。再出示巩固练习：下面各数中，哪些数是3的倍数？（3、6、23、45、18、93、86、120、237、126、69、332、891、89、56913、3465689、222222222、11111111111111）

判断一个数是不是3的倍数，是最基本的要求，用一般方法就能解决。教学至此，教师还要引导学生多“走”一步——仔细观察这些数，从中可以发现哪些更为有趣的数学规律？让学生的思维从“现有发展区”走向“最近发展区”。

（1）个位是3、6、9的数，有的是3的倍数，有的不是3的倍数。像23、86、89的个位分别是3、6、9，但它们都不是3的倍数。所以判断一个数是不是3的倍数，不能像判断2、5的倍数那样，只看个位上的数。

（2）3的倍数，不一定是6的倍数；6的倍数一定是3的倍数。像45是3的倍数，但它不是6的倍数；6本身就是3的倍数，所以6的倍数一定是3的倍数。

（3）9的倍数不一定是6的倍数，但一定是3的倍数。像45是9的倍数，但不是6的倍数；9本身就是3的倍数，所以9的倍数一定是3的倍数。

（4）3的倍数可以是奇数，也可以是偶数。像93、120都是3的倍数，93是奇数，120是偶数。

……

上述结论，有旧知识与新知识的融合，有简单方法与复杂方法的交错。学生间相互补充、相互纠正，逐一举例、验证、概括、推理，源于学生的脑，出自学生的口，才是学生智能的挖掘，心灵的激荡，迸发着智慧的火花，积淀着创造的能量。

二、科学验证，从动作走向心智

部分学生思维水平有限，逻辑能力不强，知识储备不够，在操作实践活动中，对所看到的结果、所获得的结论，往往停留在已有知识经验或直观思维上，未能多“走”一步，从数学的角度对操作结果做深层次的科学验证，从而获得真正意义上的数学，促进心智的提升与技能的形成。

例如，教师让学生用一张长10厘米，宽8厘米的长方形纸片折最大的正方形。学生凭借自己的生活经验和知识储备，很快地折出了一个正方形。按照常规的做法，教师就是比一比、评一评谁折得好，谁折得漂亮。师生的思维都停留在简单的、已有的正方形经验的判断上。此时，教师要是能以怀疑的眼光，质疑学生：“所折的四边形真的是正方形吗？”则会给学生的喜悦带来思维的冲击。“为什么是正方形？”这一问题把课堂推向辩论的高潮。

生：可以用三角板量出所折图形的边长，四条边的长度如果都是8厘米就是正方形。

生：还要量四个角的度数，四个角都要是直角。只有四个角是直角，四条边都相等，才能确定所折的图形是正方形。

生：这种方法不够严谨，要是度量的时候有误差，就不能百分之百确定它是正方形。我们可以观察所折的四边形，从中找到它是正方形的证据。

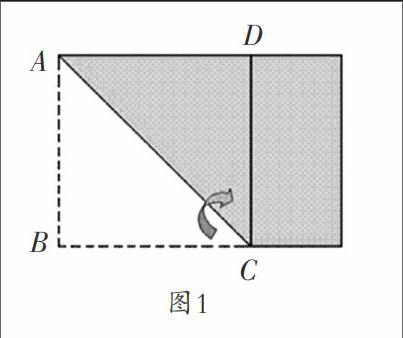
教师顺势在黑板上画了一个图示（图1），标上字母，以便学生发言。

生：由原长方形纸片可知，∠B和∠BAD都是直角，沿AC边对折后，∠B与∠ADC完全重合，说明∠ADC也是直角；同样可得∠BCD也是直角。由此确定四边形ABCD四个都是直角。

生：沿AC边对折后，AB与AD完全重合，说明AB=AD=8厘米；同样可得DC=BC=8厘米。由此确定四边形ABCD四条边相等，都是8厘米。

生：四个角是直角，四条边都相等的四边形一定是正方形，所以所折的四边形一定是正方形。

三、模型支撑，从抽象走向具体

数学，具有很强的抽象性。对于以具体形象思维为主的小学生来说，要引导他们通过观察、分析、概括、归纳等活动，从简单到复杂，从具体到抽象，解开数学奥秘，探究数学规律，解决数学问题。教师还要跳出教材，引导学生在抽象的知识上寻找思维的“支撑点”，探求“支撑物”，使他们学有所“依”，把抽象的思维建立在具体的事物上。

例如，教学“乘法运算定律”时，有位教师引导学生根据主题图提供的信息和教材中的三个数学问题分别探究了乘法交换律、乘法结合律和乘法分配律的意义，然后出示一些成组的习题引导学生抽象概括出三个定律的字母公式。这样的学习看似深刻，实则肤浅。学生对定律意义的理解、字母公式的概括并不清晰。为此，教师要以此为基础，引导学生打开思维的另一条通道——“能不能借助长方形的面积计算来探究乘法运算定律呢？”一石激起千层浪，学生或画、或算，找到了全新的学习历程。

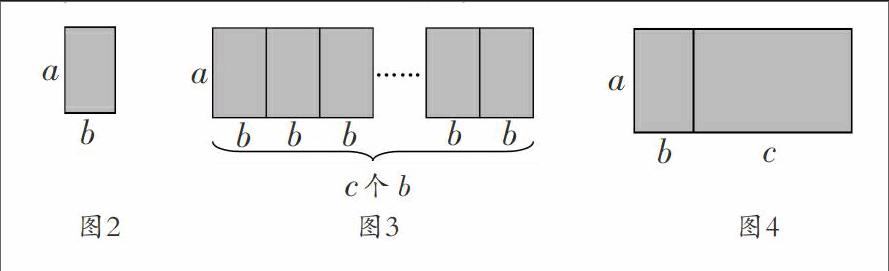
图2，长方形的面积可以用a×b表示，也可以用b×a表示，不管哪种表示方式，都是同一个图形的面积，也就是说它们的面积相等，即a×b=b×a，这个关系式反映的就是乘法交换律的特征。

计算图3长方形的面积有两种方法。一是先算一个小长方形的面积a×b，再算c个长方形的面积a×b×c；二是先算长方形的长b×c，再算长方形的面积a×（b×c）。两种方法所计算的长方形面积相等，即a×b×c=a×（b×c），这个关系式反映的就是乘法结合律的特征。

图4反映的是乘法分配律的特征。计算长方形的面积，可以直接计算长b+c，宽a的长方形的面积，即a×（b+c）；也可以用左长方形的面积a×b加右长方形的面积a×c，即a×b+a×c。两种计算方法面积相同，所以a×（b+c）= a×b+a×c。

学生从“数”到“形”，对乘法运算定律积累了更为丰富的表象，心灵深处有了更为深刻的体验、感受，枯燥的文字表述、抽象的字母公式有了图形的支撑，变得有“模”有“型”，具体实在，丰富有趣。多“走”一步，看得见、摸得着、想得到，既可建立清晰的数学模型，又能展现数形结合的神奇魅力。

（作者单位：福建省德化县尚思小学 责任编辑：王彬）endprint