计及温度条件下的微穿孔板结构优化设计

刘淑梅，孔德义，李山山，李子博，赵湛



计及温度条件下的微穿孔板结构优化设计

刘淑梅1,2，孔德义2，李山山1,2，李子博1,2，赵湛3

(1. 中国科学技术大学自动化系，安徽合肥230026；2. 中国科学院合肥智能机械研究所，安徽合肥230031；3. 中国科学院电子学研究所传感技术国家重点实验室，北京100190)

微穿孔板吸声体是由穿孔直径在1 mm以下的薄板和板后空腔组成的共振吸声结构，其结构通常可利用经典的微穿孔板理论来设计。但在温度变化条件下，经典的微穿孔板理论已经不足以设计出满足要求的微穿孔板结构。文中在设计微穿孔板吸声结构时，不仅考虑了结构参数孔径、板厚、孔间距及空腔深度对微穿孔板吸声特性的影响，又计入了温度这一参数。拟采用改进的粒子群优化算法，分别对一定温度下的单层和双层微穿孔板吸声体的结构参数进行优化设计，搜索得到最优的参数组合，使其在给定的频带范围内平均吸声系数最高。优化结果表明：利用改进的粒子群算法设计出的微穿孔板吸声结构在给定频率范围内吸声系数较大，且符合给定温度的要求。

微穿孔板；粒子群优化算法；优化设计；吸声系数

0 引言

微穿孔板吸声体是由我国著名声学专家马大猷教授于1975年首次提出的[1]，自提出以来，就以其结构简单、环保、抗腐蚀等诸多优点被广泛应用于各种常温条件下的噪声控制问题中。孙富贵[2]等人理论预测并通过高温驻波管实验验证了纤维材料在高温下的吸声特性，发现其吸声性能均随着温度的升高而减小。西北工业大学的王鹏[3]等人针对微穿孔板在高温燃烧室的应用，采用理论分析和仿真的方法，分析了高温条件下微穿孔板的声学特性。但文献[3]中并没有对低温下微穿孔板结构的吸声特性进行讨论，由于本项目组主要研究飞机的机翼与电机降噪，而飞机在高空飞行时，空气温度均低于270 K。本文在分析了微穿孔板在高温和低温条件下的吸声特性后，发现传统的微穿孔板的结构参数设计理论变得不再适用。因此，急需提出一个计及温度条件下的微穿孔板结构优化设计方法，以满足其在偏离常温条件下的应用。

近年来，随着智能优化算法的兴起，文献[4]采用标准遗传算法(Genetic Algorithms, GA)来解决双层微穿孔板吸声体结构参数的优化问题。然而，标准遗传算法易早熟，容易陷入局部最优值。除此之外，Heidi Ruiz[5]等人基于模拟退火算法实现了对多层微穿孔板吸声结构的优化设计。然而，虽然模拟退火算法计算过程简单，鲁棒性强，可用于求解复杂的非线性优化问题，但其存在收敛速度慢、执行时间长等缺点。粒子群优化(Particle Swarm Optimization, PSO)算法最早由Kennedy和Eberhart[6]在1995年提出的，通过模拟鸟群行为来解决优化问题，该算法具有收敛速度快、操作简单等特点。鉴于此，王静云[7]等人应用标准的粒子群优化算法设计了锥形孔微穿孔板结构，结果表明，利用粒子群算法可快速有效地找到满足设计需要的结构，方便又快捷，但标准的粒子群优化算法易产生早熟收敛，局部寻优能力较差，而且文献[7]中仅对微穿孔板吸声结构里的单个参数以及双参数进行了优化。

本文依据微穿孔板吸声结构的基本理论，考虑了高温以及低温对微穿孔板吸声特性的影响，利用比标准粒子群优化算法以及标准遗传算法搜索能力更强、收敛速度更快的改进的粒子群优化算法，分别对单层和双层微穿孔板吸声体的全部结构参数进行优化设计，搜寻最优参数组合，使其在选定频率范围内平均吸声系数最高，从而达到高吸收的降噪效果，而且设计出的微穿孔板吸声结构，可以分别满足高温以及低温环境下的降噪要求。

1 微穿孔板吸声结构的基本方程

1.1 单层微穿孔板吸声结构的数学模型

根据经典的微穿孔板理论，单层微穿孔板基本结构示意图及其等效电路图如图1所示[1]。

正入射时的吸声系数为[8]

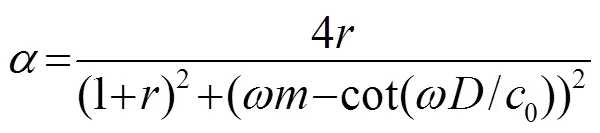
式(1)中：

(2)

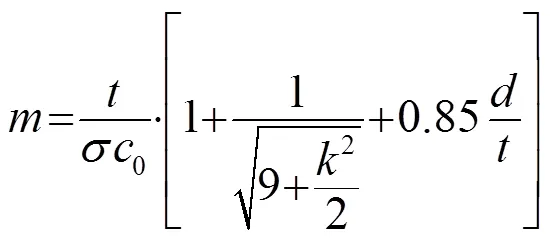
(4)

其中：为孔径，为板厚，为空腔深度，为孔间距，为穿孔率，为穿孔常数，为常温下声速，为运动粘滞系数。

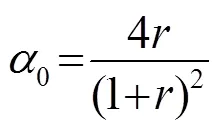
1.2 双层微穿孔板吸声结构的数学模型

双层串联微穿孔板吸声体的结构及其等效电路如图2所示[1]。

当平面声波垂直入射时，双层串联微穿孔板吸声体的法向吸声系数可表示为[4]

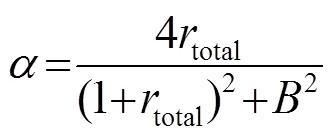
(8)

以上均为微穿孔板吸声体在常温下的数学模型，下文将给出计及温度变化条件下的微穿孔板吸声体的声阻抗以及吸声系数的计算公式。

2 温度对微穿孔板吸声体数学模型的影响

在影响微穿孔板的参数中，随着温度的不同，气体的粘性、密度以及声音在空气中传播的速度均有所改变[9]。

从物理学知道，任何状态下的气体，压强、密度和温度三者之间存在如下关系：

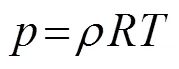
且有

(11)

其中，称为气体常数，常温下等于286.85，288.15 K。

在许多空气动力学的问题里，粘性力和惯性力同时存在，即[9]：

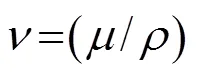
根据热力学方程可得

综合以上参数，单层微穿孔板吸声体相对声阻为

其中

(16)

(18)

图3为不同温度下任取的一组单层微穿孔板吸声特性的计算结果，其结构参数分别为：=0.15 mm，=0.8 mm，=0.248 mm，=20 mm，图3给出了其在不同温度下的垂直入射吸声特性曲线，从该图中可以看出在大于300 K或低于270 K时，微穿孔板最大吸声系数从接近于1.0下降到0.6以下，特别是在=800 K时，最大吸声系数已经减小至0.2以下，其有效吸声带宽随着温度升高减小较明显，且共振峰随着温度升高均向高频偏移。可见利用传统的微穿孔板理论来设计微穿孔板结构参数不再能满足非常温下环境的降噪要求，因此本文将采用改进的粒子群优化算法，在计及温度的条件下对微穿孔板吸声体的结构参数进行优化设计。

3 粒子群优化算法

3.1 基本粒子群算法

PSO算法的基本思想是随机初始化一群没有体积和质量的粒子，每个粒子都为优化问题的一个解，并由目标函数为之确定一个适应值。

设在一个维的搜索空间中，由个粒子组成的种群={,…,…}。其中第个粒子的位置为=(,,…,)，其速度为=(,,…,)，它经历过的最好位置记为=(,,…,)，也称为。群体所有粒子经历过的最好位置的索引号用符号表示，即，也称为。对于每一代，它的第维的速度和位置根据如下方程进行变化：

(21)

其中：=1, 2, …,，为维数，=1, 2, …,，为种群规模，为惯性权重，和为学习因子，对PSO的收敛速度影响颇大。通常取== 2或。和是在[0,1]区间的随机数。

3.2 改进的粒子群优化算法

PSO算法的搜索性能取决于对全局搜索和局部搜索能力的平衡，这很大程度依赖于算法的控制参数，包括种群规模、迭代次数、惯性权重、学习因子等。本文通过对的改进来优化微穿孔板结构参数。

4 改进的粒子群算法对计及温度条件下的微穿孔板结构参数优化

在计及温度条件下，单层微穿孔板优化参数分别为板厚，孔径，孔间距以及空腔深度，一般的算法不能够最大限度地进行全局搜索，从而得不到较好的优化效果。基本粒子群算法由于其易于实现、设置参数少、收敛速度快等优点，得到广泛应用。但基本的粒子群算法也容易陷入局部最优，本文将利用改进的粒子群算法来解决单层与双层微穿孔板吸声结构的参数优化问题。

4.1 适应度函数设计

采用在白噪声条件并计及温度条件下以微穿孔板计算频率范围内吸声系数曲线最饱满为目标构建适应度函数：

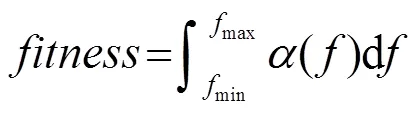
(24)

4.2 确定决策变量和约束条件

设定温度分别为500 K和200 K，优化频率范围为100~4000 Hz，设定一固定频率=1300 Hz。以单层微穿孔板吸声体的结构参数(孔径，板厚，孔间距，空腔深度)为决策变量，单位均为mm。将约束条件设为：2<≤100，0.2≤≤2，0.5≤b≤4，0.1≤≤2.0。

双层微穿孔板吸声结构的优化模型与单层类似，由于双层微穿孔板吸声频带范围较宽，此时将不考虑单个板的共振频率，仅在100~4000 Hz频率范围内寻优。双层微穿孔板优化参数变为8个，为了加工方便可取，2<+≤100，0.1≤≤2，0.1≤≤4，0.1≤≤4，0.04≤≤2.0，0.04≤≤2.0，取温度=500 K进行优化。

4.3 改进的PSO算法的寻优过程

粒子群优化算法寻优的一般步骤：

Step 2：适应度函数评价。选取式(24)作为适应度函数。

Step3：控制参数的更新。令迭代步数增加，完成惯性权重的更新。

Step 4：粒子速度和位置更新。

Step 5：个体最佳位置更新。

Step 6：全局最佳位置更新。

4.4 单层微穿孔板优化结果

当=500 K时，单层微穿孔板优化结果如表1所示。当=200 K时，单层微穿孔板优化结果如表2所示。

表1 T=500 K时，单层微穿孔板优化结果(单位：mm)

表2 T=200 K时，单层微穿孔板优化结果(单位：mm)

表1与表2为本文优化的单层微穿孔板吸声体结构参数以及常温下未计及温度条件的一组优化参数。图4对比了本文考虑温度条件的优化结果与未考虑温度条件的优化结果分别在两种温度下的吸声特性。从图4可见，未计及温度条件优化的单层微穿孔板结构参数在高温以及低温环境下，其最大吸声系数均不到0.6，而其在常温下最大吸声系数几乎为1.0(见图3中=300 K时的频率特性曲线)。本文在考虑了温度对微穿孔板吸声结构的降噪性能的影响后，设定一固定频率=1300 Hz，采用改进的粒子群优化算法对其结构参数进行优化，优化结果如图4所示，在两种温度下，运算结果均能满足最大吸声系数、共振频率以及温度的设计要求。

4.5 双层微穿孔板优化结果

当=500 K时，双层微穿孔板优化结果如表3所示。

表3=500 K时，双层微穿孔板优化结果(单位：mm)

Table 1 Optimization results of double layer MPPs at T=500 K (unit: mm)

将表3中两组结果参数代入=500 K下的双层微穿孔板的吸声系数公式，可求得吸声系数对比曲线如图5所示。

表3中，文献[4]优化结果为在常温下计算得到的，优化后的双层微穿孔板结构参数在常温下吸声性能较好，如图6所示。图5对比了文献[4]与本文设计的微穿孔板结构在=500 K时的垂直入射吸声特性曲线。可以发现文献[4]设计的微穿孔板结构已经不能满足=500 K时的降噪要求。而本文在计及温度对微穿孔板吸声性能的影响后，设计出的双层微穿孔板的结构参数，在设计的频率范围内吸声系数均较高，有效吸声频带较宽。

5 结论

本文根据前人对计及温度条件下的微穿孔板吸声特性的研究，发现温度变化对微穿孔板的相对声阻、相对声质量、最大吸声系数以及共振频率均有很大影响。在非常温下，利用传统的微穿孔板结构设计理论已经不足以设计出满足环境要求的微穿孔板吸声结构。本文利用操作简单、收敛速度快的改进的粒子群优化算法，分别对单层和双层微穿孔板吸声体的结构参数进行优化设计。结果表明，在高温及低温条件下，利用改进的粒子群算法设计出的微穿孔板吸声结构，均可以满足该温度下的降噪要求。

考虑到本文仅提出了一种理论分析方法，实验验证是有必要的。但由于硕士论文阶段工作时间和现有实验条件的原因，难以开展。下一步工作中拟采用有限元分析的方法进行仿真验证，考虑温度场对声-热转换的影响，与本文结果进行对比。

[1] 马大猷. 微穿孔板吸声结构的理论和设计[J]. 中国科学, 1975, 18(1): 38-50.

MAA Dayou. Theory and design of microperforated panel sound-absorbing constructions[J]. Scientia Sinica, 1975, 18(1): 38-50.

[2] SUN Fugui, CHEN Hualing, WU Jiuhui, et al. Sound absorbing characteristics of fibrous metal materials at high temperatures[J]. Applied Acoustics, 2010, 71(3): 221-235.

[3] 王鹏, 王敏庆, 樊晓波. 温度变化条件下微穿孔板声学特性研究[J]. 振动、测试与诊断, 2007, 27(4): 267-269.

WANG Peng, WANG Minqing, FAN Xiaobo. Acoustic characteristic of microperforated panel in altering temperature[J]. Journal of Vibration Measurement and Diagnosis, 2007, 27(4): 267-269.

[4] 隋林强, 赵晓丹, 祝瑞银. 遗传算法在双层微穿孔板结构优化设计中的应用[J]. 噪声与振动控制, 2006, 26(2): 49-52.

SUI Linqiang, ZHAO Xiaodan, ZHEN Ruiyin. Multilayer microperforated structure optimization design using genetic algorithm[J]. Noise and Vibration Control,2006, 26(2): 49-52.

[5] Heidi Ruiz, Pedro Cobo, Finn Jacobsen. Optimization of multiple-layer microperforated panels by simulated annealing[J]. Applied Acoustics, 2011, 72(10): 772-776.

[6] Russell Eberhart, James Kennedy. A New Optimizer Using Particle Swarm Theory[C]// Proceedings of the Sixth International Symposium on Micro Machine and Human Science. Nagoya, 1995: 39-43.

[7] 王静云, 常安定, 徐春龙, 等. 应用粒子群优化算法设计锥形孔微穿孔板结构[J]. 陕西师范大学学报(自然科学版), 2014, 42(2): 37-41.

WANG Jingyun, CHANG Anding, XU Chunlong, et al. Application of particle swarm optimization algorithm designing tapered hole microperforated panel structure[J]. Journal of Shaanxi Normal University(Natural Science Edition), 2014, 42(2): 37-41.

[8] 马大猷. 微穿孔板吸声体的准确理论和设计[J]. 声学学报, 1997, (5): 385-393.

MAA Dayou Y. General theory and design of microperforated-panel absorbers[J]. Acta Acustica, 1997, 22(5): 385-393.

[9] 钱翼稷. 空气动力学[M]. 北京: 北京航空航天大学出版社, 2004.

QIAN Yiji. Aerodynamics[M]. Beijing: Beihang university press, 2004.

[10] 江善和, 江巨浪, 吴磊. 基于粒子群算法的一种非线性PID控制器[J]. 计算机技术与发展, 2007, 17(4): 71-74.

JIANG Shanhe JIANG Julang, WU Lei. A nonlinear PID controller based on particale swarm tuning algorithm[J]. computer technology and development, 2007, 17(4): 71-74.

The structure optimization of micro-perforated panel absorber considering the effect of temperature

LIU Shu-mei1,2, KONG De-yi2, LI Shan-shan1,2, LI Zi-bo1,2, ZHAO Zhan3

(1. University of Science and Technology of China, Hefei 230026,Anhui, China;2. Institute of Intelligent Machines, Chinese Academy of Sciences, Hefei 230031,Anhui, China;3. State Key Laboratory of Transducer Technology, Institute of Electronics, Chinese Academy of Science, Beijing 100190, China)

As a new promising sound absorption material, micro-perforated panel absorbers (MPPAs) have been successfully applied in various noise control occasions, even capable of working at harsh environments, including high temperature circumstances. According to Maa’s model, the sound absorption performance of a MPPA can be theoretically predicted as four parameters were chosen, i.e., the perforation diameter d, the panel thickness t, the distance between centers of adjacent perforations b, and the depth of the air gap D. However, the Maa’s model turns to be inaccurate at high temperatures. In this work, the temperature T is included into Maa’s model as the fifth parameter besides the four parameters. Simulation results show that better prediction accuracy could be obtained at high temperatures with the revised model. Furthermore, an improved particle swarm optimization algorithm is proposed to search for optimal structure parameters of mono-layer and double-layer MPPAs at given temperatures, which will facilitate the design work for MPPAs working at high temperatures.

micro-perforated panel; particle swarm optimization algorithm; optimization design; sound absorption

TB5

A

1000-3630(2015)-04-0347-06

10.16300/j.cnki.1000-3630.2015.04.011

2014-07-07;

2014-09-12

国家自然科学基金资助项目(11474291)。

刘淑梅(1989－), 女, 安徽亳州人, 硕士研究生, 研究方向为噪声与振动控制。

刘淑梅, E-mail: liu5652025@163.com