基于系统解卷积技术的波纹管压浆质量检测

成锦，韩庆邦,2，陈媛，范洪辉，殷澄，朱昌平



基于系统解卷积技术的波纹管压浆质量检测

成锦1，韩庆邦1,2，陈媛1，范洪辉3，殷澄1，朱昌平1

(1. 河海大学物联网学院，江苏常州 213022； 2. 河海大学淮安研究院，江苏淮安 223001； 3. 江苏理工学院计算机工程学院，江苏常州 213001)

提出了一种基于系统解卷积技术的波纹管压浆质量检测方法，利用系统分析技术结合解卷积补偿特性处理回波信号，并分析处理后的波形的首波响应时间，对缺陷的位置及大小做出判断。利用有限元进行了理论模拟仿真，采用系统解卷积技术处理并分析回波数据，结果表明解卷积后的波形的首波的响应时间与缺陷表面深度值存在一一对应关系。通过实际制作模型并进行实验测量，验证了仿真的结果。

系统；解卷积；无损检测；有限元；缺陷

0 引言

波纹管结构被广泛应用于孔道预应力混凝土结构中，波纹管压浆质量不合格将会导致严重的安全事故问题。目前，孔道压浆施工中经常出现的质量问题有压浆不密实、有空隙、孔道未被水泥浆完全充满存在缺陷、水泥浆体由于硬化收缩过大而与孔道分离出现缺陷等。孔道压浆质量将直接影响预应力构件的耐久性、承载能力和抗裂性能。在无损检测技术中，用脉冲回波法[1]可以检测出波纹管中钢筋的腐蚀程度[2]，并且对定位结构体中的裂纹、空腔和缺陷有一定效果[3]。但是混凝土结构系统由混凝土、波纹管和钢绞线等组成，介质较多，超声波在这种结构内传播会有衰减，接收到的回波信号强度较低，而且传播过程中还存在着由各个介质面引起的反射波、折射波与透射波[4]，故由缺陷引起的反射回波会淹没在这些波中，难以区分缺陷信息。基于(Stack Imaging of spectral amplitudes Based on Impact-Echo, SIBIE)的无损检测法可以识别缺陷位置[5]，利用信息熵方法也可以定性地识别缺陷的横向尺寸[6]，但是对于那些横向尺寸不大、但纵向尺寸较大的缺陷，这些方法的分辨率就大大降低，难以分辨纵向危害性的缺陷，导致漏判、误判。本文从系统角度出发，结合解卷积方法处理回波信号，旨在提取缺陷纵向敏感信息，并通过仿真及实验进行了验证。

1 理论基础

1.1 缺陷响应的解卷积模型

解卷积运算[7,8]是已知输出求取输入信号的一种方式，也可以看成信道的一种补偿特性。如图1所示，是缺陷距离检测面的深度，是缺陷距离大平底面的深度。区域1系统为无缺陷系统ref。脉冲电信号加载在发射换能器上，经过电-声转换过程发射平面纵波，超声传播到深度处(过程)，再继续传播到大平底面并且经过大平底反射后，反向传播到深度处(过程)，继续反向传播被接收换能器接收(过程)，经声-电转换过程，成为接收电信号。

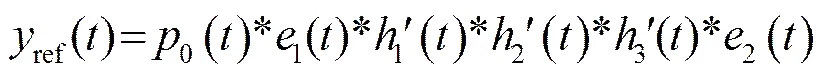
式中，“*”代表卷积运算。

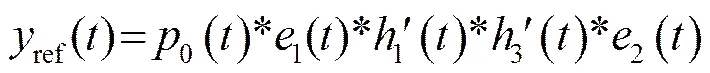
图1所示的区域2系统为含有某个缺陷的系统。脉冲电信号加载在发射换能器上，经过电-声转换过程发射平面纵波，超声传播到缺陷表面处(过程)，被缺陷散射(过程)，然后一部分继续传播到大平底面并且经过大平底反射后，反向传播到深度处(过程)，继续反向传播被接收换能器接收(过程)，另一部分在缺陷处(即深度处)直接反向传播被接收换能器接收()，两部分最终经声-电转换过程，成为接收电信号。

(3)

由式(2)、(4)可知

所以缺陷响应的解卷积模型为

这里需要说明的是，图1仅仅为了简述区域概念，实际上所说的区域概念并不是图1所示的矩形区域，而是一个以激发点位置为半球中心的声波所历经的某个区域。

2 有限元仿真

2.1 模型构建

实际上，混凝土结构系统由混凝土、波纹管、钢绞线以及水泥浆等部分组成。为了探讨缺陷的不同位置(缺陷的中心位置)及纵向尺寸(方向)对解卷积值的影响，设计了如图3所示的模型，模型尺寸为100 cm×30 cm，内含内径为8.4 cm、壁厚为3 cm的波纹管，中心钢绞线直径为1 cm。模型被均等分成5段，P0-P4，设置了不同类型缺陷，如表1所示。

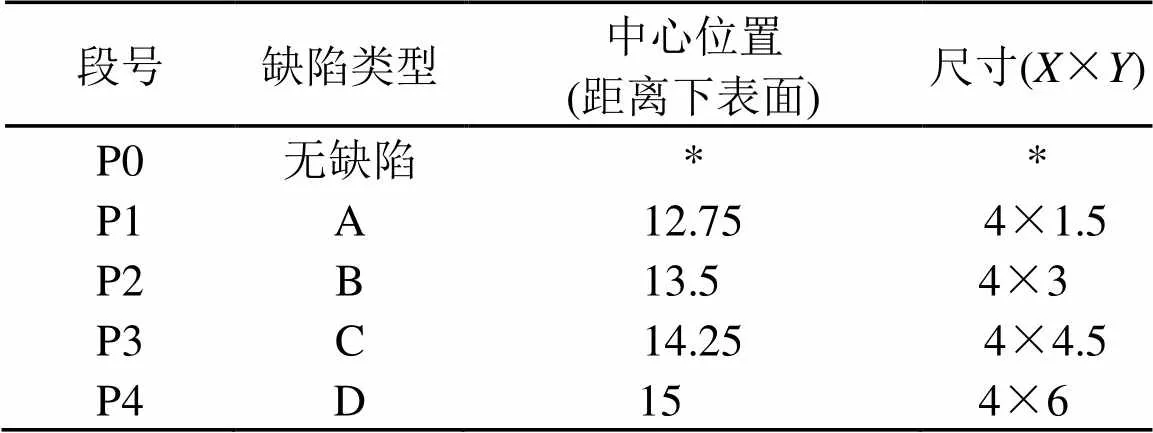
表1 各类型缺陷详情(单位：cm)

对P0-P4等5段模型进行超声检测，检测工作分为两组，第一组：从下表面激发超声波(向正方向激发)，采集回波信号从左至右依次编号为：①②③④⑤。第二组：从上表面激发超声波(向负方向激发)，采集回波信号从左至右依次编号为：⑥⑦⑧⑨⑩。两组检测均采用一发一收模式采集回波信号，收发间隔为2 cm。通过COMSOL Multiphysics仿真软件进行仿真，以线源代替发射换能器(直径1 cm)，接收换能器在相应的接收点接收回波信号。不同介质的具体物理参数详见表2。

激励信号() 选用经汉宁窗函数调制的单音频脉冲信号，在一定程度上可以减小超声导波在结构体中传播时的频散现象给缺陷检测带来的不利影响[9]。激励信号的时频波形如图4所示。

式中：0=10 μs，=200 kHz。

2.2 典型分析

从仿真结果看来，回波信号成分大致包括首波(1)、横波(2)、表面波(3)、反射回波(4-6)以及一些杂波(7)等，如图5所示。直接处理分析整段回波信号将会带来一些误差，这些误差是由激励信号直接沿着表面传到接收换能器的波(1-3)和杂波(7)共同引起的。需要分析的波纹管注浆的信息，主要分布在波纹管附近，所以获取50~160 μs时间内的回波信号进行处理分析，可以排除首波、横波、表面波和杂波的影响。

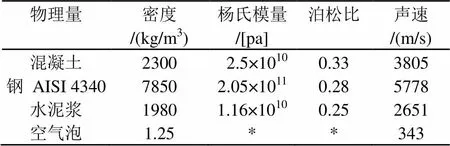
表2 不同物质的物理参数

分析第一组测试相应时间段内的回波信号，它们的时域和频域波形如图6所示。在图6(a)中，60 μs处对应的波的能量较大，它是由波纹管前壁引起的反射回波。160 μs处对应的波是混凝土构件的底面反射回波，含有缺陷特征的信号(由缺陷引起的反射回波)是在处于这两个时间段内，其能量较低，特征仍然十分不明显，难以相互区别。在图6(b)中，回波主要集中在主频200 kHz左右，声波经过混凝土系统后，频率成分较为分散，情况复杂，同样难以区分。第二组测试的波形分析也类似第一组的情况，可见仅通过传统分析法难以直接判断出波纹管压浆情况。

2.3 系统解卷积处理与分析

在两组仿真测试中，将收集到的回波信号进行系统解卷积处理(以P0段信号为参考信号)，得到的结果如图7所示。

解卷积的结果是无缺陷区域系统与含缺陷区域系统的反解结果，即缺陷特征信息。解卷积后的波形的首波是由缺陷引起的响应，这种响应对应的时间(t)是超声波在检测表面与缺陷表面间双程差(2H)的传播时间。在图7(a)中，各个波形的响应时间(t)均是同一时刻，表明各个缺陷的下表面距离检测表面的距离也是相同的。在图7(b)中，各个波形的响应时间(t)均不一样，表明各个缺陷的上表面距离检测表面的距离是不同的，并且可以看出t随着H的增加而增加。

分析可知，不同的缺陷表面距离检测表面的深度(H)与缺陷的响应时间(t)存在一一对应关系。缺陷的表面距离检测表面越近，响应时间就越早；缺陷的表面距离检测表面越远，响应时间就越迟。缺陷表面距离检测表面的距离可由式(8)求得：

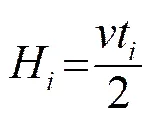
式中，是超声波在混凝土中的纵波波速，3805 m/s[10]。

由式(8)可以求得各个缺陷的上下表面距离检测表面的深度，借此得到各个缺陷的纵向尺寸。若以缺陷的中心作为缺陷的位置，同时也可以给出缺陷的位置，分析结果详见表3。缺陷纵向尺寸的误差率及缺陷位置的误差率均被控制得很低，表明系统解卷积技术在获取缺陷的纵向尺寸及纵向位置方面有着巨大优势。

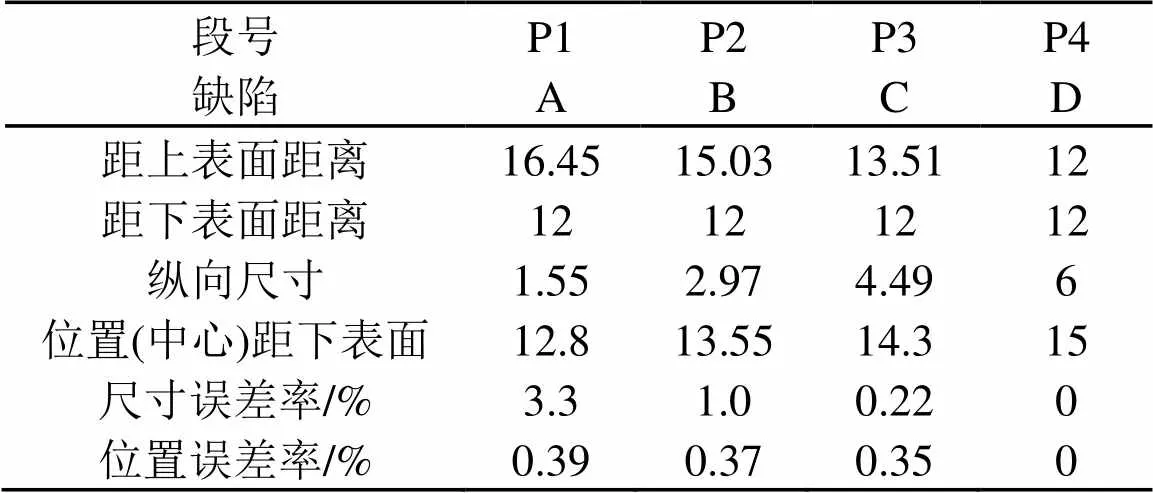
表3 缺陷分析结果数据(单位：cm)

3 现场试验

3.1 模型及测量

为了验证本方法的实际效用，团队为此进行了实测实验。如图8(a)所示，实验模型是一个已经设计好缺陷位置及类型的混凝土试件，内含内径为69 mm、壁厚为3 mm的波纹管。在波纹管内紧贴波纹管壁，预设了截面脱空面积分别为80%、60%、40%、20%等4种类型的空腔缺陷，缺陷详情见表4。

整个模型被分为5段，为了与仿真次序相对应，从右至左依次编号为S0-S4段，每段长为2 m，分别对应压浆密实以及四种缺陷类型，如图8(b)所示。

(a) 混凝土试件

(b) 试件俯视图及测试图

图8 试验模型

Fig.8 An experimental model of concrete component

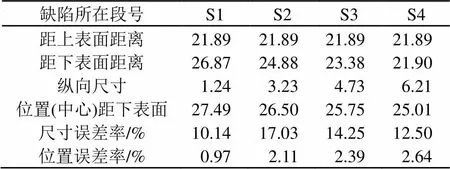
表4 缺陷测试数据(单位：cm)

为了获取缺陷的上下表面信息，检测工作依然分为两组，检测顺序为由右往左，即从图8(b)中的S0段往S4段方向检测。在各段模型检测面的中间处放置激励源，用以激发超声波场，间隔5 cm接收超声回波信号。检测工作中，以自主研发的大功率单脉冲触发器激发超声波，换能器探头的频率为200 kHz，采样频率为1 MHz，采用一发一收模式采集数据。

3.2 结果及分析

如图9所示，任意选取一次测量信号的回波信号，可以看出实测数据与仿真数据具有良好的相似性，由于实际测量过程中总有多种因素的干扰，波形会略有不同。回波信号中的1、2、3号波是发射换能器直接沿着检测表面传给接收换能器的，其强度非常之大，这是后期数据处理的不利因素。而需要分析的波纹管注浆的信息，主要介于100~400 μs时间段内，但是此时间段内的回波信号成分也非常复杂，缺陷引起的回波会淹没在其他回波中，难以在混叠的波形中得到辨别，缺陷信息也难以得到提取，并且在各个测量点所测得的数据波形又极为相似，直接分析比较也变得极为困难。

在图9中，4号波(由波纹管引起的反射回波)的响应时间为108 μs，波纹管前端管壁距离检测表面距离的双程差为43 cm，可得超声波在该混凝土试件中的纵波波速为3981 m/s

实验所得数据为时间-位移序列，利用所述的系统解卷积技术对其进行处理，得到由各缺陷引起的缺陷响应时间，如图10所示。利用式(8)计算得到缺陷尺寸的相关信息，见表4。

通过表4的数据，分析每段模型的解卷积结果的差别，实测数据缺陷纵向尺寸的误差率及缺陷位置的误差率均略有升高，这是由于实际检测过程中存在多种干扰的影响，各段尺寸的纵向误差率均被控制在20%以下，而各段的位置误差率均被控制在3%以下，这些在实际检测中是可以接受的，实测数据得到的结果与理论仿真基本吻合一致。

本研究对规则的单个缺陷进行了仿真与实验，研究表明系统解卷积技术适用于提取缺陷距离检测面的最近距离，并以此判断缺陷的纵向尺寸及位置，其纵向识别分辨率较高，适用于检测结构体中危害性较大的空腔与缺陷。

4 结语

本研究表明系统解卷积后的波形的首波响应时间与该缺陷表面距离检测表面的深度存在一一对应关系，借此可以实现缺陷纵向尺寸及纵向位置的判断。本研究弥补了信息熵等方法在纵向识别方面的不足，由系统角度出发提高了缺陷分辨率，为混凝土结构体的无损检测提供了一套可行技术方案，有利于工程上的监测与维护。

另外，本研究也存在一定局限性。首先，研究假定在单个缺陷情况下，能够得到距离该缺陷表面的距离，但如果存在多个缺陷就不太适用；其次，研究假定不同系统间除了有无缺陷以外其它条件都相同，但实际上其他条件总有差异，这将带来一定的误差，但并不影响时间上的近似判断。

本研究理论上尚不完善，解卷积后的信号虽然带有缺陷信息，但是本研究仅仅得到了首波时间信息，其他方面的信息还有待于进一步深入研究。

[1] Yiching Lin, Mary Sansalone, Nicholas J. Carino. Finite element studies of the impact-echo response of plates containing thin layers and voids[J]. Journal of Nondestructive Evaluation, 1990, 9(1): 27-47.

[2] Ming-Te Liang, Po-Jen Su. Detection of the corrosion damage of rebar in concrete using impact-echo method[J]. Cement and Concrete Research, 2001, 31(10): 1427-1436.

[3] Sansalone M J, Streett W B. Impact-echo[M]. Ithaca, NY: Bullbrier Press, 1997.

[4] Aggelis D G, Shiotani T. Evaluation of grouting in tunnel lining using impact-echo[J]. Tunnelling and Underground Space Technology, 2008, 23: 629-637.

[5] Ninel Ata, Shinichi Mihara, Masayasu Ohtsu. Imaging of ungrouted tendon ducts in prestressed concrete by improved SIBIE [J]. NDT&E International, 2007, 40: 258-264.

[6] CHENG Jin, HANn Qingbang, FAN Honghui. Application of information entropy in the cement grouting test using impact acoustics[C]// Applied Mechanics and Materials, 2014, 584-586: 1217-1223.

[7] 简晓明, 李明轩. 用自适应滤波解卷积进行缺陷类型识别[J]. 声学学报, 1999, 24(6): 637-644.

JIAN Xiaoming, LI Mingxuan. Recognition for defects with adaptive deconvolution[J]. Acta Acustica, 1999, 24(6): 637-644.

[8] Anton I. Lavrentyev, James T. Beals. Ultrasonic measurement of the diffusion bond strength[J]. Ultrasonics, 2000, 38: 513-516.

[9] 王军阵, 王建斌, 王帅. 基于DS89C430的超声导波激励信号源的设计[J]. 电子设计工程, 2010, 10(18): 136-139.

WANG Junzhen, WANG Jianbin, WANG Shuai. Design of signal source for exciting ultrasonic guided wave based on DS89C430[J]. Electronic Design Engineering, 2010, 10(18): 136-139.

[10] 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 3版, 南京: 南京大学出版社, 2012: 337-341.

DU Gonghuan, ZHU Zhemin, GONG Xiufen. Fundamentals of acoustics [M]. 3rdedition, Nanjing: Nanjing University Press. 2012: 337-341.

Nondestructive test method for cement grouting in corrugated pipebased on systemic de-convolution technique

CHENG Jin1, HAN Qing-bang1,2, CHEN Yuan1, FAN Hong-hui3, YIN Cheng1, ZHU Chang-ping1

(1. IOT EngineeringCollege of Hohai University, Changzhou 213022, Jiangsu, China; 2. Huaian Research Institute of Hohai University, Huaian 223001, Jiangsu, China;3. School of Computer Engineering, Jiangsu University of Technology, Changzhou 213001, Jiangsu, China)

A nondestructive test for corrugated pipe based on systemic de-convolution technique is proposed in this paper. The grouting compactness is estimated by this technique through processing the impact echo signals. The positions and size of defects can be obtained by analyzing the beginning time of the head wave in de-convolution results. A model containing 4 different defects is constructed and simulated by using finite element method. The simulation results demonstrate that the complex scattering signals caused by grouting defects are hardly to be distinguished. The collected impact-echo signals are processed by signal processing of systemic de-convolution. It is found that the surface depth of the defect is directly related to the beginning time of the head wave in de-convolution result. Several actual models are constructed and measured, and the results are consistent well with simulated prediction.

system; de-convolution; nondestructive test; finite element; defect

TB553

A

1000-3630(2015)-04-0327-06

10.16300/j.cnki.1000-3630.2015.04.007

2014-07-14;

2014-10-18

国家自然科学基金(11274091、11274092、61302124)、河海大学中央高校基金(2011B11014)、淮安河海研究院开放基金资助项目。

成锦(1989－), 男, 江苏南京人, 硕士, 研究方向为通信与信息系统。

韩庆邦, E-mail: hqb0092@163.com