利用自适应噪声抵消消除工频脉冲干扰仿真

郭英歌，陈晶晶，邹彬彬，王润田



利用自适应噪声抵消消除工频脉冲干扰仿真

郭英歌，陈晶晶，邹彬彬，王润田

(中国科学院声学研究所东海研究站，上海 200032)

介绍一种将自适应噪声抵消算法应用于消除周期性工频脉冲干扰的方法。该方法利用周期sinc函数仿真工频脉冲干扰信号，与白噪声叠加作为参考输入，利用最小均方(Least Mean Square, LMS)算法与归一化最小均方(Normalized Least Mean Square, NLMS)算法进行自适应噪声抵消滤波仿真实验。MATLAB仿真处理结果显示，在无增益、增益饱和、增益过饱和这三种情况下，当信噪比为3 dB时，分别用LMS算法与NLMS算法滤波后可以清晰地分辨多次回波。

自适应噪声抵消；最小均方算法；归一化最小均方算法；工频脉冲干扰

0 引言

在数字电路中得到广泛应用的开关电源的核心是功率转换电路，功率转换电路开关在导通到截止或截止到导通的瞬态过程中，其产生的高速脉冲波形的电流、电压的脉冲上升、下降沿会产生频带较宽即谐波比较丰富的脉冲干扰[1,2]。虽然可以通过电路设计、屏蔽应用等方法压制或避开该噪声，但是仪器设备在采集信号的同时如果需加入时间增益，会使该脉冲干扰随时间增大，从而降低接收信号的信噪比。在声呐及信号探测领域中如浅地层剖面仪由于发射机中的可控硅使用会受到周期性噪声的干扰[3,4]，从而影响探测结果及地层的判读。这种干扰不同于常见的50 Hz工频干扰，但又与工频相关，本文称这种形式的干扰为工频脉冲干扰。此时用简单的带通滤波等方式，会影响到有效信号的保留。自适应噪声抵消技术是基于自适应滤波器原理的一种扩展[5]，它在信号增强技术中是一种有效的降噪方法，若系统能提供良好的参考信号，可获得较好的降噪效果，且信号失真小[6]。这样做的优点是，只需进行后端信号处理，不需要专用硬件便可以实现降噪。本文仿真实验水池环境，产生包括白噪声和工频脉冲干扰的仿真数据，利用自适应抵消算法对不同增益情况下的仿真数据进行处理，并对实验结果进行讨论。

1 算法原理

1.1 自适应噪声抵消原理[7,8]

如图1所示，自适应噪声抵消系统是一个具有二端输入的自适应滤波器，在参考信道输出端的自适应滤波器用来估计噪声，然后从基本信道输入中减去该噪声估计，得到消噪后的信号。

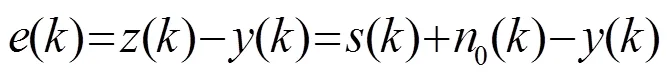
(2)

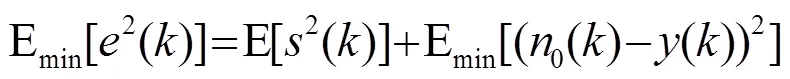
自适应滤波器的调整结果将使()在均方误差最小情况下，最接近实际噪声分量，使得系统输出中的噪声分量大大降低，当滤波器输出()为的最佳估计时，系统输出()为有效信号()的最佳估计。

1.2 最小均方算法

自适应抵消系统的最小均方算法(Least Mean Square, LMS)的迭代公式为[7,8]

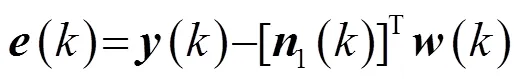
(5)

当步长一定时，在自适应滤波器输入信号较大的情况下会产生梯度噪声放大问题[7,9]，于是提出了归一化最小均方(Normalized Least Mean Square,NLMS)算法。

1.3 归一化最小均方(NLMS)算法

自适应抵消系统的NLMS算法的迭代公式为[7]

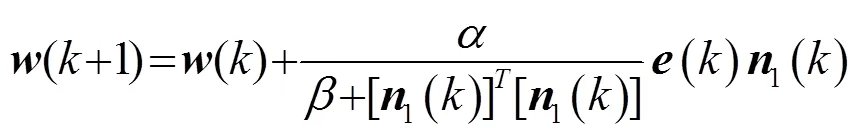
2 自适应噪声抵消仿真

在MATLAB环境下利用LMS与NLMS算法进行自适应噪声抵消仿真实验。本文仿真在深度为6 m的实验水池中进行，声速为1500 m/s。利用GPY2000发射信号时记录的声源信号仿真产生系列回波信号。本文中工频脉冲干扰不是50 Hz的单频信号，而是周期脉冲干扰，所以利用式(7)中sinc函数仿真工频脉冲干扰，其中的取值范围为所有实数。

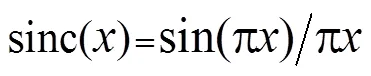
GPY2000的工作频段为1~3 kHz，将仿真信源与干扰通过相应带宽的带通滤波器，从而得到仿真的接收数据。

由于采集到的作为参考输入的噪声中的工频脉冲干扰与原始信号中的工频脉冲干扰相位有可能不同，因此在做自适应噪声抵消滤波前，需要求得并抵消含有工频脉冲干扰的参考信号的时间延时，才能得到较好的滤波结果。

在实际实验中，可以利用声呐探测仪器(如GPY2000)不接负载空发信号或者将发射信号调至很小来采集噪声，将该噪声作为自适应噪声抵消的参考输入。在采集信号有增益时，只需采集一次噪声作为参考输入，在后端处理时加入增益即可。

图2为归一化单帧工频脉冲干扰。在信号中加入均值为0、方差为1的高斯白噪声，产生150帧信号。滤波过程结束后，仿真检波过程，画出如图3所示的二维能量分布图，图中颜色越深的部分表示信号能量越低，黑色即为能量最低处，颜色越浅的部分表示信号能量越高，白色即为能量最高处。之后的二维图表达与之相同。图2为图3的垂向单帧数据。

2.1 接收一次与二次回波信号的工频脉冲噪声消除仿真

在信噪比为3 dB、噪声为白噪声(噪声能量不包括工频脉冲干扰)的情况下，仿真了只接收到一次与二次回波时的原始信号状态，如图4所示。

图4(a)为第75帧归一化含噪原始信号，图4(b)为同帧归一化无噪声回波信号，图4(c)为同帧信号基于LMS算法的自适应噪声抵消归一化结果。可以看出，滤波结果与单帧无噪声回波信号非常相似。程序在处理后一帧信号时，使用的是处理前一帧信号得到的权系数结果，所以在水池这种简单环境中，权系数很快会达到最佳。

图5中纵轴零刻度点为水面，可以看到仿真的两次回波，第一次回波位置为水池池底，已知水池深度为6 m，则深于6 m的部分为地层信息，斜条纹为仿真工频脉冲干扰。该实验通过基于LMS算法的自适应滤波器除去包括工频脉冲干扰与高斯白噪声在内的干扰信号。自适应滤波器阶数取2，步长。从图6中可以看出，通过LMS算法滤波后一次回波与二次回波都可以清晰分辨。

2.2 接收多次回波信号在增益饱和情况下的工频脉冲噪声消除仿真

仿真接收到四次回波，通过窗函数仿真实验设备增益，抵消回波包括传播损失、海底吸收等影响，弥补回波损失，使仿真回波幅值与第一次回波幅度相同，本文称为增益饱和。在噪声为白噪声、信噪比3 dB(噪声能量不包括工频脉冲干扰)的情况下，对输出信号加增益，此时白噪声和工频脉冲噪声也被放大。

图7(a)为第75帧归一化含噪增益饱和原始信号，图7(b)为同帧归一化回波信号，图7(c)为同帧信号基于NLMS算法的自适应噪声抵消归一化结果。可以看出单帧滤波结果与无噪声增益饱和回波非常相似。试验程序处理方法与2.1节相同。

图8为增益饱和后的回波图。在增益饱和时仿真波形中的回波被噪声覆盖无法分辨。通过基于NLMS算法自适应滤波器除去包括工频脉冲干扰与高斯白噪声在内的干扰信号。自适应滤波器阶数取4，步长。得到滤波后的图像如图9所示，从图9可以清晰地分辨出四次回波信号。

图8 增益饱和时仿真原始波形

Fig.8 The simulated original signal with gain saturation

2.3 接收多次回波信号在增益过饱和情况下的工频脉冲噪声消除仿真

本节实验参数与2.2节情况相同，但在弥补多次回波损失时，使多次回波的幅值大于第一次回波，本文称这种情况为增益过饱和。实验中还仿真了设备限幅，即信号幅值的绝对值最大不超过某一固定值。

图10(a)为第75帧归一化含噪增益过饱和原始信号，采样点数随时间增加，在超过某时刻之后信号值被限幅。图10(b)为同帧无噪声归一化增益过饱和回波信号，可明显看出，后到达信号的幅值大于先到达的信号幅值。图10(c)为同帧信号基于NLMS算法的自适应噪声抵消滤波归一化结果。从图10可以，看出滤波结果与单帧无噪声增益过饱和回波信号中各次回波的幅值比例相似。

图11为增益过饱和后的回波信号图。基于NLMS算法自适应噪声抵消仿真程序的参数设置与2.2节相同得到滤波结果如图12所示，从图12中可以清晰地分辨出四次回波信号。

3 结论

本文在实验水池环境下进行了仿真实验，产生了包括白噪声和工频脉冲干扰的仿真数据，利用自适应抵消算法对不同增益情况下的仿真数据进行处理，经过自适应抵消后几次回波能够清楚分辨。

[1] 沈稼树. 高频开关电源中滤波与抗干扰[J]. 通信电源技术, 1997(1): 4-7.

SHEN Jiashu. Filtering ans anti-interference in high frequency switching-mode power supply[J]. The communication power supply technology, 1997(1): 4-7.

[2] 陈涛, 侯振义. 开关电源的干扰及其抑制[J]. 电源技术应用, 2005, 8(11): 55-58.

CHEN Tao, HUO Zhenyi. Electromagnetic interference(EMI) in switching power supply and suppression methods[J]. Power Supply Technologies and Application, 2005, 8(11): 55-58.

[3] 李一保, 张玉芬, 刘玉兰, 等. 浅地层剖面仪在海洋工程中的应用[J]. 工程地球物理学报, 2007, 4(1): 5-8.

LI Yibao, ZHANG Yufen, LIU Yulan, et al. Application of sub-bottom profiler to ocean engineering[J]. Chinese Journal of Engineering Geophysics, 2007, 4(1): 5-8.

[4] 李平, 杜军. 浅地层剖面探测综述[J]. 海洋通报, 2011, 30(3): 344-350.

LI Ping, DU Jun. Review on the probing of sub-bottom profiler[J]. Marine Science Bulletin, 2011, 30(3): 344-350.

[5] 梁鸿翔, 陈晶晶, 王润田. 自适应串扰噪声消除技术在小孔径钻孔超声波检测中的应用[J]. 声学技术, 2009, 28(3): 249-252.

LIANG Hongxiang, CHEN Jingjing, WANG Runtian. Adaptive noise cancelling in small drilling hole detection[J]. Technical Acoustics, 2009, 28(3): 249-252.

[6] 高慧, 牛聪敏, 吴炜. 自适应噪声抵消技术中一种变步长的最小均方(LMS)算法研究[J]. 航天医学与医学工程, 2002, 15(5): 366-368.

GAO Hui, NIU Congmin, WU Wei. A modified mean square(LMS) algorithm with variable step-size for an adaptive noise canceller[J]. Space Medicine & Medical Engineering, 2002, 15(5): 366-368.

[7] 张贤达. 现代信号处理(第二版)[M]. 北京: 清华大学出版社, Springer, 2002: 188-206.

ZHANG Xianda. Modern signal processing(Second Edition)[M]. Beijing: Tsinghua University Press, Springer, 2002: 188-206.

[8] Bernard Widrow. Adaptive noise cancelling: principles and applications[J]. Proceedings of the IEEE, 1975, 63(12): 1692-1716.

[9] 曾召华, 刘贵忠, 赵建平. LMS和归一化LMS算法收敛门限与步长的确定[J]. 电子与信息学报, 2003, 25(11): 1469-1474.

ZENG Zhaohua, LIU Guizhong, ZHASO Jianping. Determining of convergent threshold and step-size of LMS and Normalized LMS algorithm[J]. Journal of Electronics and Information Technology, 2003, 25(11): 1469-1474.

The simulation of using adaptive noise cancellation to eliminate power pulse interference

GUO Ying-ge, CHEN Jing-jing, ZOU Bin-bin, WANG Run-tian

(Shanghai Acoustics Laboratory, The Chinese Academy of Sciences, Shanghai 200032, China)

This paper describes a way of using adaptive noise cancellation to eliminate periodic power pulse interference and others. The method takes periodicpulse signal, which simulates periodic power pulse interfering signal, with white noise as the reference input. The LMS algorithm and NLMS algorithm are used for the simulation of eliminating noise. In the three conditions of no gain, gain saturation and gain oversaturation, the outputs of MATLAB simulations for the input SNR of 3dB show that after using LMS algorithm and NLMS algorithm filtering, multiple echoes can be distinguished clearly.

adaptive noise cancellation; least mean square algorithm; normalized least mean square algorithm; power pulse interference

TB566

A

1000-3630(2015)-04-0342-05

10.16300/j.cnki.1000-3630.2015.04.010

2014-11-11;

2015-03-20

郭英歌(1990－), 女, 新疆人, 硕士, 研究方向为水声信号处理。

郭英歌, E-mail: guoyingge12@mails.ucas.ac.cn