基于身份的动态数字签名方案

张静，权双燕，王伟，孙大宝，蒋椅

（1.东莞职业技术学院继续教育学院，广东 东莞 523808；2.陕西理工学院数学与计算机科学学院，陕西 汉中 723001；3.西安石油大学理学院，陕西 西安 710065；4.西南交通大学电气工程学院，四川 成都 610031）

基于身份的动态数字签名方案

张静1，权双燕2，王伟3,4，孙大宝3，蒋椅3

（1.东莞职业技术学院继续教育学院，广东 东莞 523808；2.陕西理工学院数学与计算机科学学院，陕西 汉中 723001；3.西安石油大学理学院，陕西 西安 710065；4.西南交通大学电气工程学院，四川 成都 610031）

数字签名是解决信息安全问题的重要途径，用于鉴别用户身份.随着计算机、网络的发展，安全的用户数字签名显得尤为重要.目前，现代的数字签名技术正向智能化、密码化、多因素、大容量和快速响应方向发展.结合数论中的中国剩余定理及RSA公钥体制，提出了一种基于身份的动态数字签名方案.

中国剩余定理；动态数字签名方案；身份

DO I：10.3969/j.issn.1008-5513.2015.02.011

1 引言

随着计算机的广泛应用和计算机网络的不断发展，社会呈现出信息化、网络化的发展态势，计算机辅助协同工作（CSCW：com puter supported cooperativework）成为可能并长足发展，而由此引起的计算机系统安全性问题不容忽视［1］.网络固有的开放性、可扩充性，使得其安全问题日趋明显［2-3］.保护信息安全已经成为整个社会的共识，各国都对信息安全系统的建设给予极大的关注与投入.网络信息的安全随着计算机网络的发展而进一步深化和完善.为了防范信息安全风险，新的安全技术和规范不断出现，作为其中关键技术的密码学，近年来也得到很大的发展［4-5］.数字签名作为解决信息安全问题的重要途径，就显得尤为重要［6-7］.

2 预备知识

2.1 公开密钥密码

公开密钥密码就是采用公开的加密密钥和秘密的解密密钥的一种体制.公开的加密密钥简称公开密钥，记为PK；秘密的解密密钥称为秘密密钥，记为SK.任何人都可以用另一个使用者的公开密钥来加密数据，而仅仅是那个知道秘密密钥的使用者才能将加密的数据进行解密.加密算法E和解密算法D可以是不同的，亦可以是相同的.通常，E和D都是公开的.在这种情况下，整个体制的安全核心是SK的保密.因此公开密钥必须具有下列特性：

（1）使用者必须高效地计算出成对的公开密钥和秘密密钥，即PK和SK；

（2）在PK已知的情况下，决不允许从有关PK的知识中有效地推导出SK；

（3）加密之后继之以解密便能恢复原文，即对EPK域中所有M，都有

解密之后继之加密以后也能恢复原文，即对DSK域中所有M，都有

其中EPK是在公开密钥为PK时的加密算法，DSK是在秘密密钥为SK时的解密算法.

RSA公开密钥密码是最重要的公开密钥密码之一，其安全性是基于大整数分解数学问题的难解性.

2.1.1 RSA公钥密码体制

Ron Rivest和Adi Sham ir以及Leonard Adleman于1978年提出的RSA公钥密码体制被认为是一个安全性能良好的密码体制［8］.

RSA公钥密码体制描述如下：

（1）选取两个大素数p和q（保密）.

（2）计算n=pq（公开），ϕ（n）=（p−1）（q−1）（保密）.

（3）随机选取正整数e，1＜e＜ϕ（n），满足gcd（e,ϕ（n））=1，e是公开的加密密钥.

（4）计算d，满足de≡1（modϕ（n）），d是保密的解密密钥.

（5）加密变换：对明文m∈Zn，密文为c=memod n.

（6）解密变换：对密文c∈Zn，明文为m=cdmod n.

2.1.2 RSA的安全性讨论

RSA公钥密码体制的安全性基于大整数的素分解问题的难解性.

尽管尚未在理论上严格证明因子分解问题一定是难解的，但经过长期的研究，迄今没有找到一个有效算法的事实，使得因子分解问题成为众所周知的难题.这是RSA公钥密码体制建立的基础.

从下面的讨论可以看出，破译RSA的明显方法至少和因子分解问题一样困难.

（1）如果密码分析者能够分解n的因子p和q，则就可以容易地求出ϕ（n）和解秘密钥d，从而破译RSA.因此，破译RSA不可能比因子分解问题更困难.

（2）如果密码分析者能够不对n进行因子分解而求得ϕ（n），则可根据de≡1（mod（ϕ（n））求得解密密钥d，从而破译RSA.因为

所以知道ϕ（n）和n就可以容易地求得p和q，从而成功地分解n.因此，不对n进行因子分解而直接计算ϕ（n）并不比对n进行因子分解更容易.

（3）如果密码分析者能够既不对n进行因子分解也不求ϕ（n）而直接求得解密密钥d，则可计算ed−1，ed−1是ϕ（n）的倍数.已知利用ϕ（n）的倍数可以分解出n的因子.因此，直接计算解密密钥d并不比对n进行因子分解更容易.

随着计算能力的持续增长和因子分解算法的不断完善，为保证RSA的安全性，在实际应用中选取得素数p和q越来越大.除了指定n的大小之外，为避免选取容易分解的整数n，研究人员建议对p和q采取如下限制：

（1）p和q的长度应该相差不多；

（2）p−1和q−1都应该包含大的素因子；

（3）gcd（p−1,q−1）应该很小.

2.1.3 中国剩余定理

中国剩余定理是春秋时的孙子最先提出并应用的，因此又称孙子定理.在中国古代的多本数学专著中都有这一问题的描述和解法，最为著名的是唐朝和尚一行提出的解法，称为大衍求一术.

中国剩余定理本质上是求解同余方程组.在现代数论中，中国剩余定理具有十分重要的理论地位与应用价值［9-11］.例如在雷达领域中，中国剩余定理被用在脉冲多普勒雷达上，解目标的距离模糊和速度模糊，在线天线阵接收雷达中解测角的模糊；在信号处理的理论中，基于中国剩余定理的数论变化是一种重要的快速变换方法，只是目前还缺乏对其物理意义的描述而使其应用受到一定的限制；在IC设计中，应用中国剩余定理可以获得高效的IIR滤波器设计的方法.

中国剩余定理：

如果n≥2，而m1,m2,···,mn是两两互素的n个正整数，令

式中

则同时满足同余方程

的正整数解为：

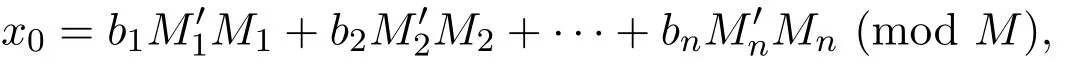
的正整数解，即Mi为mi模的乘逆.

3 基于身份的动态数字签名方案

“动态签名”是与“静态签名”相对而言的，它们的主要区别在于一个“动态签名”只能使用一次，而且每次不同；而“静态签名”则重复多次使用，每次都一样.在签名过程中加入不确定因素，使每次签名过程中传送的信息都不相同，以提高签名过程安全性.系统接收到签名后做一个验算即可验证用户的合法性.

3.1 系统的初始化过程

且di＜IDi，有

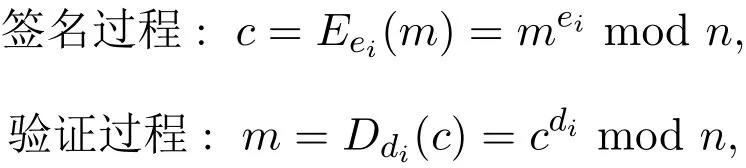
SC利用每个用户的验证密钥di以及IDi（i=1,2,···,n）.求满足同余方程：

的正整数解为：

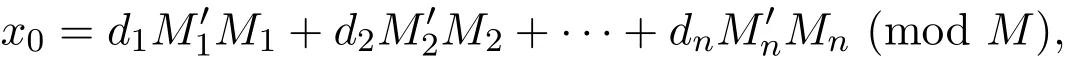
式中，

f是一个双向函数，由a,b可以求得f（a,b），相反由f（a,b）也可求得a,b.系统中的参数总结如下：

（1）SC保留的秘密信息：ϕ（n）,p,q；

（2）系统公开信息：x0,n，双向函数f；

（3）用户ui保留的秘密信息：ei；

（4）用户保留的公开信息：IDi.

3.2 签名过程

假设有一用户ui（i=1,2,···,n）,将要对文章m签名，他提交由身份识别符IDi，时间T和文章m杂凑函数t（m）构成的口令

验证过程：任意用户利用di=x0mod IDi求出用户的验证密钥di，对签名进行验证，求出双向函数值fei（t（m）,T），继而求得t（m）和T，验证T值是否符合要求，若不符合，则表明口令被重播或修改；若符合要求，则验证t（m）是否与用户先前提交的m相关，若相关，则通过验证；若不同，则拒绝该用户.

3.3 安全性及性能分析

（1）口令验证方案中采用了时间标志IDi及T用来鉴别申请用户，又用来防止口令重播.某个用户uj利用原来ui已发送的口令

将T改为T′，即将

以uj的名义进行签名，但因为它不能修改fei（t（m）,T）中的T，所以不能通过验证.

（2）IDi作为身份识别符，还起到了信息隐藏的作用.x0公开，省去了公开di公钥表.

（3）方案采用了RSA公钥密码体制，提供安全性保证.

［1］谭凯军，诸鸿文.一种基于孙子定理的会议密钥的分配机制［J］.小型微型计算机系统，1999，20（3）：181-184.

［2］卢铁成.信息加密技术［M］.成都：四川科学技术出版社，1989.

［3］Bruce Schneier.应用密码学［M］.北京：机械工业出版社，2000.

［4］聂元铭，丘平.网络信息安全技术［M］.北京：科学出版社，2001.

［5］卢开澄.计算机密码学-计算机网络中的数据保密与安全［M］.2nd ed.北京：清华大学出版社，1998.

［6］Goutam Saha，M ina Desai，A rghya Ghosh，et al.Digital Signature M odeling in E-Business［J］.International Conference on E-Business Engineering（ICEBE），2014，DOI：10.1109/ICEBE.2014.67.

［7］Tsujii S，Gotaishi M，Tadaki K，et al.Proposal of a Signature Schem e Based on STS Trapdoor［J］.Post-Quantum Cryptography，2010，6061：201-207.

［8］陈鲁生，沈世镒.现代密码学［M］.北京：科学出版社，2002.

［9］杨世辉.孙子定理探源［J］.涪陵师专学报，2000，16（2）：71-75.

［10］闵嗣鹤，严士健.初等数论［M］.北京：高等教育出版社，2007.

［11］阮传概.近世代数及其应用［M］.北京：北京邮电学院出版社，1988.

2010 M SC：03C65

A dynam ic d igital signatu re schem e on iden tity

Zhang Jing1，Quan Shuangyan2，Wang Wei3，4，Sun Dabao3，Jiang Yi3

（1.Departm ent of Continous Education of Dongguan Polytechnic College，Dongguan 523808，China；2.College of Mathematics and Com puter Science of Shaanxi University of Technology，Hanzhong 723001，China；3.College of Sciences of Xi'an Shiyou University，Xi′an 710065，China；4.College of Electrical Engineering of Southwest JiaoTong University，Chengdu 610031，China）

D igital signature is an im portant way to solve the problem of inform ation security，which used to identify the user's identity.W ith the developm ent of com puter and network，security user digital signature scheme is very im portant.So far，modern digital signature technology is developing to the direction of the intelligentialize，encipherm ent，multi-factor，large capacity and rapid response.In this paper，combining the Chinese rem ainder theorem of the number theory w ith RSA pub lic key schem e，a dynam ic signature schem e on identity is p roposed.

Chinese rem ainder theorem，dynam ic digital signature schem e，identity

O 29；TP393.08

A

1008-5513（2015）02-0204-06

2014-12-19.

国家自然科学基金面上项目（61175055）；中国博士后科学基金面上一等资助项目（2013M 540716）；汉中市科技局专项科研计划项目（2013hzzx41）.

张静（1981-），硕士，讲师，研究方向：信息及编码、密码学.