基于灰色关联熵的进近管制系统风险性研究
张兆宁,金伟伟(中国民航大学国家空管运行安全技术重点实验室,天津300300)
基于灰色关联熵的进近管制系统风险性研究
张兆宁,金伟伟
(中国民航大学国家空管运行安全技术重点实验室,天津300300)
针对进近管制系统运行中的风险性问题,提出运用耗散结构中的熵值理论来研究进近管制系统的风险性。首先,分析进近管制系统运行中的风险,构建风险因素集;然后,在此基础上基于熵值理论对进近管制系统进行耗散结构分析,给出进近管制系统的熵流模型及其灰色关联熵值计算方法,并通过系统熵变来判别系统风险性增减变化;最后,通过分析导致某进近管制中心不安全事件发生的风险因素,验证该方法的可行性。研究表明,把灰色关联熵作为一个参数,能够揭示进近管制系统风险性增减变化的规律。
进近管制系统;风险性;耗散结构;灰色关联熵
进近管制系统作为空管系统的一个子系统衔接着区域管制和塔台管制,是其中一个关键的子系统。由于运行过程中内外安全环境不断变化,危险致因风险来源广等很多不确定性,管制系统运行中会潜伏着各种各样的风险,易发空管不安全事件。如何探索进近管制系统的风险性变化趋势,是空中交通安全管理亟待解决的课题之一。有研究表明,发生在进近管制范围内的空管不安全事件占29%,发生在区域管制范围内的占71%,区域管制范围发生空管不安全事件的绝对值是进近管制的1.82倍,但区域管制范围的空中交通活动总量是进近管制的数十倍,从发生空管不安全事件的相对比率看,进近管制实际上要远远高于区域管制,这表明由于进近管制的空间狭窄、飞行情况复杂,它们是空管不安全事件的易发地带[1]。面对进近管制系统运行中易发空管不安全事件的现实,有必要开展进近管制系统的风险性研究。
在空中交通管理的风险研究中,Peter[2]采用结构化的、系统的方法来评估空管风险;张兆宁等[3]对安全和风险进行了定义,并详细阐述了安全管理和风险管理的关系;丁松滨等[4]认为空中交通系统是一个动态的复杂系统,并运用系统动力学的基本原理和方法对空中交通系统安全管理进行了分析。可见国内外的学者针对空中交通系统的特点提出的风险管理的理论模型和方法等都有一定的实践意义。
进近管制系统是一个动态的复杂系统,系统运行中潜在的风险因素对系统安全运行的影响具有不确定性和随机性,适合运用耗散结构中的熵值来描述这种不确定性和随机性。因此,本文以耗散结构理论为指导,在对进近管制风险的分析和分类的基础上,建立熵流模型,计算出灰色关联熵值,并利用系统熵变来揭示进近管制系统风险性变化的趋势。
1 进近管制风险因素集的构建
进近管制系统是一个复杂开放的系统,其包含人、机、环、管四个子系统,在提供空中交通服务过程中每个子系统都存在着很多对终端区空中交通安全造成威胁的风险。
1.1进近管制风险构成要素
进近管制风险主要与风险因素、风险不安全事件和风险损失紧密相关,这三者构成了进近管制风险的基本要件[5]。其中,风险因素是导致风险不安全事件和风险损失发生的基础和前提。
1.2进近管制风险因素的分类
按进近管制过程中风险的起源,并根据系统工程理论,可将进近管制风险分为人为因素风险、设备因素风险、环境因素风险和管理因素风险。
人为因素风险是指进近管制单位的管制员由于其自身的能力和素质所引起的风险[6],包括指挥中出现错忘漏、精力分配不当、复诵监听不足、违规操作、忽视雷达告警、飞行动态掌握不足、特情处置不力、监控不力、进程单使用不规范、管制员间配合不力、管制员与机组配合失效等。设备因素风险是指进近管制单位在提供导航服务和空中交通服务中的各种设备配置、使用等所引起的风险,包括监视、通信和导航设备缺陷及故障、设备维护不力等。环境因素风险是指进近管制过程中的里外环境对管制员的影响所引起的风险,包括管制室工作环境不好、终端区内高山等障碍物干扰、空中交通流量过大、恶劣天气、不明飞行器或者是飞行动物干扰等,即空域情况不佳、通信环境不佳、气象条件差、工作环境不佳。管理因素风险是指由于组织结构、规章制度建设、技能培训和安全文化建设不足所引发的管制员技能、心理、思想甚至是身体方面出现问题所引起的风险,包括流量管理不合理、工作程序不合理、调配预案存在不足、现场管理不当、排班不合理等。
2 进近管制系统风险性
本文对进近管制系统风险性的研究,主要以耗散结构理论和熵理论为指导,首先对进近管制系统进行耗散结构分析,然后在此基础上引入熵流模型,并给出灰色关联熵值的计算模型。
2.1进近管制系统耗散结构分析
进近管制系统由人、机、环、管四个子系统构成,各个子系统相互联系、相互作用,构成了一个复杂的系统。耗散结构理论指出一个复杂的开放系统,在远离平衡状态时,不断地同外界进行物质、能量和信息交换,从中引入负熵流以减少系统的总熵。复杂系统的各个组成部分之间存在着非线性作用,并在涨落作用下通过自组织和突变形成新的有序的耗散结构[7-10]。首先,进近管制系统是一个开放的系统。进近管制系统运行过程中,管制员利用通信导航监视设备获得终端区的飞行、气象等信息,这些信息又作用于整个管制系统,管制系统提供相应的信息,实现了信息的交换;在能量和物质交换方面,不同情况的飞行信息会对管制系统产生不同的影响,此过程中风险不可避免,如果控制风险避免差错,提供优质的管制服务会产生好的管制服务影响力,这个过程完成了能量和物质的输入和输出。其次,管制系统运行中风险不可避免,风险随着时间的积累和转化,它会远离平衡态,使得管制系统处于不安全运行状态。复杂的进近管制系统内部各要素和子系统之间相互影响、相互制约存在着非线性的关系;另外,进近管制系统还不断受到外界的影响而产生无数个“小涨落”,受到涨落影响,风险达到一定的阀值时,系统就会产生“巨涨落”,使得系统运行安全状态发生突变。因此,进近管制系统是个典型的耗散结构,可以利用耗散结构的熵与系统有序性的关系来研究进近管制系统风险的演化机理。
2.2熵流模型
熵是关于概率分布的的函数[8],可以用来描述系统由风险的存在而导致的无序程度,从而反映系统风险性变化的过程。系统的熵值越大有序程度越低风险性越高,熵值越小有序度越高风险性越低[9]。进近管制系统运行中,四个子系统的风险因素随着时间的积累产生正熵,而系统通过与外界交换信息、物质和能量的过程中,由管制部门的风险管理形成自组织、自适应,产生负熵,正熵和负熵共同影响着系统的风险性。在已识别的风险因素集的基础上,建立进近管制系统熵流模型,通过该模型表明管制系统中的正熵和负熵共同作用,推动着风险性的变化而对系统安全运行造成影响,如图1所示。
在耗散结构理论中,把影响系统整体演化的过程参量称为序参量,它的大小决定了系统有序程度的高低,所以系统的有序程度可以用序参量来表达。“协同论”研究表明,协同导致有序,不协同导致无序,而序参量决定着系统的演化方向[10-11]。基于上述分析,进近管制系统能否安全有序的运行取决于系统的序参量能否协同,对进近管制系统而言就是取决于系统中潜在的风险。
2.3灰色关联熵的计算模型
风险因素对系统结构影响的不确定和发生的不确定性以及很多关系难以确切的定义,使得系统具有灰色特性,基于此本文引入灰色关联熵。系统的序参量就是灰色关联熵[12],其计算过程如下:
设系统安全影响因素的时间序列为
X0={X0(1),X0(2),…,X0(n)}
X1={X1(1),X1(2),…,X1(n)}
X2={X2(1),X2(2),…,X2(n)}
……
Xj={Xj(1),Xj(2),…,Xj(n)}
其中,X0={X0(1),X0(2),…,X0(n)}为进近管制系统的参考序列。
根据公式Δi(k)=|X′0(k)-X′i(k)|,计算出差序列为
Δi(1),Δi(2),…,Δi(n)(i=1,2,…,j)
(2)计算关联系数
关联系数为
(i=1,2,…,j;k=1,2,…,n)
式中:β为分辨系数,β∈(0,1),一般取0.5。
Xi(k)表示为比较数列Xj对参考序列X0在k时刻的关联系数,对其进行归一化处理,有
(3)通过上述研究内容,根据参考文献[13]~[18]提出的熵值计算模型,本文给出了进近管制系统运行中各种风险因素产生的灰色关联正熵计算公式为
系统保障安全因素产生的灰色关联负熵的计算公式为式中:Si(k)为第i个安全影响因素在k时刻产生的熵流值。
(4)由此得到安全影响因素的关联熵矩阵M 为
(5)根据安全影响因素与参考序列的关联度所占的比重构造权重矩阵W=[w1,w2,…,wj],关联度计算公式为
(6)最后得到进近管制系统运行总熵S为
2.4进近管制系统风险性分析
进近管制系统运行过程中正熵和负熵不断地流入,如果设进近管制系统总熵为S,则有
式中:Sp为进近管制系统运行过程中源自于管制员的风险因素、设备的风险因素、环境的风险因素和管理的风险因素所带来的正熵;Sn为进近管制系统运行过程中由系统的风险管理和安全培训所带来的负熵。
耗散结构具有分叉现象,进近管制系统是个耗散结构,因此也具有这种分叉现象,如图2所示。起初,系统内外的环境对风险的影响较小,通过系统风险管理的自组织,可以自发地控制这些风险因素,使进近管制系统处于稳定的安全状态(a段);但随着风险的积累和系统的涨落,此时系统会出现以下3种可能:
(1)当系统总熵S>0时,系统向着不平衡状态演化(b段),当管制系统安全影响因素共同发展的不平衡跃过系统稳定的临界阈值λ0时,进近管制系统的风险发生的可能性大大增加。由熵变模型ΔS=Si(k+1)-Si(k)(ΔS为k~k+1时段,系统受内外安全影响因素影响的熵变),并根据熵变值ΔS的大小可以判断系统风险性变化的方向和稳定程度。当ΔS>0时,系统靠近熵增大产生突变的状态,系统的无序度加大,系统风险性持续增加,处于安全状态恶化的过程中;当ΔS<0时,表示进近管制系统的总熵在减小、有序度增强,风险得到控制,系统处于风险性较低的安全运行状态;当ΔS=0时,表明在一定时间间隔内总熵无变化,系统风险产生的正熵和风险管理产生的负熵一直处于势均力敌的状态。
(2)当系统总熵S<0时,Sn<0且|Sn|>Sp,系统安全管理产生的负熵抑制了风险因素产生正熵的影响,使系统的总熵减小为负值,系统的风险性变化趋势走向有序和稳定(c段)。
(3)当系统总熵S=0时,系统风险演化的有序趋势和无序趋势处于均衡状态,系统整体上暂时处于一种安全平衡临界状态,但随着两者的相互影响以及系统安全影响因素的改变和外界环境的变化,这种临界状态终究会消失,系统要么转向稳定,要么转向失稳。
3 应用实例
根据五个时间段导致某进近管制中心不安全事件发生的风险因素统计数据以及空管专家对该管制中心的风险管理和安全培训的评价,本文得到该进近管制系统安全影响因素统计表,见表1。
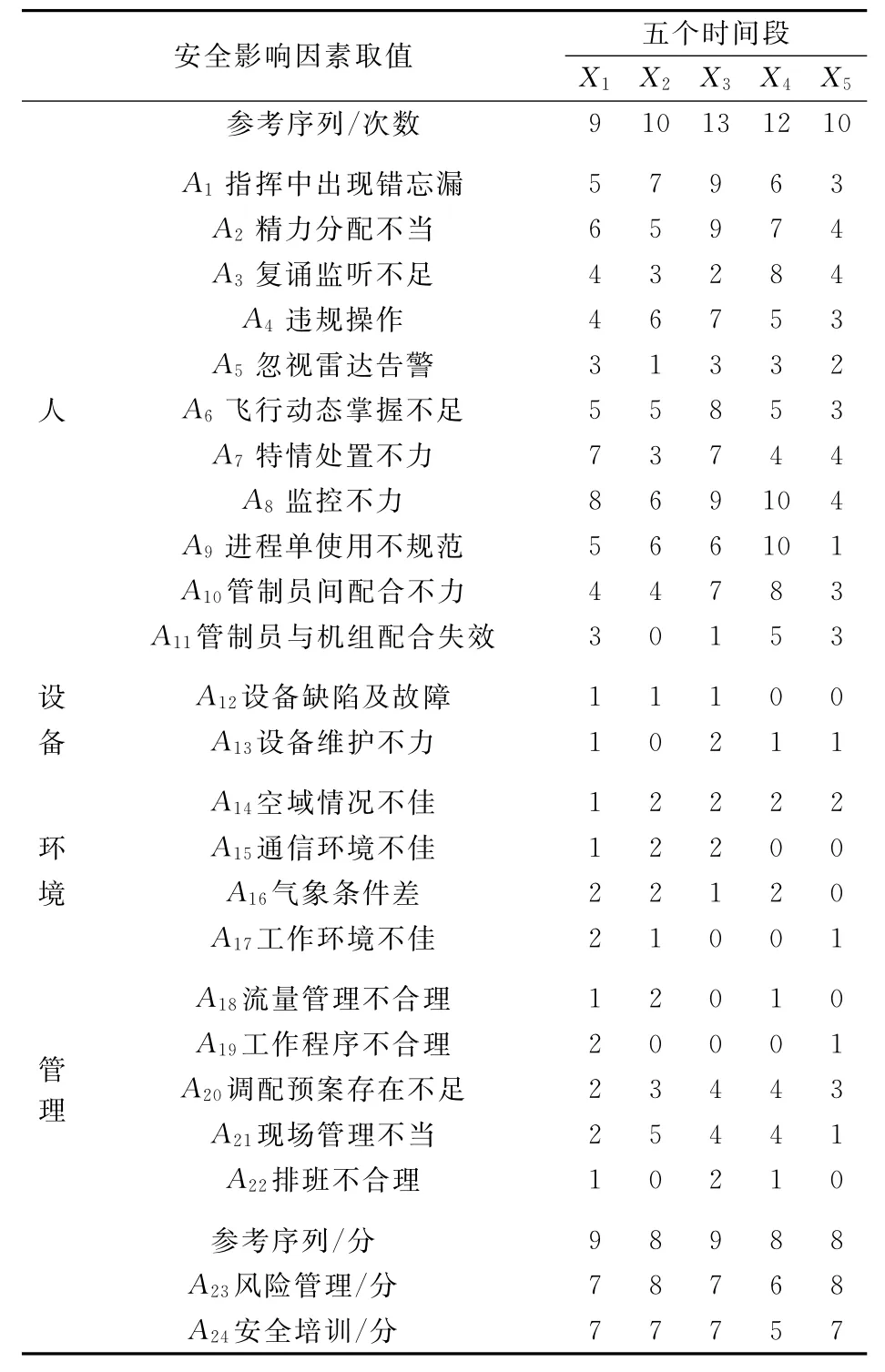
表1 进近管制系统安全影响因素统计表Table 1 Statistical table of safety factors
根据表1各项安全影响因素的数据,按灰色关联熵的计算模型进行如下计算:
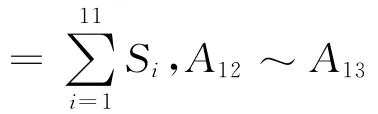
(2)由公式(6)计算出权重系数为
W=(0.390,0.006,0.052,0.052,0.300,0.200)
(3)根据公式(7)计算出该进近管制系统运行总熵S为
S=(1.778,1.767,1.750,1.763,1.762)
由以上计算出来的系统总熵结果,可知不同年份的系统总熵都是大于零的[S(k)>0],表明该进近管制系统运行具有风险性,这也验证了在每年都会发生空管不安全事件,只是有的年份发生的次数多,有的年份发生的次数少这一事实。
由熵变模型ΔS=Si(k+1)-Si(k)可以计算出熵变为-0.011,-0.010,0.013,-0.001。由此可知,该进近管制系统的灰色关联熵值的变化趋势总体上是在减小的,即该进近管制系统运行风险性总的变化趋势是向着减小的方向发展,其中由X3至X4时间段熵变值为0.013,大于0,表明系统风险性在增加,处于安全状态恶化的过程中。由表1也验证了这种变化趋势:X4时间段,风险管理和安全培训的评分是这五个时间段中最低的,且导致不安全事件发生人的风险因素A3、A5、A8、A9、A10、A11也是发生次数最多的,而这些风险因素也是风险管理和安全培训所要重点监控的风险,当其实施的效果不佳时它们的风险性便会增大。说明加强系统的风险管理和管制人员的安全培训,可以有效地控制进近管制系统运行中风险的发生,保障进近管制系统安全有序地运行。
4 结 论
本文在对进近管制系统的风险进行了分析和分类的基础上,以耗散结构理论为指导,对进近管制这个复杂系统进行了耗散结构分析,并通过熵流模型阐明了潜在的风险会增加系统熵,增大系统的风险性;同时,基于熵流模型,针对风险因素的灰色特性,引入灰色关联熵,给出了灰色关联熵值的具体计算方法,并以某进近管制中心发生的不安全事件为例,计算出不同风险因素所产生的熵流值,根据计算结果,分析了该进近管制中心五个时间段的风险性变化趋势。
[1]刘亚军.空管人为因素课题研究[R].中国民航总局空中交通管理局,2002.
[2]Peter S.Risk assessment&mitigation in ATM[J].Safety Science,2006,44(7):629-655.
[3]张兆宁,冯守乐,王莉莉.民航安全管理与风险管理的关系[J].中国民用航空,2011(4):61-63.
[4]丁松滨,石荣,施和平.基于系统动力学的空中交通系统安全管理研究[J].交通运输工程与信息学报,2007,4(4):1-6.
[5]刘堂卿.空中交通管制安全风险耦合机理研究[D].武汉:武汉理工大学,2011.
[6]Reason J.Human error:models and management[J].BMJ,2000,320(7237):768-770.
[7]Shannon C E,Weaver W.The Mathematical Theory of Communication[M].Champaign,Illinois:University of Illinois Press,1959.
[8]Jaynes E T.Information theory and statistical mechanics[J]. Physical Review,1957,106(4):620.
[9]汪送,王瑛,杜纯,等.复杂系统风险熵的涌现与动力学传播分析[J].安全与环境工程,2013,20(2):118-120,134.
[10]王光辉,刘怡君,王红兵.基于耗散结构理论的城市风险形成及演化机理研究[J].城市发展研究,2014,(11):017.
[11]张我华,王军,孙林柱.灾害系统与灾变动力学[M].北京:科学出版社,2011
[12]刘思峰.灰色系统理论及其应用[M].北京:科学出版社,2008.
[13]肖雪梅,王艳辉,张思帅,等.基于耗散结构和熵的高速铁路事故演化机理研究[J].中国安全科学学报,2012,22(5):99.
[14]闫钰.基于耗散结构理论的资产评估系统研究[D].保定:河北农业大学,2006.
[15]杜国梁,高金川,李瑞冬.基于模糊综合评价法和熵值法的泥石流危险度评价[J].安全与环境工程,2013,20(5):15-17,32.
[16]卢立红,张学魁,商靠定,等.信息熵理论在火灾突发事件现场指挥机构设置中的应用[J].安全与环境工程,2011,18(2):65-69,76.
[17]王占武,唐凯,严良.基于熵权TOPSIS法的火电厂选址综合决策[J].安全与环境工程,2011,18(5):103-106.
[18]王亚阳,王汉斌.基于熵值-理想点法的煤矿事故应急资源调配研究[J].安全与环境工程,2014,21(6):135-139.
Study on Approach Control Risk Based on Gray Relational Entropy
ZHANG Zhaoning,JIN Weiwei
(Key State Laboratory of ATC Operation Safety Technology,CAUC,Tianjin 300300,China)
This study proposes to apply the entropy theory from the dissipative structure to studing the risk of approach control system.Eirstly,the paper analyses the approach control system risk and establishes the risk factors collection.Then on the basis of entropy theory,the paper analyses the dissipative structure of approach control system,proposes the entropy flow model for approach control system and its calculation method of gray relational entropy,and determines the change of the system risk by means of the system entropy.Einally,by analyzing the risk factors leading to unsafe events,the rationality of this method is verified.Research shows that taking the gray relation entropy as a parameter can reveal the approach control system risk change rules.
approach control systemic;risk;dissipative structure;gray relational entropy
X949
A
10.13578/j.cnki.issn.1671-1556.2015.05.030
1671-1556(2015)05-0168-05
2015-04-08
2015-08-07
国家自然科学基金项目(71171190);国家空管委科研项目(GKG201410001)
张兆宁(1964—),男,博士后,教授,主要从事空中交通管理方面的研究。E-mail:zzhaoning@263.net

