基于不确定性排放交易模型的空气质量管理

刘 敏，郑川江，陆海清（国网浙江省电力公司电力科学研究院，浙江　杭州310014）

基于不确定性排放交易模型的空气质量管理

刘 敏，郑川江，陆海清
（国网浙江省电力公司电力科学研究院，浙江杭州310014）

点源造成的空气污染已经引起普遍的关注。针对空气质量管理系统存在的多重不确定性与复杂性，基于污染物排放交易规划，研究开发了一个区间随机排放交易（ISET）模型，并应用于空气质量管理问题。开发的ISET模型整合了区间线性规划（ILP）和随机数学规划（SMP）方法，能够处理表示为离散区间数和概率密度函数的多重不确定性以及反映系统复杂性。通过将ISET模型应用到一个假设的空气质量管理案例中，模型应用结果表明:污染物排放交易规划能够实现系统总成本的最小化以及污染物排放速率限值在不同生产企业间的再分配；同时，能够帮助不同生产企业选择合适的污染物控制措施，确定合理的污染物处理量和超标排放量以及污染物排放速率限值分配量，最终生成有效的空气质量管理决策。

空气质量管理；区间随机排放交易（ISE）模型；污染物排放交易规划；区间线性规划；随机数学规划；多重不确定性

随着化石能源（尤其是煤炭）消耗的日益增大，二氧化硫（SO2）和氮氧化物（NOx）等大气污染物排放增加。SO2对人体呼吸器官具有强烈的毒害作用，能够引起不同程度的呼吸道刺激症状，同时它能够破坏植物的叶绿体、损害植物的组织。NOx能够刺激人体肺部，导致肺部构造改变，同时它能够引起植物叶脉间或叶片边缘出现水渍状伤害，导致叶片坏死，并能够破坏臭氧层，改变大气层结构。此外，SO2是酸雨、硫酸型烟雾的重要前驱物，NOx是酸雨、光化学烟雾的重要前驱物，对人类生产和生活产生严重影响。因此，在空气质量管理系统中，运用有效的控制措施和优化方法，构建优化模型，进行污染物排放控制和制定空气质量管理政策尤为重要。

大量的污染物控制措施（包括技术措施、经济政策和法律规范）已经应用于空气质量管理领域。在技术措施方面，石灰石-石膏法、海水法和双碱法等措施运用于SO2处理；选择性催化还原法、选择性非催化还原法和电子束照射法等措施运用于NOx处理。在经济政策方面，污染物排放企业需要支付一定的排污费用，从而间接地促使其控制污染物的排放以节约排污成本。在法律规范方面，污染物排放交易规划运用于空气质量管理问题，以节约污染物处理成本和排放成本，如二氧化碳排放交易规划、氮与磷排放交易规划和废水排放交易规划等已经运用于环境质量管理问题［1-6］。

空气质量管理系统是一个复杂的系统，系统元素具有多重不确定性，从而导致有效管理政策实现的困难。因而，许多研究者提出了一系列不确定性优化方法，以处理系统的复杂性与不确定性［7-15］。如区间线性规划（ILP）方法能够有效地处理系统中存在的、表示为离散区间数的不确定性信息，该方法允许不确定性信息直接与优化过程及输出结果相联系，而且它不会导致复杂的中间子模型，不需要模型参数的分布信息［4］；随机数学规划（SMP）方法能够有效地处理系统中存在的、表示为概率密度函数的随机不确定性信息。上述每种方法仅能够有效地处理表示为单一形式的不确定性信息；然而，为了处理多重不确定性信息以及反映系统复杂性，ILP和SMP方法需要被整合进一个基本的模型框架中，从而导致区间随机规划（ISP）方法的产生。

本文结合不同的污染物控制措施，基于ISP方法和污染物排放交易规划，研究开发了一个区间随机排放交易（ISET）模型，将其应用于空气质量管理问题。开发的ISET模型不仅能够处理表示为离散区间数和概率密度函数的多重不确定性，而且能够反映系统的复杂性。同时，开发一个区间随机排放非交易（ISENT）模型，进行模型间的比较研究。

1　优化模型的构建及求解

在空气质量管理系统中，电力能源以及钢铁、水泥等资源的生产，将产生大量的污染物SO2和NOx，因此需要运用有效的控制措施进行污染物的排放控制。同时，在空气质量管理系统中，许多系统参数具有不确定性以及参数之间的相互关系具有复杂性，污染物控制措施处理效率、经济数据、电能负荷和资源产量等参数不能完全表示为确定值，以及它们的分布信息无法获取，以这类不确定性信息被表示为离散区间数，而污染物产生率是一个随机事件，其不确定性信息被表示为概率密度函数。因此，在空气质量管理系统多重不确定性条件下，需要基于SO2与NOx的排放标准和环境空气质量标准，确定合适的污染物处理措施及处理量，以实现系统成本的最小化。

1.1大气污染物扩散模型

在一定的气象条件下，对于任意的下风向位置，高架连续点源污染物扩散的地面浓度能够通过高斯扩散模型进行评估，模型可表示为［16］

式中:C（x，y）为高架连续点源地面坐标点（x，y）的污染物浓度（mg/m3）；Q为源强，即单位时间内污染物排放量（mg/s）；x为污染源排放点至下风向上任一点的距离（m）；y为烟气中心轴在直角水平方向上到任意点的距离（m）；H为烟囱的有效高度（m）；¯u为平均风速（m/s）；δy为侧向扩散系数，即污染物在y方向分布的标准偏差（m）；δz是竖向扩散系数，污染物在z方向分布的标准偏差（m）。

δy和δz与大气稳定度和水平距离x有关，它们的数值可利用Pasquill-Gifford（P-G）扩散曲线进行估算［16］，或利用《制定地方大气污染物排放标准的技术方法》（GB/T 3840—91）提供的方法进行计算［17］。对于污染物地面浓度，描述单位污染物排放率的转化系数可表示为

从而有

1.2ISET模型的构建

在空气质量管理系统中，污染物排放交易规划被运用，以节约污染物处理成本和排放成本。通过污染物排放交易，每个生产企业的污染物排放量不再受限于各自的污染物排放速率限值，而是总体受限于所有参与污染物排放交易的生产企业的污染物排放速率限值之和；总污染物排放速率限值被重新分配给各个生产企业。因此，基于ILP和SMP两种不确定性优化方法，并结合污染物排放交易规划，ISET模型可表示为

目标函数:

约束条件:

1.3 ISENT模型的构建

在空气质量管理系统中，当污染物排放交易规划未被运用时，每个生产企业的污染物排放量受其各自的污染物排放速率限制。因此，基于ILP和SMP两种不确定性优化方法，ISENT模型可表示为

目标函数:

约束条件:

1.4优化模型的求解

离散区间参数b±可表示为:b±=［b-，b+］= ｛t∈b|b-≤t≤b+｝，其中b-和b+分别为b±确定的下界和上界［18］。因而，首先，基于鲁棒两步法（RTSM）［19］，ISET模型和ISENT模型能够分别转化为两个确定的子模型，这两个子模型分别关联目标函数区间值的上界和下界；其次，利用单纯型法，分别求解关联目标函数区间值上界的子模型（第一子模型）；第三，基于第一子模型的解，利用单纯型法，分别求解关联目标函数区间值下界的子模型（第二子模型）；最后，基于子模型的解，分别形成ISET模型和ISENT模型的解。

2　案例研究

2.1系统概况

本文将上述开发的模型应用于一个假定的、具有不确定性信息的空气质量管理问题。在这个空气质量管理系统中，3个生产企业（火电厂、钢铁厂和水泥厂）排放的污染物SO2和NOx影响着三个敏感区（D1、D2和D3）的空气质量（见图1）。为了控制SO2和NOx的排放以及满足敏感区的环境空气质量标准，每个生产企业分别利用3种SO2控制措施和3种NOx控制措施处理SO2和NOx。因此，研究问题为:①确定合适的SO2和NOx控制措施及处理量，以实现系统总成本的最小化；②分析在不同生产企业间形成的污染物排放交易。

图1　研究系统Eig.1 Study system

表1列出了不同生产企业的污染物控制措施处理效率以及污染物处理与排放相关经济成本。基于研究区域环境质量标准，生产企业一旦排放污染物，便要支付一定的污染物排放费用；基于污染物排放标准，当污染物的排放速率超过其限值时，生产企业需要支付一定的污染物超标排放费用。表2列出了不同污染物的产生情景发生概率和产生率以及生产企业的电能负荷或资源产量。基于研究时期的大气稳定度和平均风速以及水平距离和烟囱有效高度等参数，可以推算得到不同生产企业在敏感区的单位污染物排放率的转化系数见表3。对于火电厂、钢铁厂和水泥厂3个生产企业，SO2的排放速率限值分别为［475，520］×106mg/h、［210，235］×106mg/h和［60，70］×106mg/h，NOx的排放速率限值分别为［175，200］×106mg/h、［83，98］×106mg/h和［38，45］×106mg/h。因而，在研究系统中，总SO2排放速率限值为［745，825］×106mg/h，总NOx排放速率限值为［296，343］×106mg/h。对于D1、D2和D3三个敏感区，SO2的地面浓度限值分别为［0.076，0.086］mg/m3、［0.089，0.099］mg/m3和［0.040，0.050］mg/m3，NOx的地面浓度限值分别为［0.052，0.062］mg/m3、［0.075，0.085］mg/m3和［0.037，0.047］mg/m3。由于系统多重不确定性的存在，数据信息被表示为离散区间数或概率密度函数。此外，假定研究时期的时间跨度均为2 160 h。

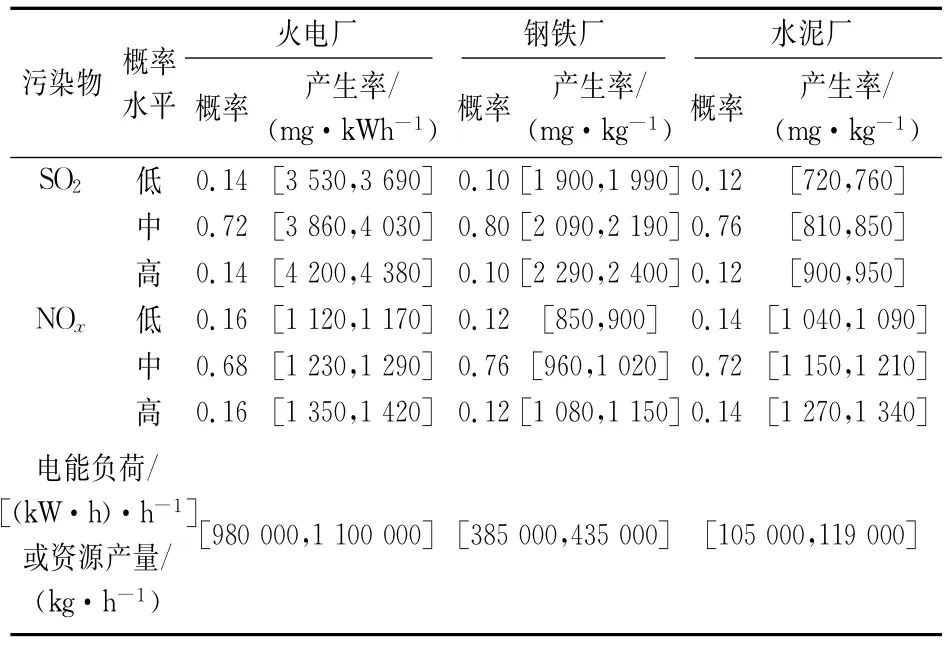
表2　生产企业的污染物产生情景发生概率和产生率以及电能负荷或资源产量Table 2 Probabilities of scenarios occurrence and generation rates for different pollutants and electric power loads and resources amounts for production enterprises

2.2结果分析

表3　生产企业在不同敏感区的单位污染物排放率的转化系数Table 3 Conversion coefficients of unit pollutant emission rate at different production enterprises to sensitive areas

图2　不同生产企业在污染物排放交易规划下再分配的污染物排放速率限值Eig.2 Reallocated limits of pollutants emission rate under pollutants emission trading program for production enterprises

图2为不同生产企业在污染物排放交易规划下再分配的污染物排放速率限值。由图2可见，在污染物排放交易规划和非交易规划下，污染物排放速率限值存在显著的不同。例如，火电厂在排放交易规划下的SO2排放速率限值（623.64×106mg/h）高于其在排放非交易规划下的SO2排放速率限值（［475，520］×106mg/h）；钢铁厂在排放交易规划下的SO2排放速率限值（104.40×106mg/h）低于其在排放非交易规划下的SO2排放速率限值（［210，235］×106mg/h）；水泥厂在排放交易规划下的SO2排放速率限值为［16.96，96.96］×106mg/h，在排放非交易规划下的SO2排放速率限值为［60，70］×106mg/h。上述结果表明:在污染物排放交易规划下，钢铁厂的部分SO2排放速率限值分配给火电厂；水泥厂可能分配部分SO2排放速率限值给火电厂，也可能接受来自钢铁厂的部分SO2排放速率限值。类似地，在污染物排放交易规划下，钢铁厂和水泥厂的部分NOx排放速率限值分配给火电厂。可见，基于污染物排放交易规划，污染物排放速率限值实现了在不同生产企业间的有效分配。

表4列出了生产企业在不同NOx产生概率水平下的NOx超标排放量；然而，在不同SO2产生概率水平下，生产企业的SO2超标排放量均为0 mg/h。由于污染物控制措施的处理效率是有限的，污染物超标排放时有发生；同时，在污染物排放交易规划和非交易规划下，污染物超标排放量是不同的。例如，在污染物排放交易规划和中等NOx产生概率水平下，火电厂、钢铁厂和水泥厂的NOx超标排放量分别为［0，25.08］×106mg/h、［0，50.58］×106mg/h和［0，30.24］×106mg/h；在污染物排放非交易规划和中等NOx产生概率水平下，火电厂、钢铁厂和水泥厂的NOx超标排放量分别为［0，94.61］× 106mg/h、［0，19.05］×106mg/h和0 mg/h。上述结果表明:由于火电厂NOx超标排放的单位成本最高，为减少系统的NOx超标排放成本，在污染物排放交易规划下，面对有限的系统总NOx排放速率限值，水泥厂和钢铁厂将分配部分NOx排放速率限值给火电厂，从而导致火电厂的NOx超标排放量减小以及水泥厂和钢铁厂的NOx超标排放量增加。

表4　生产企业在不同NOx产生概率水平下的NOx超标排放量Table 4 Excess emission amounts of NOxunder different probability levels of NOxgeneration for production enterprises

表5　生产企业在污染物排放交易规划下的污染物处理量和系统总成本Table 5 Treatment amounts of pollutants for production enterprises and total system cost under pollutants emission trading program

表6　生产企业在污染物排放非交易规划下的污染物处理量和系统总成本Table 6 Treatment amounts of pollutants for production enterprises and total system cost under pollutants emission non-trading program

表5和表6分别列出了不同生产企业在污染物排放交易规划和非交易规划下的污染物处理量和系统总成本。由表5和表6可见，在污染物排放交易规划和非交易规划下，生产企业利用不同控制措施处理污染物的处理量存在显著的差异。例如，在污染物排放交易规划和低SO2产生概率水平下，火电厂采用措施S11和S13处理SO2，处理量分别为［470.18，1 069.78］×106mg/h和2 989.23×106mg/h；钢铁厂采用措施S21和S23处理SO2，处理量分别为［612.60，746.75］×106mg/h和118.90× 106mg/h；水泥厂采用措施S31和S32处理SO2，处理量分别为［33.21，48.05］×106mg/h和42.39×106mg/h。在污染物排放非交易规划和低SO2产生概率水平下，火电厂采用措施S11和S13处理SO2，处理量分别为［1 956.60，2 556.20］×106mg/h和1 502.80×106mg/h；钢铁厂采用措施S21和S23处理SO2，处理量分别为［482.08，616.23］×106mg/h 和249.42×106mg/h；水泥厂仅采用措施S33处理SO2，处理量为［75.60，90.44］×106mg/h。SO2处理结果表明:不同生产企业的SO2控制措施处理效率及单位处理成本是不同的，较高的处理效率对应于较高的单位处理成本；在污染物排放交易规划下，有的生产企业（水泥厂）增加较高处理效率控制措施的SO2处理量，并将剩余的SO2排放速率限值分配给其他生产企业（火电厂和钢铁厂），以降低它们的较高处理效率控制措施的SO2处理量和降低SO2处理成本，进而降低整个系统的SO2处理成本。在高NOx产生概率水平下，基于污染物排放交易规划和非交易规划，火电厂均采用措施N11处理NOx，处理量为［1 323.00，1 562.00］×106mg/h；钢铁厂均采用措施N21处理NOx，处理量为［415.80，500.25］×106mg/h。在污染物排放交易规划和高NOx产生概率水平下，水泥厂采用措施N33处理 NOx，处理量为［133.35，159.46］×106mg/h；在污染物排放非交易规划和高NOx产生概率水平下，水泥厂采用措施N31和N33处理NOx，处理量分别为［92.93，119.04］×106mg/h和40.42×106mg/h。NOx处理结果表明:在污染物排放交易规划下，有的生产企业（水泥厂）增加较高处理效率控制措施的NOx处理量，并将剩余的NOx排放速率限值分配给其他生产企业（火电厂），以降低它的NOx超标排放成本，进而降低整个系统的NOx处理与排放成本。在其他情景下，污染物处理具有类似的分析。因而，在整个系统中，考虑污染物排放交易规划，基于污染物控制措施的处理效率以及污染物单位处理成本和超标排放单位成本，生产企业确定合适的污染物控制措施和处理量，以降低污染物处理与排放成本。

由表5和表6可见:系统总成本被表示为区间值，如果变量的实际值在其区间的上下界范围内变动，那么系统总成本也将相应地在其区间的上下界范围内变化；污染物排放交易规划下的系统总成本（［340.17，495.94］×105元）低于污染物排放非交易规划下的系统总成本（［341.07，504.29］×105元），因此在污染物排放交易规划下，污染物排放速率限值能够再分配给具有高污染物超标排放单位成本或高污染物处理单位成本的生产企业，或者剩余的污染物排放速率限值分配给具有污染物超标排放的生产企业。在污染物排放交易规划下，系统总成本是在未考虑污染物排放交易成本的条件下获得的；然而，在一个交易系统中，有时需要考虑不同生产企业间的污染物排放交易成本［20-21］，且随着污染物排放交易成本的增大，系统总成本也将增大。

3　结 论

本文基于污染物排放交易规划，开发了一个ISET模型应用于空气质量管理问题。开发的ISET模型整合ILP和SMP方法到基本的模型框架中，模型与方法是一个简单和有效的管理工具。在空气质量管理系统中，ISET模型不仅能够处理表示为离散区间数和概率密度函数的多重不确定性，而且能够反映系统的复杂性，并且模型结果是确定性的、区间的及随机信息的组合，能够实现空气质量管理的多种决策选择。

将开发的ISET模型应用到一个假设的空气质量管理案例中，应用结果表明:污染物排放交易规划能够实现系统总成本的最小化以及污染物排放速率限值在不同生产企业间的再分配，同时能够帮助生产企业实现污染物控制措施的选择以及确定污染物处理量、污染物超标排放量和污染物排放速率限值分配量，最终生成有效的空气质量管理决策。

［1］Horan R D，Abler D G，Shortle J S，et al.Cost-effective pointnonpoint trading:an application to the Susquehanna River Basin ［J］.Journal of the American Water Resources Association，2002，38（2）:467-477.

［2］Luo B，Maqsood I，Huang G H，et al.An inexact fuzzy two-stage stochastic model for quantifying the efficiency of nonpoint source effluent trading under uncertainty［J］.Science of the Total Environment，2005，347（1/2/3）:21-34.

［3］Nahorski Z，Horabik J.Greenhouse gas emission permit trading with different uncertainties in emission sources［J］.Journal of Energy Engineering-ASCE，2008，134（2）:47-52.

［4］Chen W T，Li Y P，Huang G H，et al.A two-stage inexact-stochastic programming model for planning carbon dioxide emission trading under uncertainty［J］.Applied Energy，2010，87（3）: 1033-1047.

［5］Li M W，Li Y P，Huang G H.An interval-fuzzy two-stage stochastic programming model for planning carbon dioxide trading under uncertainty［J］.Energy，2011，36（9）:5677-5689.

［6］Corrales J，Naja G M，Bhat M G，et al.Modeling a phosphorus credit trading program in an agricultural watershed［J］.Journalof Environmental Management，2014，143:162-172.

［7］Liu L，Huang G H，Liu Y，et al.A fuzzy-stochastic robust programming model for regional air quality management under uncertainty［J］.Engineering Optimization，2003，35（2）:177-199.

［8］Li Y P，Huang G H，Veawab A，et al.Two-stage fuzzy-stochastic robust programming:A hybrid model for regional air quality management［J］.Journal of the Air and Waste Management Association，2006，56（8）:1070-1082.

［9］An H，Eheart J W.A screening technique for joint chance-constrained programming for air-quality management［J］.Operations Research，2007，55:792-798.

［10］Chan K Y，Papalambros P Y，Skerlos S J.A method for reliability-based optimization with multiple non-normal stochastic parameters:a simplified airshed management study［J］.Stochastic Environmental Research and Risk Assessment，2010，24（1）:101-116.

［11］邱兆文，邓顺熙，郝艳召.基于AERMOD模型评估公路交通源PM2.5的浓度分布［J］.安全与环境工程，2014，21（3）:65-69.

［12］Ping J，Chen B，Husain T.Risk assessment of ambient air quality by stochastic-based fuzzy approaches［J］.Environmental Engineering Science，2010，27（3）:233-246.

［13］Lv Y，Huang G H，Li Y P，et al.Development of a sequential decision-making model for controlling multiple air pollutants under uncertainty［J］.Water Air and Soil Pollution，2012，223（1）: 443-465.

［14］Wang S，Huang G H.A coupled factorial-analysis-based interval programming approach and its application to air quality management［J］.Journal of the Air and Waste Management Association，2013，63（2）:179-189.

［15］Shao L G，Xu Y，Huang G H.An inexact double-sided chanceconstrained model for air quality management in Nanshan District，Shengzhen，China［J］.Engineering Optimization，2014，46 （12）:1694-1708.

［16］蒋展鹏.环境工程学［M］.2版.北京:高等教育出版社，2005.

［17］国家技术监督局，国家环境保护局.GB/T 3840—91 制定地方大气污染物排放标准的技术方法［S］.北京:中国标准出版社，1991.

［18］Huang G H.IPWM:An interval parameter water quality management model［J］.Engineering Optimization，1996，26（2）:79-103.

［19］Ean Y R，Huang G H.A robust two-step method for solving interval linear programming problems within an environmental management context［J］.Journal of Environmental Informatics，2012，19（1）:1-9.

［20］Luo B，You J S.A watershed-simulation and hybrid optimization modeling approach for water-quality trading in soil erosion control［J］.Advances in Water Resources，2007，30（9）:1902-1913.

［21］Wang Y H.A simulation of water markets with transaction cost ［J］.Agricultural Water Management，2012，103:54-61.

An Uncertain Emission Trading Model for Air Quality Management

LIU Min，ZHENG Chuanjiang，LU Haiqing
（Electric Power Research Institute，State Grid Zhejiang Electric Power Company，Hangzhou 310014，China）

Air pollution from point source has aroused widespread concerns.In air quality management systems，due to the existence of multiple uncertainties and system complexities，the study develops an interval stochastic emission trading（ISET）model to achieve effective air quality management policy making on the basis of the pollutants emission trading program，the developed ISET model，incorporating interval linear programming（ILP）and stochastic mathematical programming（SMP）methods，can deal with multiple uncertainties，as disperse interval numbers and probability density function，and reflect system complexities. The study applies the ISET model to a hypothetical case study of air quality management.The results indicate that the pollutants emission trading program can minimize the system cost and reallocate pollutants emission rate limits among different production enterprises；moreover，the program can help different enterprises select the appropriate control measures of pollutants，and determine the reasonable treatment amounts and exceed emission amounts of pollutants as well as the reallocation amounts of pollutants emission rate limits，and ultimately achieve effective air quality management policies.

air quality management；interval stochastic emission trading（ISET）model；pollutants emission trading program；interval linear programming（ILP）；stochastic mathematical programming（SMP）；multiple uncertainties

X51

A

10.13578/j.cnki.issn.1671-1556.2015.05.005

1671-1556（2015）05-0025-08

2015-01-02

2015-03-12

刘 敏（1986—），男，硕士，工程师，主要从事电厂环保工作。E-mail:liumin-224@163.com