具有广义凸性的一类半无限向量分式规划的鞍点准则*
李 钰 ,严建军,李江荣
(1.延安大学 数学与计算机科学学院,陕西 延安716000;2.延安职业技术学院,陕西 延安716000)
近些年,最优化在理论上的相关研究已取得了很大进展,同时,凸性理论也被广泛应用到最优化的各个领域中,而数学规划作为最优化的一个重要分支,影响则更为深远。Preda[1]引入了(F,ρ)-凸函数。Xu[2]对之进行了推广,建立了广义的(F,ρ)- 凸函数。Z. A. Liang,H. X. Huang 和P. M.Pardalos[3]建立了更为广义的凸性条件,提出(F,α,ρ,d)- 凸函数。
本文利用局部渐近锥K,在已有定义(F,α,ρ,d)K- V - 凸函数、(F,α,ρ,d)K- V - 伪凸函数等广义凸函数的基础上,研究涉及这些广义凸性的一类半无限向量分式规划的鞍点准则。
1 基本概念
定义1.1[4]映射K:2X× X →2X称为局部渐近锥,若对每一个集M ⊆X 和每一点x ∈X,锥K(M,x)具有以下性质:
(i)K(M,x)= K(M - x,0);
(iv)K(M,x)= M,对∀x ∈int M;
(v)K(φ(M),φ(x))= φ(K(M,x)),这里φ:X →X 为任一线性同胚;
(vi)O+M ⊆O+K(M,x)。
定义1.2[4]设K(·,·)为一局部渐近锥,则称fK(x;·):X × X →R ∪{+ ∞},为f 在x 处的K - 方向导数。
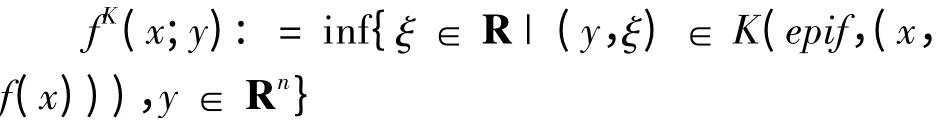
定义1.3[5]若存在紧凸集∂Kf(x),满足fK(x;y)则称f:X →R 在x 处是K -次可微的,其中,对∀y ∈Rn}为f 在x 处的K - 次微分。
定义1.4 称泛函F:Rn× Rn× Rm→R 是次线性的,如果对∀x1,x2∈Rn,有
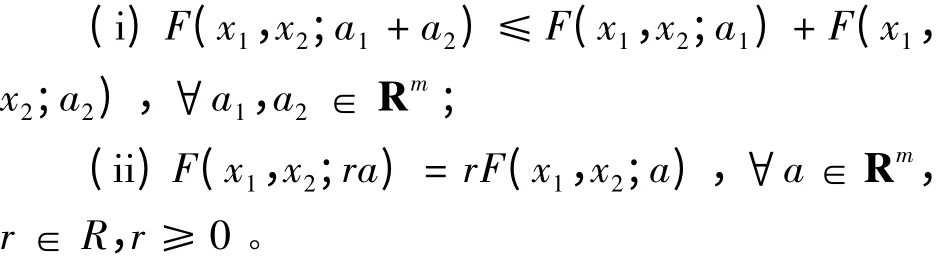
定义1.5[6]设f 是定义在非空开集X ⊂Rn上的实向量函数,f:X →Rp,其每个分量fi是局部Lipschitz 连续的,如果∃F:X×X×Rn→R 是次线性函数,函数α = (α1,…,αp)Τ,αi:X × X →R+{0},d:X × X →R,ρ = (ρ1,…,ρp)Τ,ρi∈R 和局部渐近锥K,如果对于∀x ∈X,有
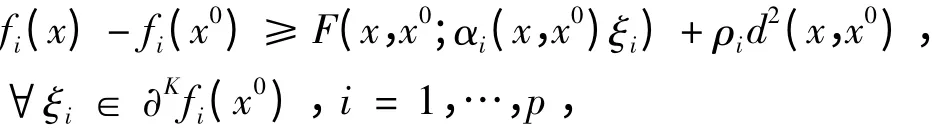
则称f = (f1,…,fp)在x0∈X 处是(F,α,ρ,d)K-V - 凸的。
定义1.6[7]设f 是定义在非空开集X ⊂Rn上的实向量函数,f:X →Rp,其每个分量fi是局部Lipschitz 连续的,如果∃F:X×X×Rn→R 是次线性函数,函数α = (α1,…,αp)Τ,αi:X × X →R+{0},d:X × X →R,ρ = (ρ1,…,ρp)Τ,ρi∈R 和局部渐近锥K,如果对于∀x ∈X,有

则称f = (f1,…,fp)在x0∈X 处是(F,α,ρ,d)K-V - 伪凸的。
定义1.7 设f 是定义在非空开集X ⊂Rn上的实向量函数,f:X →Rp,其每个分量fi是局部Lipschitz 连续的,如果∃F:X×X×Rn→R 是次线性函数,函数α = (α1,…,αp)Τ,αi:X × X →R+{0},d:X × X →R,ρ = (ρ1,…,ρp)Τ,ρi∈R 和局部渐近锥K,如果对于∀x ∈X,有
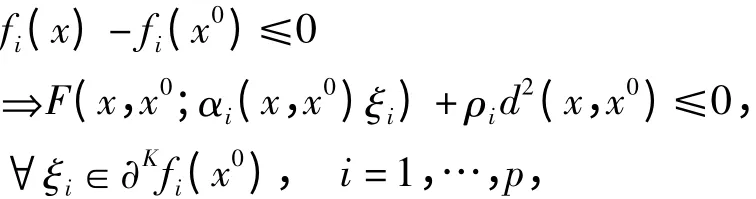
则称f = (f1,…,fp)在x0∈X 处是(F,α,ρ,d)K-V - 拟凸的。
2 主要结果
考虑半无限向量分式规划:
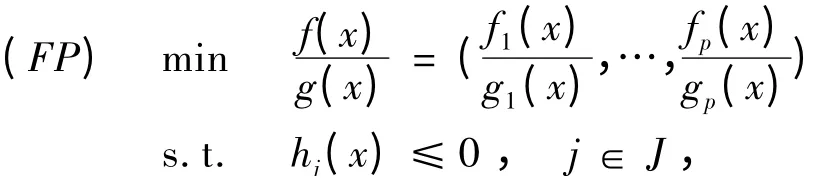
其中fi,gi:X0→R,i = 1,…,p,hj:X0→R,j ∈J,J 为无限紧集,X0⊂Rn是一非空开集。记X ={x ∈X0| hj(x)≤0,j ∈J},J(x*)= {j ∈J |hj(x*)= 0}是主动约束集,R(J)+= {μ:J →R+|对∀j ∈J,仅有有限个μj≠0}。总是假定对所有x∈X0,有fi(x)≥0,gi(x)>0,i=1,…,p。
定义2.1 (FP)的一个可行解x*∈X 称为是(FP)的一个有效解,如果不存在x ∈X,使得
定义2.2 (FP)的一个可行解x*∈X 称为是(FP)的一个弱有效解,如果不存在x ∈X,使得
首先考虑单目标规划问题
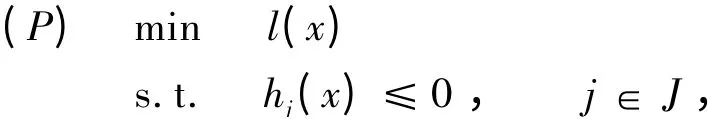
其中l,hj:X0→R 是局部Lipschitz 连续函数。
在点x*∈X0处,记J*={j∈J|hj(x*)=0}。
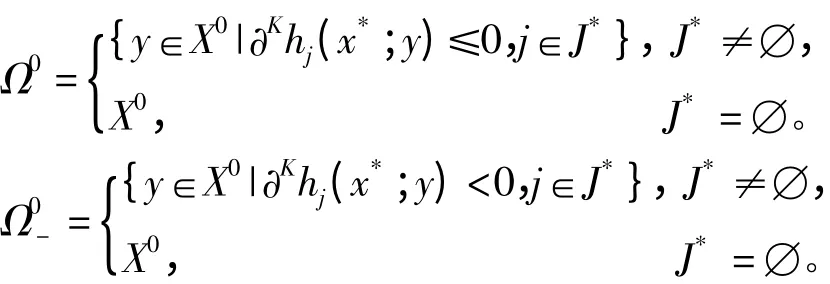
定义2.3 对于问题(P),若在点x*∈X0处,有Ω0-≠∅,则称问题(P)的约束满足约束品性C0。引理2.1[8]若x*是(P)的局部最小点且在x*处(P)的约束满足约束品性C0,则存在数(λj)j∈J,使得
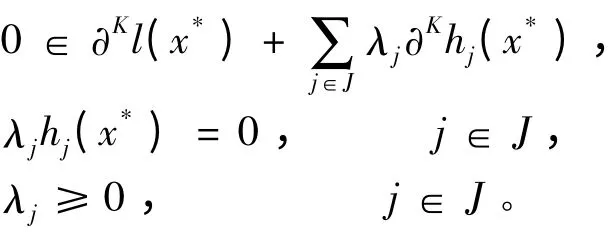
引理2.2[1]x*是(FP)的有效解的充要条件是x*是P 个规划问题(FPk)(k = 1,…,p)的最优解,其中(FPk)为
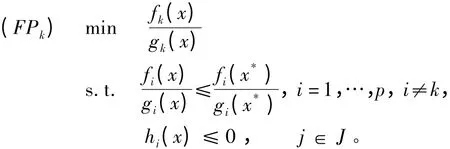
现引入与 (FPk) 有密切关系的规划(EFPk):
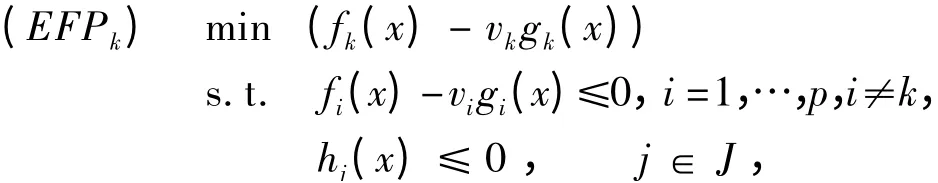
注:易知(FPk)与(EFPk)的可行集相同,均记为D。
引理2.3 x*是(FPk)的最优解的充要条件是x*是(EFPk)的最优解。
引理2.4 若x*是(FPk)的最优解且(EFPk)在x*处满足约束品性C0,则存在非负数τi(i = 1,…,p,i ≠k),(λj)j∈J,使下面各式成立
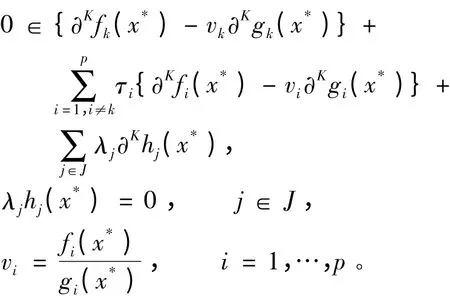
记f(x)= (f1(x),…,fp(x))Τ,
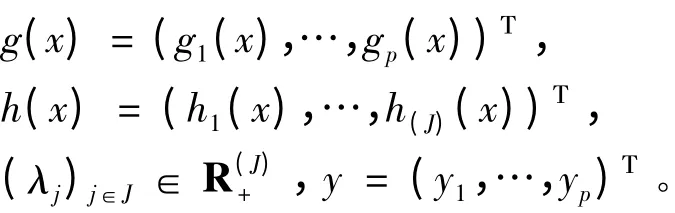
进而考虑与规划(FP)密切相关的参数规划问题
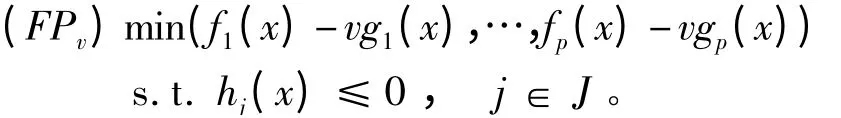
定义2. 4 对应于问题(FP)的Lagrange 函数定义为L(x,y,λ)=,称)是L(x,y,λ)的鞍点,如果对于= 1}及,有
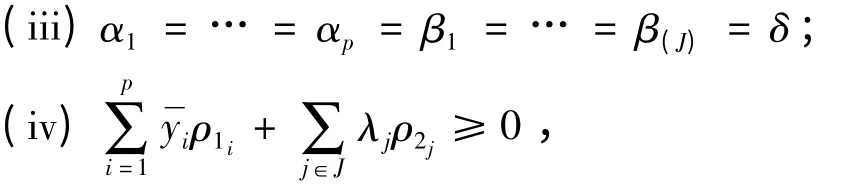
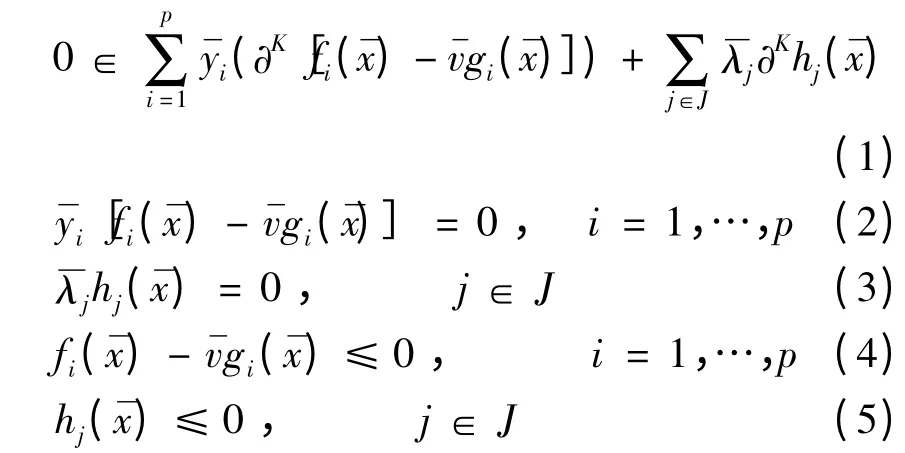

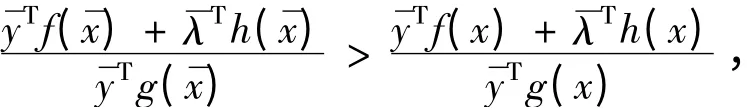
即
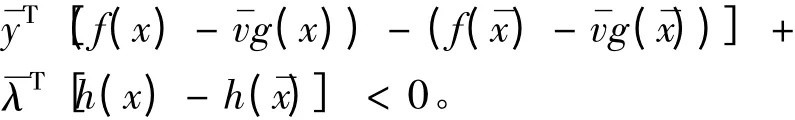
由(i)得
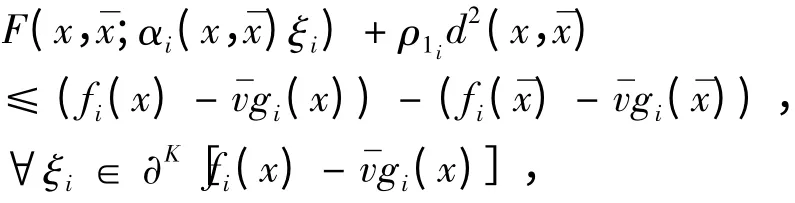
则
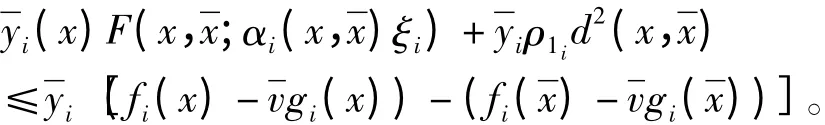
又由(ii)得
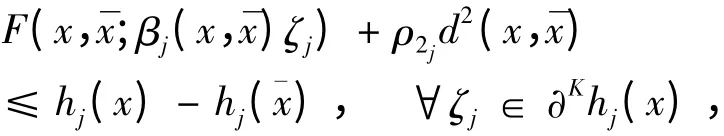
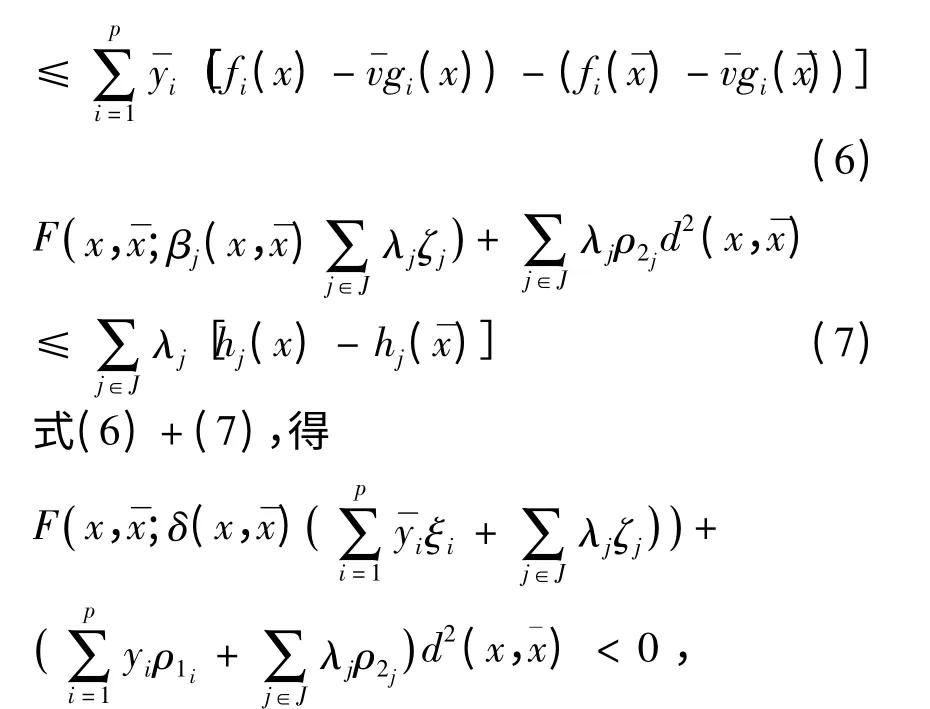
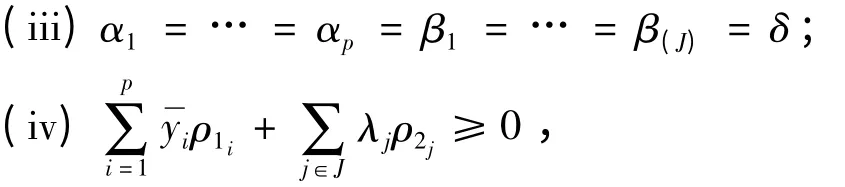
证明 与文献[10]中证明类似。
[1]Preda V. On efficiency and duality for multiobjective programs[J]. Journal of Mathematical Analysis and Applications,1992,166:365 -377.
[2]Xu Z. Mixed type duality in multiobjective programming[J].Journal of Mathematical Analysis and Applications,1996,198:621 -635.
[3]Liang Z A,Huang H X,Pardalos P M. Optimality conditions and duality for a class of nonlinear fractional programming problems[J]. Journal of Optimization Theory and Application,2001,110(3):611 -619.
[4]Elster K H,Thierfelder J. On cone approximations and generalized directional derivatives[M]//Clarke F H,Demyanov V F,Giannessi F. Nonsmooth optimization and related topics. New York:Springer US,1989:133 -159.
[5]Marco castellani. Nonsmooth invex functions and sufficient optimality conditions[J].Journal of Mathematical Analysis and Applications,2001,255(1):319 -332.
[6]李钰,张庆祥,严建军,等. (F,α,ρ,d)K-V -凸半无限分式规划的最优性条件[J].江西科学,2009,27(1):31 -35.
[7]李钰,张庆祥,严建军,等.一类广义半无限向量分式规划的最优性条件[J].河南科学,2009,27(2):132 -136.
[8]Shimizu K,Ishizuka Y,Bard J E. Nondifferentiable and two-level mathematical programming[M].Boston:Kluwer Academic,1997.
[9]Liu J C. Optimality and duality for generalized fractional programming involving nonsmooth pseudoinvex function[J]. Journal of Mathematical Analysis and Application,1996(220):667 -685.
[10]Bector C R. Duality in nonlinear fractional programming[J].Zeitschrift für Operations Research,1973,17:183 -193.

