农业科技投入对减缓农村地区贫困的效果评价——以湖南省国家级贫困县为例

陈　鸣周发明（南华大学经济管理学院，湖南衡阳400；湖南农业大学经济学院；湖南长沙408）



农业科技投入对减缓农村地区贫困的效果评价
——以湖南省国家级贫困县为例

1，2陈鸣2周发明
（1南华大学经济管理学院，湖南衡阳421001；2湖南农业大学经济学院；湖南长沙410128）

文章以湖南省2012年20个国家级贫困县数据为样本，应用三阶段DEA模型，对各县域剔除环境因素、随机误差影响前后的农业科技投入对于农村贫困作用的效果进行了测度和分析。研究发现，加大农业科技投入仍然是湖南各县减贫的关键，且湖南应根据各地区效率差异采取不同导向政策。另外，政府财政补贴的增加与金融发展，并不利于减贫的改进，反而加剧贫富差距；而宏观经济的持续快速扩张以及对教育、医疗、信息化等公共服务的投入则能有效改善农村贫困。

湖南省；县域；农业科技；减贫；三阶段DEA

一、引言

贫困问题是当前中国社会发展和经济建设需要面临的重大挑战。科技作为先进生产要素的代表，对于促进农民增收、减缓贫困具有举足轻重的作用。中国政府历来把科技减贫作为扶贫工作的重要内容。从1986年提出扶贫开发战略，到八七扶贫攻坚计划，再到两个十年的《中国农村扶贫开发纲要》，均突出强调了科技对于减缓贫困的意义，指出技术进步是农村地区脱贫致富的根本途径。可以预料的是，随着我国市场经济体制的进一步完善，制度变革等其他减贫因素带来的作用将越来越有限，未来科技在减贫工作中将承担更大的任务。尽管我国减贫工作取得了实质性的进展，但依然存在脱贫难度加大、减贫效率低下等突出问题。如何适应新时期科技反贫困工作的需要，改革和优化科技减贫体制，提高科技减贫效率，是现阶段减贫工作需要迫切解答的问题。

贫困问题一直以来是学术界关注的焦点。近年来越来越多的文献涉及到农业科技投入对减贫作用的研究领域［1］。就对科技减贫效果的研究文献而言，大致可分为定性与定量两个层面。一些学者对科技减贫的成效进行了定性评价。Alstonet等认为农业科技投入不仅经济回报可观，还可以有效地促进农村减贫［2］。而Reddy，Gu-nasena等认为，要保证科技有效减贫，必须缩小收入差距和不平等程度［3］［4］。Keijiro和Otsuka则认为由于当前制度环境的缺陷，科技并不能有效改善贫困［5］。陈来生等对青海省东部山区化隆县沙连堡乡40项农业科技减贫技术措施进行了打分、汇总、排序、综合分析和评价，肯定了科技减贫效果［6］；汪三贵等通过对河北省平山县、甘肃省会宁县和云南省巍山县等地700多户农户抽样调查，得出短期科技减贫作用明显的结论［7］。还有一些学者以效率测算为导向，尝试精确量化科技减贫效果。如Havibov等利用数据包络分析（DEA）方法，选取福利、税收、补贴等间接代理指标作为投入变量，贫困发生率作为产出变量，考察减贫投入的效率问题［8］。陈薇等用DEA方法中的CCR模型，对河北省减贫资金的规模有效性与配置有效性进行评价［9］。陈诗一和张军运用DEA-Tobit两步法对政府财政支农资金效率进行了测算［10］。叶初升等采用了DEA理论与方法对减贫专项资金的绩效进行评价［11］。

综上所述，现有文献在农业科技减贫效率的相关研究上取得了一定的成果，但存在几个值得改进的方面：首先，由于学者们研究的时限、方法以及样本的不同，所得结论并不一致值得考究；其次，既有的成果大多数是单一应用传统的DEA 或SFA模型来考察农业科技减贫效率，忽略了环境因素以及包含在冗余变量中的其他因素对效率水平的影响，这在一定程度上导致研究结论缺乏准确性；最后，专门针对湖南县域农业科技减贫效率进行系统分析的文献目前还较少见。鉴于以上原因，本文运用DEA与SFA相结合的三阶段DEA模型，以2012年湖南20个国家级贫困县域数据为样本对区域减贫效率值进行测度，分类并分析影响因素，以期更为系统全面、真实准确地考察农业科技减贫效率，并在此基础上提出效率优化的路径和方向。

二、研究方法与数据说明

（一）三阶段模型

传统DEA模型由Charnes、Cooper和Rhodes 于1978年提出的一种非参数估计方法［12］，因其无须设定固定函数关系而被研究者广泛采用，成为测度效率的经典模型。随后一些学者不断完善，Fried等提出DEA与Tobit相结合的两阶段方法（有文献称为四阶段法）［13］，来同步分析效率以及影响效率的因素。Simar和Wilson发现普通的两阶段分离计量方法会产生估计偏误，进而提出利用Bootstrap DEA两阶段模型来获得无偏估计量［14］。然而传统DEA模型与两阶段DEA的共同问题在于，测度出的效率值包含了环境变量与随机项等因素的影响。因此Fried等在此基础上又进一步提出了DEA与SFA相结合的三阶段DEA模型［15］，利用SFA对管理无效率、环境因素和随机误差等进行剥离，使得所计算出来的效率值更为真实、准确地反映DMU（Decision Making Unit，决策单元）效率。

1.第一阶段：采用传统DEA方法测算效率。假定规模报酬可变（VRS，Variable Returns Scale），采用以投入为导向的BCC模型，考察基于原始投入与原始产出数据的各决策单元的效率。与CCR模型（假定规模报酬不变）相比，BCC模型可以对非最佳生产规模和技术上的无效率分解，并将技术效率进一步分解为规模效率和纯技术效率，从而更好地反映决策单元的管理水平。假设DMU个数为n，投入变量个数为m，产出变量个数为s，Tk表示第k个决策单元的技术效率，yrk表示第k个决策单元的第r个产出变量，xik表示第k个决策单元的第i个投入变量，λr和θi分别表示第r个产出变量与第i个投入变量的权重系数，μk表示第k个决策单元的规模报酬指标。投入导向的BCC-DEA模型可以表示为：

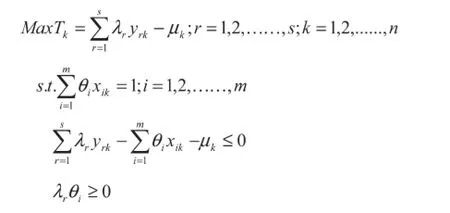
变量μk是区分BCC-DEA模型与CCR-DEA模型的指标，其结果显示了DMU的规模报酬状态。μk＞0，表示该决策单元处于规模报酬递减状态；μk=0，表示该决策单元处于规模报酬不变状态；μk＜0，表示该决策单元处于规模报酬递增状态。

2.第二阶段：运用SFA模型分解第一阶段的松弛变量，这是三阶段DEA方法的关键。Fried等认为，第一阶段分析得出的投入、产出松弛变量受环境因素、随机因素和管理效率三部分的影响［15］。但传统DEA模型并未将这三部分因素对效率值的影响进行区分，由此计算出的效率值不能反映到底是管理原因造成的低效，还是环境因素或随机干扰所导致的低效。第二阶段的目的就是把第一阶段的松弛量分解为这三部分，进而剔除环境因素和随机因素，得出仅由管理无效率造成的DMU投入冗余。首先定义第一阶段产生的投入松弛变量如下式：

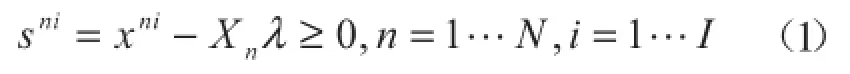
xni为第一阶段第i个生产者的第n种投入，Xn为X的第n列，Xnλ为第i个DMU的第n种投入值在效率前沿面的最优映射。投入松弛量包括径向与非径向两部分。再假定有K个可观测的环境变量，构建SFA回归方程如下：

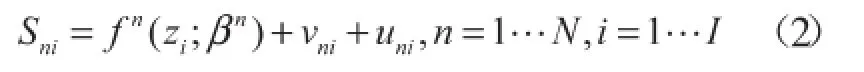
采用最大似然法估计得出未知参数，再对原始投入变量作如下调整：

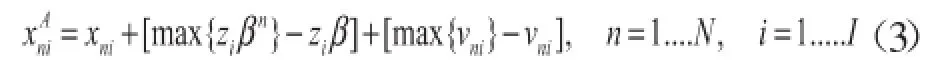
在此式中和xni分别代表调整后和调整前投入数量。式（3）右边第一调整项使所有生产者在同一生产环境中生产，即观察样本中最不利环境。第二调整项使所有生产者遇到最坏的运气。具有相对不利生产环境和相对坏运的生产者把投入向上调整相对较少的数量，而具有相对有利生产环境和相对好运的生产者把投入向上调整相对较多的数量。

为了计算式（3），必须把式（2）中的统计噪音与管理非效率进行分离，这样才能得到每个生产者统计噪音估计值。借鉴Jondrow给出的方法进行计算［16］：

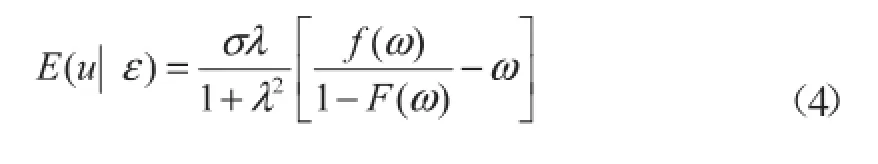
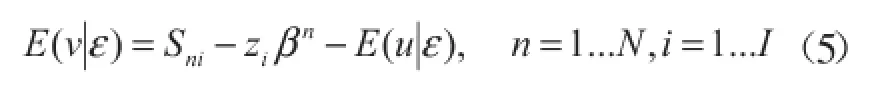
最后再将结果代入（3）式，便得出了调整后的投入变量值。

3.第三阶段：利用二阶段计算出的调整后投入变量值与原始产出值，再次进行DEA测算，由此得到的各个决策单元的效率值即为剔除了环境因素、随机误差影响的效率值。

（二）投入产出指标、环境变量的选取及数据来源

1.指标选取。投入指标应选取决定减贫的内生变量，根据经济基本理论的假定，拟选取人、财、物三大基本要素作为投入指标，考虑到数据可得性，分别用农业科技人员数、农业科技支出额，农业科研机构固定资产投资额表示。产出方面选取农村地区人均收入为产出变量，以保证与投入变量的统计口径保持一致，代表农村地区贫困指标。环境变量应选取对农村地区人均收入产生影响但不在样本主观可控范围的外生变量。本文拟选取宏观经济环境、政府政策支持、金融发展水平、信息化水平、教育水平、医疗卫生条件以及自然灾害七个指标作为影响减贫效率的环境因素。各变量的定义与度量如表1所示。

2.数据来源与研究对象说明。以上所有投入产出数据与环境变量数据，均根据《中国统计年鉴》与《中国县域统计年鉴》以及《中国科技年鉴》整理测算而得。截至2014年12月，根据国家扶贫规划确定的国家级贫困县的最新名单，湖南共有国家级贫困县20个。本文以这20个县域作为研究样本。

三、实证结果分析

（一）第一阶段：基于原始投入和产出数据的BCC模型估计

首先利用原始的投入变量数据，采用DEAP2.1软件对湖南省88个县域的农业科技减贫效率水平进行分析，计算结果如表2所示。

表3的结果显示，在未分离环境变量和随机因素影响的情况下，2012年湖南各县域农业科技减贫效率平均值为0.57，纯技术效率均值为0.66，规模效率均值为0.85。这表明湖南县域农业科技减贫效率偏低，且主要原因是资源配置不合理，而非投入规模不足。20个县之间的效率存在较大差异，其中邵阳县三项效率值均为1，处于效率前沿面；另外邵阳、新化、桑植、沅陵四县规模效率值为1，说明该四县在现有的生产可能性曲线上，其投入资源规模是有效率的；减贫效率在0.7以上的只有4个县，而低于0.5以下的县有7个。由于该测试结果还包含了环境因素和随机因素的干扰，并不能反映各县域的农业科技减贫效率的真实水平，为得到更为真实合理的结果，还需作更进一步地调整和测算。

（二）第二阶段：利用SFA模型分析环境变量、调整投入变量

以第一阶段deap计算结果里面决策单元slack movement和radial movement两个数值的和，作为投入松弛变量（即投入冗余），定义为第二阶段的被解释变量，以前文拟定的7个环境变量作为解释变量，利用Frontier4.1软件包，采用极大似然估计法（MLE，maximum likehood estimate）计算各环境变量对三个投入变量冗余的影响，得出的SFA回归结果见表3。

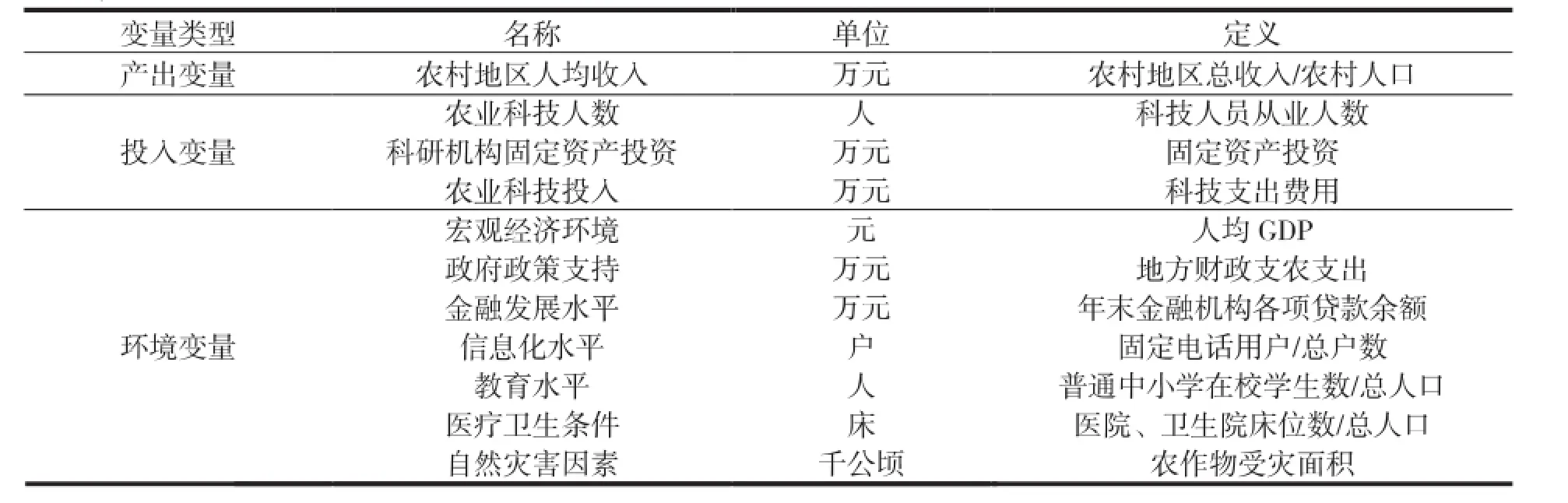
表1　变量的定义与度量

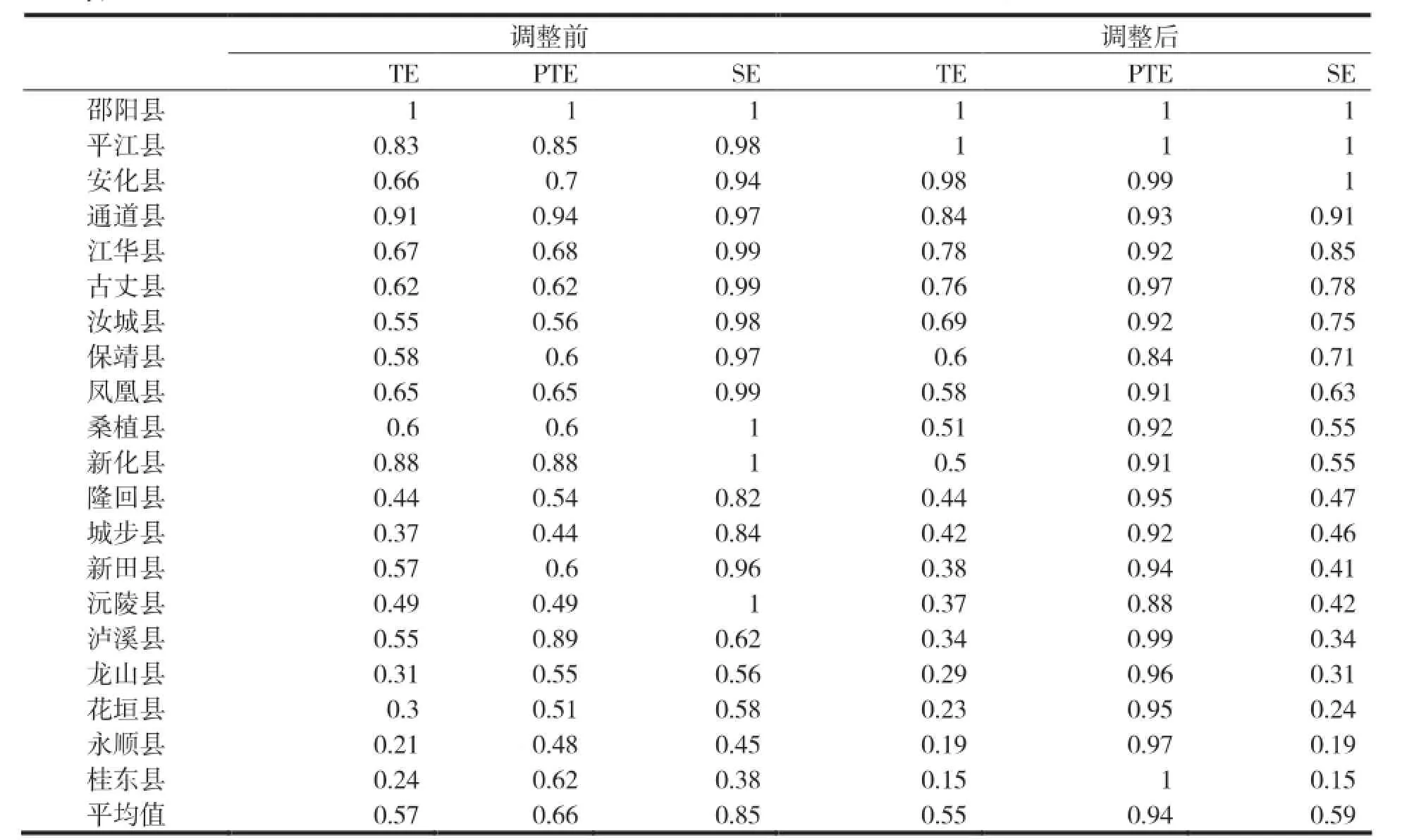
表2　第一阶段和第三阶段湖南88个县农业科技减贫效率值

对各系数项做进一步分析，若相关估计系数为正，表示环境变量的增大将导致投入冗余变量的增加，导致成本增加或产出降低；相反若估计系数为负，则表示环境变量的增大有利于投入冗余变量的减少，即有利于咸少投入变量的浪费或增加产出。具体而言：宏观经济环境、教育、医疗、信息化几项指标的影响系数均为负，并且均能通过10%的显著性检验。也就是说这些外部环境较好时，投入的松弛量将会减少，从而对农业科技减贫效率产生有利的影响。

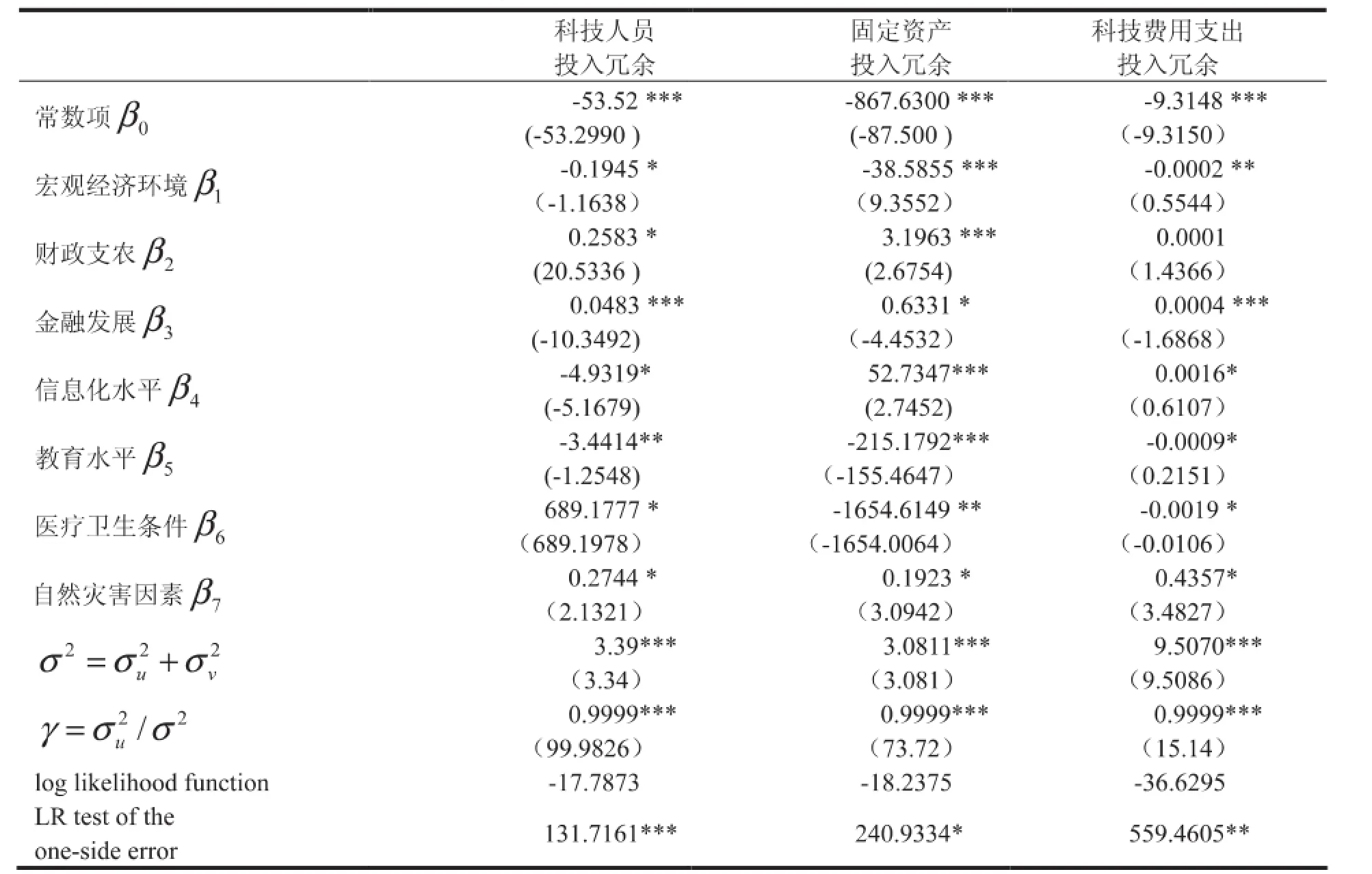
表3　环境变量对投入冗余变量的回归估计结果

结果表明，主要的环境变量对3种投入松弛变量的系数均通过显著性检验，且3个模型的LR单边检验中有两个达到了1%的显著性水平，另两个也分别在5%和10%水平通过了检验。这说明外部环境因素对湖南省各县的农业生产投入冗余存在显著影响，证明了环境变量选取的合理性。同时，4个回归模型的值（技术无效率方差占总方差的比重）均达到了0.99，并在1%置信水平显著。这表明影响4种投入冗余的因素中，随机误差影响占据主导地位。这一结果表明管理因素和随机因素对农业科技减贫效率存在着显著的影响，应用SFA进行管理因素和随机因素对效率影响的剥离分析是很有必要的。

政府政策支持力度和农村金融发展水平系数为正，说明这两项指标的提高对减贫效率不利。这可能是财政和金融资源的分配，当前并未能公平流入贫困人群，反而加剧了贫富差距问题。另一个可能的原因是由于政府惠农政策反而提高了农户的收入预期而盲目扩大生产，导致农业粗放型经营模式更趋恶化。

由以上分析可知，环境因素对湖南各县的投入冗余变量具有显著影响，且其影响方向与影响程度各有差异，如果不剥离环境因素，其计算出来的结果并不能真实客观地反映各县效率值。因为处于“较好”环境条件下的县域样本效率自然就会更高，而处于“较差”环境的样本公司效率就会被低估。因此，必须结合第二阶段的分析结果，调整原始投入数据，使得湖南省20个县域处于同质的环境条件和同样的随机条件下，再考察各县的真实减贫效率水平。

（三）第三阶段：对投入调整后的减贫效率再估计

运用上文给出的方法与上阶段的计算结果，根据式（3）调整投入变量，并将调整后的投入值与原始产出再次代入BCC模型进行分析，计算第三阶段各决策单元的效率值，为了便于对比分析，本文将第一阶段的效率值和第三阶段的效率值同时放入表2中，由表2结果可知：

剔除环境变量和随机因素的影响后，各县域减贫效率值发生了较明显的变化。农业科技减贫效率平均值、纯技术效率均值以及规模效率均值分别由原来的0.57、0.66、0.85变为0.55、0.94、0.59。这跟原来的结论有很大不同，即调整后的减贫效率稍有降低，造成湖南省各县域农业科技减贫效率低下的主要原因是规模效率低下。各县域农业的纯技术效率值有较明显增高，说明第一阶段纯技术效率低下主要是由“较差”的环境条件或“较大”的随机误差导致的。另外各个县域之间的差距较大，综合技术效率值大于0.7的有6个县，低于0.5的有9个县，差距进一步拉大。具体而言：

综合减贫效率排名发生了变化，邵阳、平江以及安化处在前三位，表明这几个县域在剥离环境因素和随机干扰后的同质环境下科技减贫依然是高效的。而新田、沅陵、泸溪三县的名次下降幅度较大，这说明他们之前的高效率与他们所处的有利环境密切相关。特别的，排名靠后的县域如龙山、花垣、永顺、桂东四县中，名次变化不大，且规模效率依然偏低，说明对这几个县而言，环境因素等外部变量并不是其落后的原因，内在因素才是决定其落后的根源。或者说，农业科技投入要达到一定规模之后，这些环境因素的影响才能体现。

四、结论及政策启示

（一）结论

本文运用DEA与SFA相结合的三阶段DEA模型，对剔除环境因素和随机误差影响前后的湖南20个国家级贫困县的农业科技减贫效率进行再评估，得出如下结论：第一，湖南县域农业科技减贫效率受环境因素的影响较大。其中政府财政支农投入与金融资源的非平等性分配，不利于农业科技减贫效率的改进；而经济发展、教育、医疗以及信息等资源与服务在农村的普及和发展能够有效地促进减贫效率。第二，剔除环境因素与随机误差的影响后，绝大多数县域的综合减贫效率和规模效率呈现下降的趋势，而纯技术效率普遍上升。说明对绝大部分县域而言，调整前纯技术效率低下主要是由“较差”的环境条件或“较差”的运气所致，并非实际管理水平较差，且农业科技减贫效率低下的主要原因是源自规模效率低下及投入不足。而县域间的农业科技减贫效率差异较大，且规模效率的差距要较纯技术效率的差距大得多。

（二）政策启示

根据上述结论，本文得出以下几点政策启示：第一，针对湖南省农业科技投入不足的问题，应发挥政府之外的市场力量，吸收和引导外部资金如企业进行科技投入，不能单单依赖政府，促进贫困县域农业科技形成规模产生集聚效应。第二，政府方面应创新财政支农方式，切实保证财政支农资金落到实处。第三，重视金融资源的扶贫作用，尤其应创造公平环境，避免金融资源被富裕阶层垄断无法流入贫困人群。第四，继续加大人力资本投入，切实改善农村的教育医疗环境，强化公共服务供给体系。第五，实施区域差异化发展战略，缩小各县域科技减贫环境差距，推动相对落后地区科技减贫效应充分发挥。

［1］Mills，Bradford F.Ex Ante Research Evaluation and Regional Trade Flows：Maize in Kenya［J］.Journal of Agricultural Economics，1998，49（3）：393-408.

［2］Kersting，Wolfgang Source Der

Kosovo-Krieg und das V？lkerrecht/hrsg. vonReinhardMerkelPublisherFrankfurtamMain：Suhrkamp，2000：187-231.

［3］Reddy，Balwanth.endogenous wage rate，choice of technique and abelian&optimaal trajectories［J］.Metroeconomica，1972，24（2）：167-179.

［4］Gunasena H P M，Gunasena hpm.food and poverty：technologies forpoverty alleviation［J］.South Asia，2003，12 （2）：76-93.

［5］Keijiro Otsuka.Role of agriculturalresearch in poverty reduction：lessons from the Asian experience［J］.Food Policy，2000，（25）：447-462.

［6］陈来生，马晓岗，马进福.农业科技扶贫技术项目选择及效率评价［J］.安徽农业科学，2007，（35）80-81.

［7］汪三贵，李文，李芸.我国扶贫资金投向及效果分析［J］.农业技术经济，2004，（5）：45-49.

［8］Havibov N N，Lida F.Comparing and contrasting poverty reduction performance of social welfare programs across juris-dictions in Cannada using Data Envelopment Analysis（DEA）：an exploratory study of the era of devolution ［J］.Evaluation and Program Planning，2009，33（4）：457-467.

［9］陈薇.河北省财政扶贫政策绩效评价实证研究［J］.农业经济，2006，（07）：58-59.

［10］陈诗一，张军.中国地方政府财政支出效率研究：1978-2005［J］.中国社会科学，2008，（04）：65-78，206.

［11］叶初升，邹欣.扶贫瞄准的绩效评估与机制设计［J］.华中农业大学学报（社会科学版），2012，（01）：63-69.

［12］Charnes A，Cooper W W，Rhodes E.Measuring the efficiency of decision making units［J］.European Journal of Operational Research，1978，6（2）：429-444.

［13］Fried，H.O.，S.Schmidt，et al.Incorporating the Operating Envirronment into a Nonparametric Measure of TechnicalEfficiencyJournalofproductivityAnalysis. 1999，12（3）：249-267.

［14］Sima，L，P.W.Wilson.Estimation and Inference in Two-Stage，Semi-Parametric Models of Productiong Processes［J］.Journal of Econometrics，2007，136（1）：31-64.

［15］Fried，Lovell，Schmidt and Yaisawarng，2002，Accounting for Environmental Effects and Statistical Noise in Data Envelopment Analysis［J］，Journal of Productivity Analysis，17，121-136.

［16］Jondrow，J.，I.Materov，C.A.K.Lovell and P.Schmidt. On the Estimation of Technical Inefficiency in the Stochastic Frontier Production Model［J］.Journalof Econometrics，1982，（19）：233-238.

（责任编辑：胡宜挺）

湖南省社科基金资助项目（15YBA327）；湖南省教育厅基金资助项目（2015C1218）；衡阳市社会科学基金资助项目（2015C001）。

陈鸣（1977-），男，湖南常德人，湖南农业大学博士研究生，南华大学经济管理学院讲师，研究方向：农业经济管理。