斜拉桥双边箱主梁剪力滞效应分析

赵现省，陈雄飞

斜拉桥双边箱主梁剪力滞效应分析

赵现省，陈雄飞

（江苏扬子大桥股份有限公司， 江苏 江阴 214521）

斜拉桥主梁截面一般采取双边箱结构形式，截面一般较宽，存在着明显的剪力滞效应。文章分析了斜拉桥在最大悬臂施工阶段和成桥阶段主梁剪力滞效应的影响，通过在主梁增加纵向加劲肋减小了斜拉桥的剪力滞效应，改善了桥面的受力，可为斜拉桥的设计及施工提供参考。

斜拉桥；施工阶段；成桥阶段；纵向加劲肋；剪力滞

斜拉桥主梁截面一般较宽，宽箱形截面主梁在自重和荷载作用下挠曲时，由于腹板传递的剪力流在边缘上受力要大一些，而向板内传递过程中，由于上下板均会发生剪切变形，应力会逐渐减小，故实际上板的应力在截面分布是不均匀的，这个现象就称为剪力滞效应［1］。当靠近肋板处的主梁正应力大于远离肋板处主梁的正应力时，称为正剪力滞；当靠近肋板处的主梁正应力小于远离肋板处主梁的正应力时，称为负剪力滞［2］，如图1、图2所示（图中虚线所示为按初等梁理论计算得到的正应力值）。

1　工程概况

本文研究的对象是一座预应力混凝土斜拉桥，该桥主桥跨径为（152+370+152） m，采用双塔双索面，全漂浮体系。主梁为双边箱梁，主梁中心高3.2 m，宽38.6 m，桥面板厚0.3 m。索塔成H形，高137 m，预应力混凝土结构。斜拉索采用OVM250系列环氧涂层钢铰线拉索及相应的锚具，标准强度为1 860 MPa，弹性模量为1.95×105MPa。斜拉索一共124对，斜拉索一端为张拉端锚具，另一端为锚固端锚具，斜拉索在主梁上的标准索距为6 m。该桥主桥布置及主梁典型断面分别如图3、图4所示。

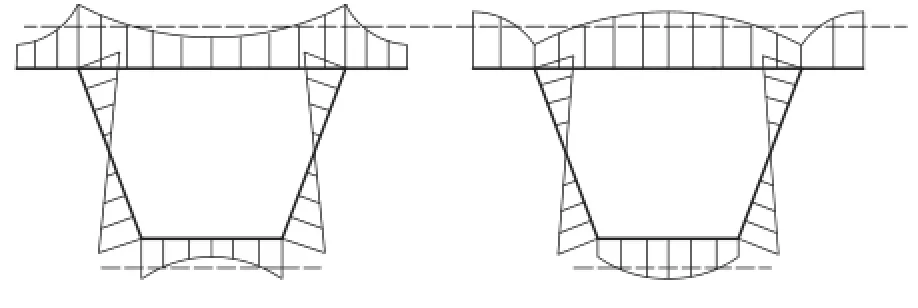
图1　正剪力滞效应 图2 负剪力滞效应

2　斜拉桥双边箱主梁剪力滞效应分析［3-5］

本文采用大型综合有限元分析软件ANSYS建立有限元模型，单元采用人工划分。斜拉索采用空间杆单元LINK8模拟，主梁采用实体单元SOLID45模拟。在悬臂施工阶段，主梁和索塔是固结的，故主梁和拉索的边界采用全约束；在成桥阶段，主梁约束条件为纵横向约束，转动约束，竖向无约束。

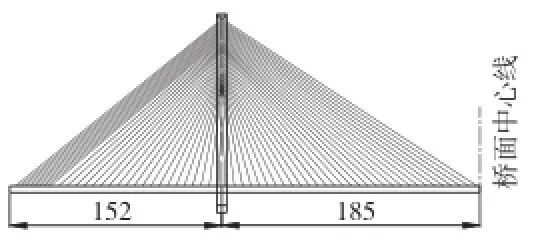
图3　主桥布置图（单位：m）

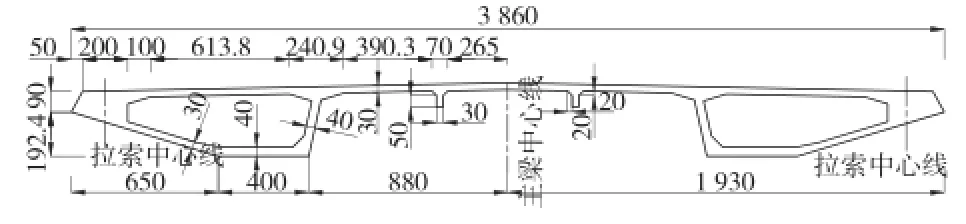
图4　主梁典型断面图（单位：cm）

2.1最大悬臂施工阶段

（1）有限元计算应力值

在纵向选取桥梁最大悬臂跨径的1/4、1/2、3/4截面，在横向选取有代表性的点进行分析，横向点的位置如图5所示：

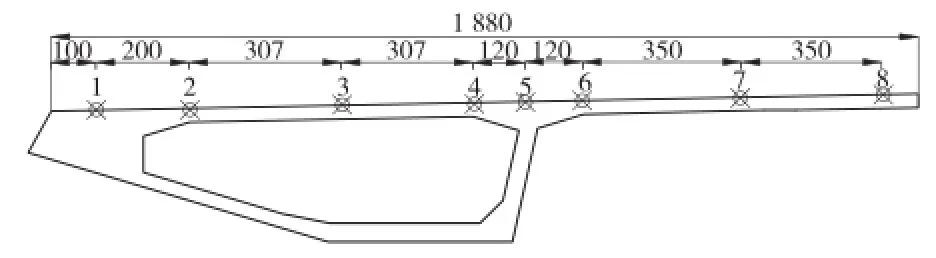
图5　横向计算点布置图（单位：cm）

计算结果如表1所示，其中正值代表拉应力，负值代表压应力。

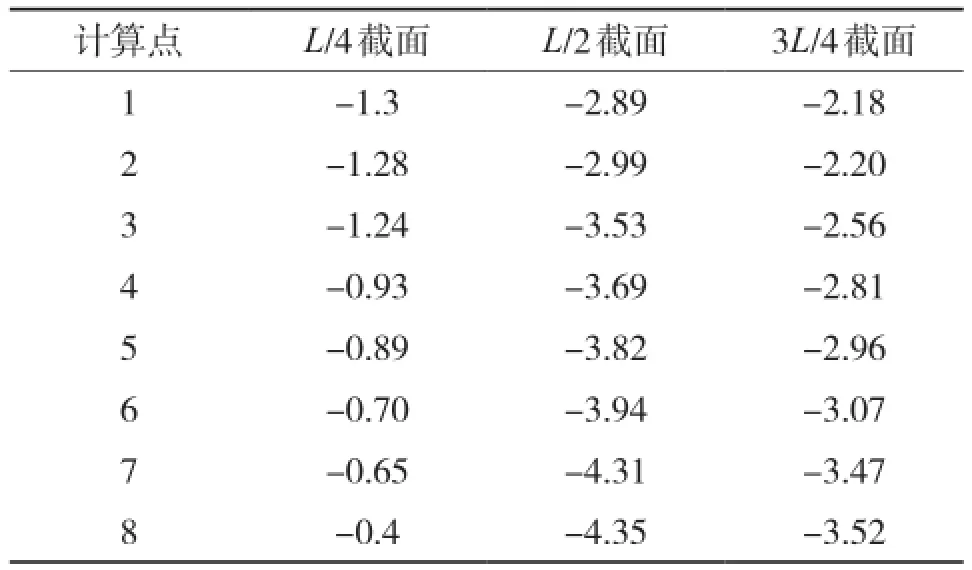
表1　自重作用下箱梁截面应力值 MPa

由表1可以看出：在L/4截面，截面应力由主梁边缘向跨中逐渐减小；在L/2截面、3L/4截面，截面应力由主梁边缘向跨中逐渐增大。

（2）初等梁理论计算应力值

根据初等梁理论，可以计算出主梁1/4、1/2、3/4截面的平均应力，该应力由弯曲应力和轴向压应力两部分组成，可由式（1）计算：

因此可以得到斜拉桥在双悬臂状态时主梁截面的平均应力如表2所示：

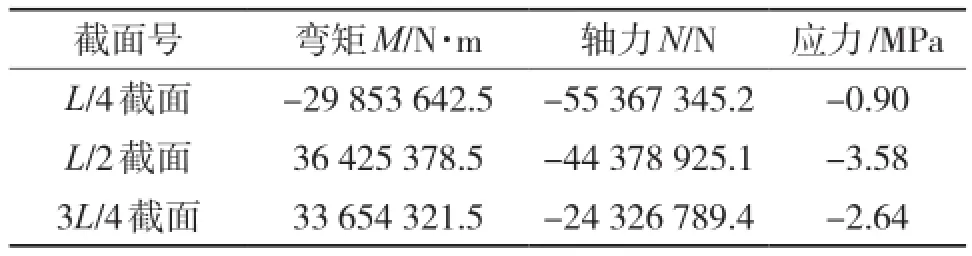
表2　自重作用下箱梁截面平均值

（3）最大悬臂状态下箱梁剪力滞系数

根据考虑剪力滞影响的有限元计算出的应力值除以初等梁理论状态下计算出来的平均应力值，就可以得到箱梁剪力滞系数：

计算结果如表3所示：

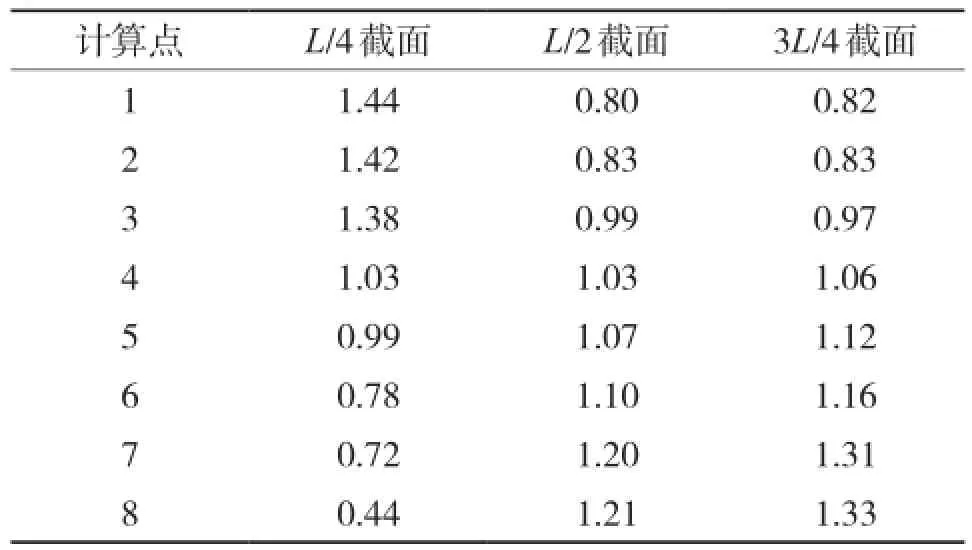
表3　最大悬臂状态下箱梁剪力滞系数

由表3可以看出，主梁在同一截面不同计算点的剪力滞系数不同。在L/4截面，主梁的剪力滞系数由边缘向跨中逐渐减小，在L/2截面和3L/4截面，主梁的剪力滞系数由边缘向跨中逐渐增大；L/4截面主梁呈现明显的正剪力滞效应，而L/2截面和3L/4截面主梁呈现明显的负剪力滞现象。

2.2成桥阶段

（1）有限元计算应力值

在纵向选取桥梁截面如图6所示，横向点的选取位置如图5所示。

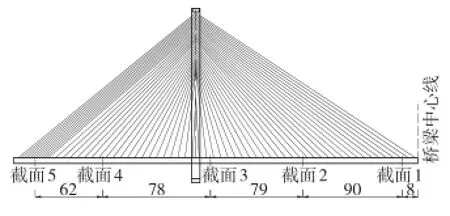
图6　成桥阶段纵向截面（单位：cm）

计算结果如表4所示（其中正值代表拉应力，负值代表压应力）。

（2）初等梁理论计算应力值

根据初等梁理论，可以计算出主梁截面1、2、3、4、5的平均应力，因此成桥阶段主梁截面的平均应力值如表5所示。

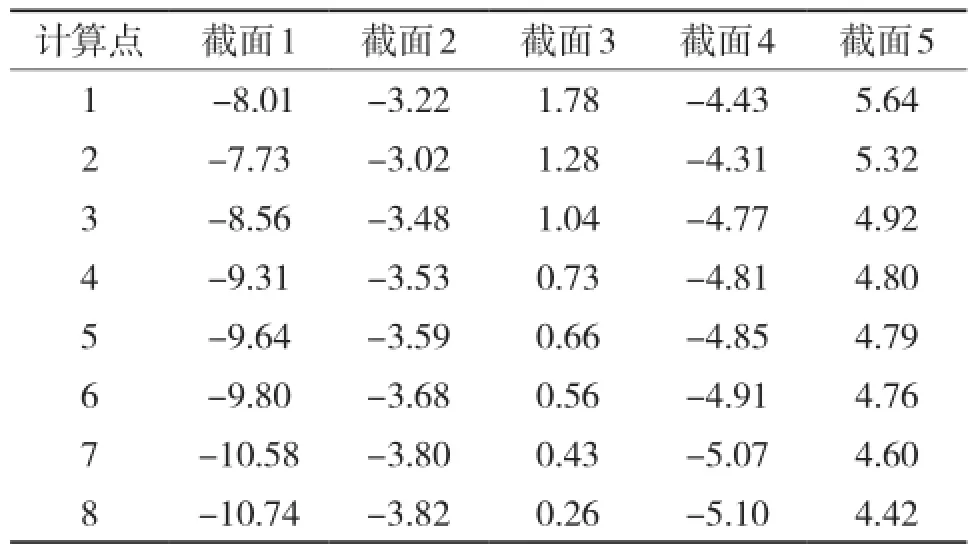
表4　成桥阶段箱梁截面应力值 MPa

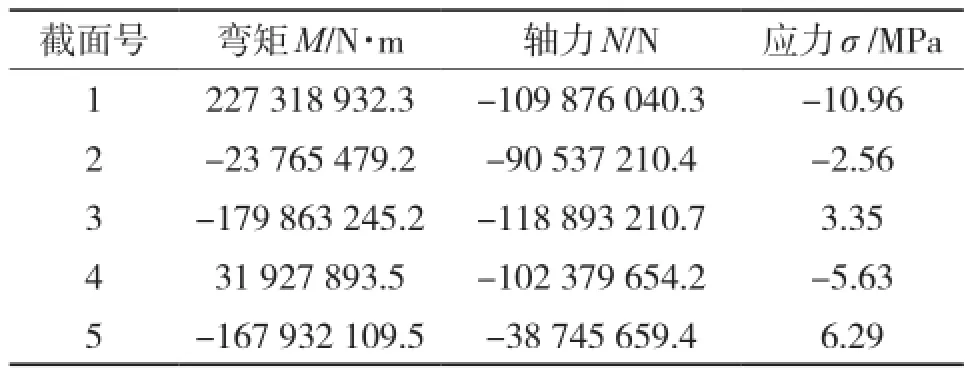
表5　成桥阶段箱梁截面平均应力值

（3）成桥阶段下箱梁剪力滞系数

成桥阶段箱梁剪力滞系数如表6所示：

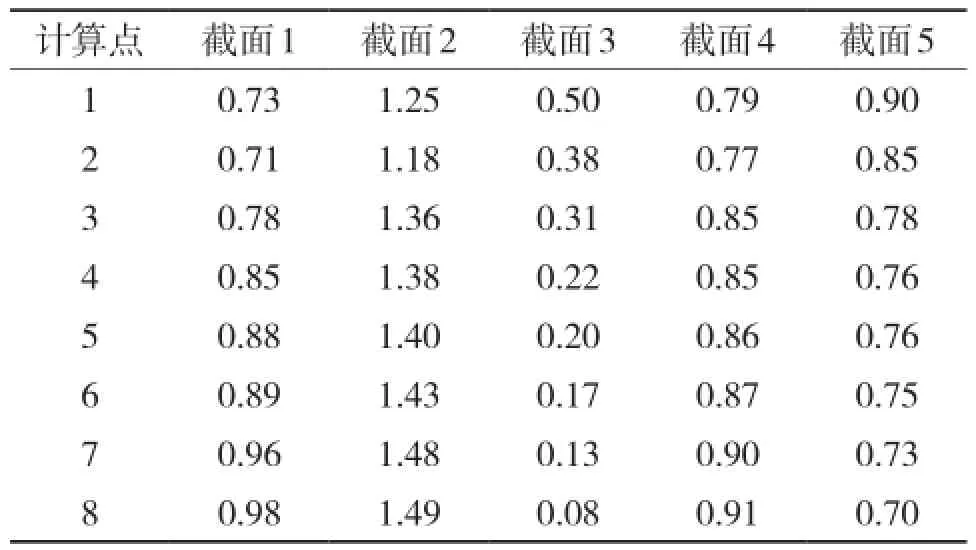
表6　成桥阶段箱梁剪力滞系数

由表6可以看出，主梁在同一截面不同计算点的剪力滞系数不同。

（1） 截面2主梁剪力滞系数大于1，而其他截面主梁剪力滞系数均小于1。各截面最大剪力滞系数为1.49，最小剪力滞系数为0.08；

（2）截面1、2、4剪力滞系数由边缘向跨中逐渐增大，截面3、5剪力滞系数由边缘向跨中逐渐减小；

（3）截面2主梁呈现负剪力滞效应，截面1、3、4、5主梁呈现明显的正剪力滞现象。

3　设置纵向加劲肋对双边箱主梁剪力滞效应的影响分析［6-10］

在不改变主梁外轮廓尺寸的条件下，可以在双边箱主梁之间增加纵向加劲肋来减小剪力滞效应带来的危害。该桥两双边箱主梁之间的净距离为14 m，在其中设置两道纵向加劲肋，间距为5.3 m，纵向加劲肋截面为矩形，如图4所示。

本节重新建立增加纵向加劲肋的空间有限元模型，所选工况为最大悬臂状态下，在纵向选取桥梁最大悬臂跨径的1/4、1/2、3/4截面，横向选取点的位置如图5所示，计算结果如表7所示（其中正值代表拉应力，负值代表压应力）。

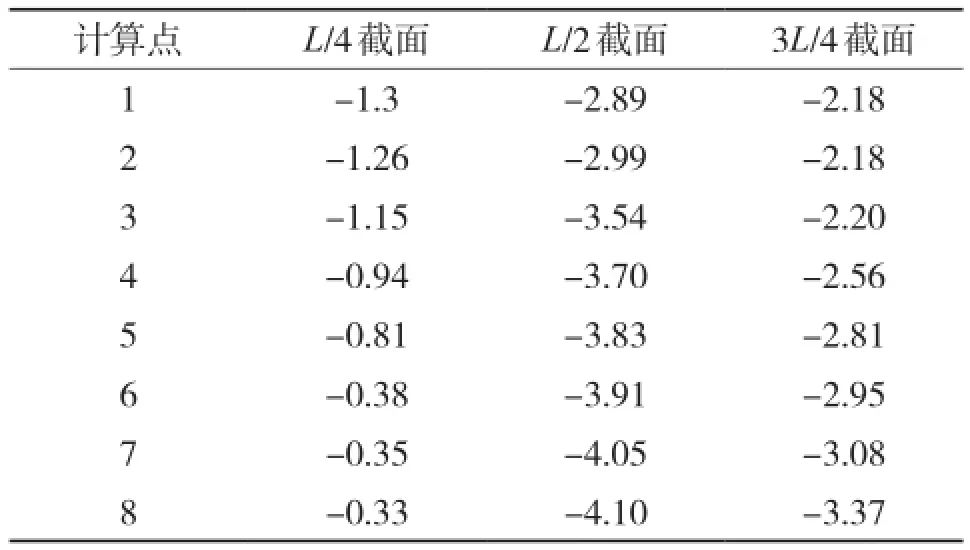
表7　设置加劲肋后自重作用下箱梁截面应力值 MPa

由表7可以看出：

（1）在L/4截面，主梁的截面应力由边缘向跨中逐渐减小，在L/2截面和3L/4截面，主梁的截面应力由边缘向跨中逐渐增大；

（2）将表7与表1进行对比，设置纵向加劲肋后，主梁截面应力有所减小，其中L/4截面应力最多减小了46%，L/2截面应力最多减小了6%，3L/4截面应力最多减小了11%；

（3）设置纵向加劲肋后并没有改变截面应力增大或者减小的趋势，但是纵向加劲肋使得各截面纵向正应力分布变得更加均匀。

根据初等梁理论，计算出增加加劲肋状态下主梁的1/4、1/2、3/4截面的平均应力，如表8所示：

将表8与表2进行对比可以看出，设置纵向加劲肋前后，按初等梁理论计算的截面正应力几乎没有改变。

则设置加劲肋后双边箱主梁的剪力滞系数如表9所示。由表9可以看出：

（1）在L/4截面，主梁的剪力滞系数由边缘向跨中逐渐减小，在L/2截面和3L/4截面，主梁的剪力滞系数由边缘向跨中逐渐增大；

（2）将表9与表3进行对比，设置纵向加劲肋后，主梁的剪力滞效应有所降低，其中主梁L/4截面处，设置加劲肋后，剪力滞系数最多减小了47%；主梁L/2截面和3L/4截面处剪力滞系数最多减小了4%。

（3）桥面板设置纵向加劲肋后，没有根本性改变主梁截面上的剪力滞系数的分布情况，但是纵向加劲肋使得主梁各截面剪力滞系数分布变的更加均匀。

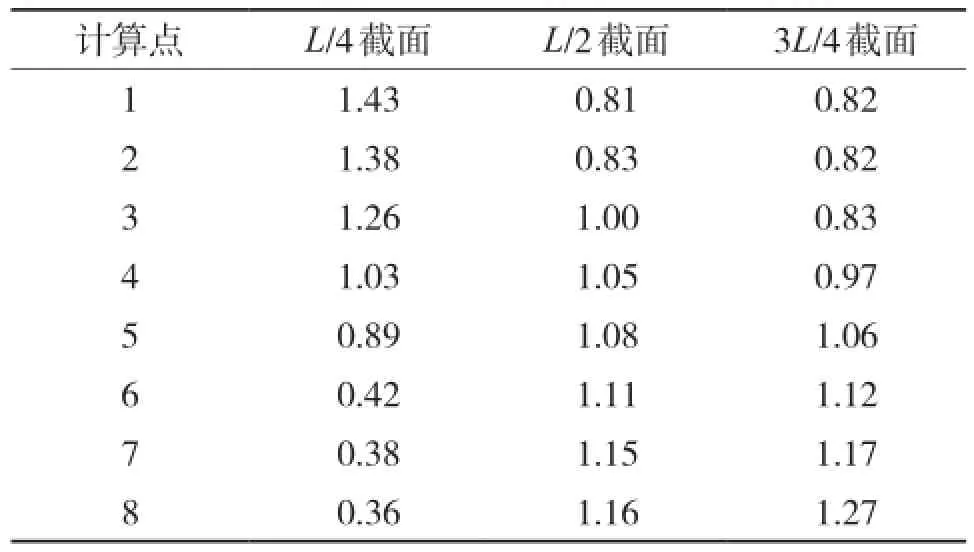
表9　设置加劲肋后箱梁剪力滞系数

4　结论

（1）未设置纵向加劲肋前，斜拉桥在最大悬臂施工阶段和成桥阶段，双边箱主梁的应力和剪力滞分布不均匀，但是成桥阶段的应力和剪力滞分布比施工阶段要均匀一些；

（2）设置纵向加劲肋后，双边箱主梁的应力和剪力滞效应得到了改善。其中， L/4截面应力最多减小了46%，L/2截面应力最多减小了6%，3L/4截面应力最多减小了11%；L/4截面剪力滞系数最多减小了47%，L/2截面和3L/4截面处剪力滞系数最多减小了4%；

（3）通过构造措施，即在桥面板纵向设置加劲肋，的确可以减小双边箱主梁的截面应力和剪力滞效应，从而改善桥面的受力，为双边箱主梁斜拉桥的施工和设计提供参考。

［1］高晶. 纵向加劲肋桥面板受力性能的模型试验研究［D］.南京：东南大学.2006.

［2］叶见曙. 结构设计原理第2版. ［M］.北京：人民交通出版社，2004.

［3］林元培. 斜拉桥［M］. 北京：人民交通出版社，1994.

［4］许崇法. 斜拉桥混凝土主梁桥面板模型试验与分析［D］.南京：东南大学.2004.

［5］韦成龙，曾庆元，刘小燕.薄壁曲线箱梁桥剪滞效应分析的一维有限单元法［J］.中国公路学报，2000，13（1）：65-68.

［6］周世军.箱梁的剪力滞效应分析［J］.工程力学，2008，25（2）：204-208.

［7］何初生.滨州黄河大桥主梁剪力滞的模型实验研究［D］.南京：东南大学.2004.

［8］兰鹏臻，周世军.基于剪切变形规律的箱梁剪力滞效应研究［J］.铁道学报，2011，33（4）：100-104.

［9］E Reissner. Analysis of shear lag in box beams by the principle of minimum potential energy［J］. Quart Appl Math ，1946，（4）：268-278.

［10］Shih Toh Chang. Prestress Influence on Shear-Lag Effect in Continuous Box-Girder Bridge［J］. Journal of Structural Engineering，1992，118（11）：3113-3121.

Shear Lag Effect Analysis of Bilateral Box Girder for Cable-stayed Bridge

Zhao Xiansheng，Chen Xiongfei
（Jiangsu Yangzi bridge Co.， LTD， Jiangyin 214521， China）

Bilateral box structure was generally adopted for cable-stayed bridge girder cross section. The cross section were usually wide with obvious shear lag effect. This paper analyzed the shear lag effect during the longest cantilever construction stage and finished stage for cable-stayed bridges. Shear lag effect decreased by setting longitudinal stiffener. It could be taken as reference for design and construction of cable-stayed bridges.

cable-stayed bridge； construction stage； finished stage； longitudinal stiffener； shear lag

U441.5

A

1672-9889（2015）06-0032-04

赵现省（1985-），男，河南濮阳人，硕士研究生，研究方向为高速公路公路桥梁养护。

（2015-03-26）