基于灰色关联法的拥堵费额度模型构建

戴仲娜

基于灰色关联法的拥堵费额度模型构建

戴仲娜

（南京理工大学自动化院，江苏 南京 210094）

文章利用灰度关联法，分析了影响拥堵费额度的主要因素并构建模型。研究表明，该方法可以从少量的现有数据中，同时研究收费额度与多个影响因素之间的关系，分辨这些因素影响程度大小，用SPSS软件拟合数据，建立拥堵费额度模型，可为欲收取拥堵费的城市提供参考。

拥堵费额度；灰色关联法；模型

1　概述

随着城市交通供需矛盾的日益突出，交通拥堵越来越成为影响城市面貌、降低社会效率、抑制城市快速发展的症结。

为了缓解交通拥堵，许多城市采取了一系列有效的措施。主要为提高交通供给能力、改善城市布局、大力发展公共交通这几种方法。提高交通供给能力具体体现为城市道路的大量建设，但受到城市用地的限制，当道路扩建到一定程度后，就不能继续扩建；改善城市布局也非一朝一夕可以实现，在城市规划中要注意各功能区域的合理安排，从需求上减少交通流；大力发展公共交通在近年来有很大成效，很多城市响应“公交优先”政策，大力发展城市轨道交通、快速公交、公共自行车等公共交通。

以上3种措施确实在一定程度上能缓解交通拥堵，但机动车拥有量的持续快速增长使之急需另辟蹊径。而新加坡早在20世纪70年代，就通过收取拥堵费来缓解交通拥堵。此外，拥堵费在英国伦敦、瑞典斯德哥尔摩、挪威奥斯陆和特隆赫姆、美国加州及纽约都有应用［1］。我国一些一线城市可能会借鉴国外经验在未来几年收取交通拥堵费。

交通拥堵费是指在交通拥挤时段对部分区域道路使用者收取的一定费用。其本质上是一种交通需求管理的经济手段，目的是利用价格机制来限制城市道路高峰期的车流密度，改变交通流在时间和空间上的分布，达到缓解城市交通拥挤的目的，提高整个城市交通的运营效率［2］。

拥堵费收多少是大家都关心的问题。目前，国内外对拥堵费的理论研究较多，但涉及拥堵费的额度的研究较少。较新的研究，如Hillel Bar-Gera等对自动网络设计和道路收费的交通平衡灵敏度的计算精度有一定研究［3］，Andre de Palma等人研究了交通拥挤定价方法和技术［4］， Wei（David）Fan和ZegeyeGurmu用遗传算法研究联合决策的拥挤定价和容量扩展［5］，Xiaolei Guo等研究帕累托改进的拥塞定价及多类用户退款［6］，黎明和邢丽霞等从经济学角度对拥堵费额度进行分析计算［7-8］。

拥堵费额度的确定受诸多因素的影响，拥挤程度、汽车数量、人均收入、民众态度等等。本文按一定原则选取几个主要的可量化因素，包括汽车保有量、人口、人均收入、人均拥有车辆数等，利用灰度关联法研究收费额度与这些因素之间的关系，建立模型，为规划部门决策提供参考。

2　模型构建

2.1灰度关联法及其适用性分析

1982年邓聚龙创立了灰色系统理论，该理论认为所有信息都清楚的系统是白色系统，而所有信息都不知道的系统是黑色系统，灰色系统是介于两者之间的只有部分信息明确的贫信息、不确定性系统［9］。

灰度关联法是一种常用的灰色系统分析方法，它可以对系统的动态变化形势进行定量分析。该方法是通过各相关因素建立参考数据列和若干比较数据列，对其进行量化，通过比较数据列曲线几何形状的相似程度来判断其联系是否紧密，曲线越接近则联系度越大。即计算出各因素的“关联度”，通过比较“关联度”的大小来确定关联程度的大小［10-11］。

2.2适用性分析

目前，只有国外少数城市有收拥堵费缓解交通拥堵的经验，其中有些城市也才开始实施，关于这方面的数据不全并难以获取。同时，影响拥堵费额度的因素有很多，很难确定各个影响因素与收费额度的关联程度大小。而灰色关联法非常适用于这种“数据少”、“因素多”的问题，因此本文选择运用灰关联分析法确定拥堵费额度与各影响因素之间的关联程度，进而确定主要影响因素［12］。

2.3具体计算步骤

（1）定义序列

利用各城市收费额度和各个影响因素的数据形成参考数列和对比数列。

设Xi为系统因素，其在序号k上的观测数据为xi（k），k =1，2，…，n，可得行为序列Xi=（xi（1），xi（2），…，xi（n）），i=0，1，…，m，可以设X0为系统特征序列，表示拥堵费额度； X1，X2，…，Xn为影响因素序列，k为序号。

（2）无量纲处理

由于系统中各因素的物理意义不同，导致数据的量纲也不一定相同，不便于计算比较，或在比较时难以得到正确的结论。因此在进行灰色关联度分析时，一般都要进行无量纲化的数据处理，也称标准化处理。得到：

其中，xi（1）≠0；k =1，2，…，n；i=0，1，…，m。

无量纲处理后得到初始化数列为：

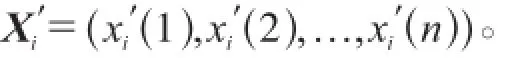
（3）求差序列

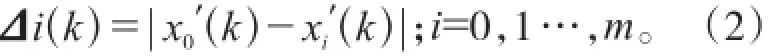
（4）计算最大差与最小差

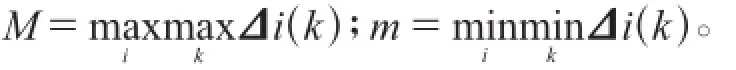
（5）求灰色关联系数

所谓关联程度，实质上是曲线间几何形状的差别程度。因此曲线间差值大小，可作为关联程度的衡量尺度。对于一个参考数列X0有若干个比较数列X1，X2，…，Xn，各比较数列与参考数列在各个时刻（即曲线中的各点）的关联系数可由公式（3）得出。

其中，ρ为分辨系数，一般在0～1之间，ρ的取值规则如下：

记v为所有差绝对值的均值，即：

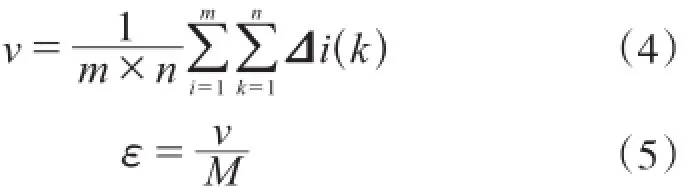
则ρ的取值为ε≤ρ≤2ε，且满足

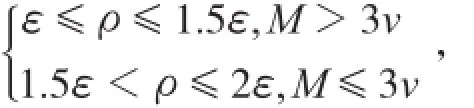
为了方便，通常可直接取ρ为0.5。

（6）求关联度ri

因为关联系数是比较数列与参考数列在各个时刻（即曲线中的各点）的关联程度值，所以它的数不止一个，而信息过于分散不便于进行整体性比较。因此有必要将各个时刻（即曲线中的各点）的关联系数集中为一个值，即求其平均值，作为比较数列与参考数列间关联程度的数量表示，关联度ri的计算如下：

其中，k =1，2，…，n；i=0，1，…，m。ri为比较数列Xi对参考数列X0的灰关联度，或称为序列关联度、平均关联度、线关联度。ri值越接近1，说明相关性越好。

（7）关联度排序

因素间的关联程度，主要是用关联度的大小次序描述，而不仅是关联度的大小。将m个子序列对同一母序列的关联度按大小顺序排列起来，便组成了关联序，反映了对于母序列来说各子序列的“优劣”关系。

（8）建立拥堵费额度预测模型

通过上述灰度关联法确定了各相关因素的影响程度大小后，需要建立以某个相关因素（比如车辆数）为自变量与拥堵费额度之间的函数关系式［13］，根据数据的特点选择合适的函数形式（如线性函数、复合函数等）。本文使用SPSS对各分组数据进行非线性回归分析［14］，再根据拟合程度选择最合适的拥堵费额度模型。

3　案例分析

S市想要通过收拥堵费来缓解交通拥堵，对已经收取拥堵费的城市A、B、C、D进行调研。按整体性原则、科学性原则、客观性原则、可操作性原则和可比性原则从众多影响因素中选取车辆数、人口数等6个因素作为影响收费额度主要因素，以期从得到的少量数据中知道收费额度与调研的哪个因素最为密切。调研数据如表1所示。

表1　拥堵费和各影响因素数据

设X0为系统特征序列，表示拥堵费额度；X1，X2，…，X6为影响因素序列，分别表示各类影响因素，k为城市序号，采用不同城市数据构成行为横向序列：Xi=（xi（1），xi（2），xi（3），xi（4）），i=0，1，…，6，由式

可得：

由式（2）可得

最大差与最小差分别为

由式（4）、式（5）得

因为M＞3v，所以ε≤ρ≤1.5ε，即（0.181 8，0.272 7）取ρ=0.2代入式（3）可得：

由式（6）可得拥堵费额度与6类影响因素的灰色关联度如表2所示。

4　结语

表2　拥堵费额度与6类影响因素的灰色关联度表

将灰色关联度按大小排列，得出结论如下：人均车辆数与车辆数是其中最关键的两个因素，人均收入与人口数次之，每平方公里车辆数与人口密度的灰色关联度最低，对拥堵费额度影响较小。这个结论与主观判断较为一致，说明用灰度关联法来研究拥堵费额度的影响因素有较高的可靠性。

根据数据分布特点选择适宜函数形式利用SPSS对各组数据进行拟合，文中只对人均车辆数和拥堵费额度之间的关系进行拟合，如图1所示，其余数据不一一举例。

拟合方程为Iny=-1.296+6.587x，R2=0.836。其中，y为拥堵费额度；x为人均车辆数。

（1）本文以国外已收取拥堵费城市的数据为例，使用灰关联分析法确定拥堵费额度与其几个影响因素之间的关联程度大小，再使用SPSS对交通调查数据进行非线性回归分析，进而得到拟合方程，最终得到各影响因素与拥堵费额度的函数模型。

图1　人均车辆数和拥堵费额度关系图

（2）通过更多调查数据验证，基本符合本文建立的模型，因此证明了模型的实用性，可以为规划部门决策提供一定的参考。我国城市收取拥堵费后，用国内城市的数据进行分析计算能得到更适应国内城市的函数模型。

（3）拥堵费额度有很多影响因素，非常复杂，灰度关联法能同时对比几个影响因素。除了文中案例分析的6个影响因素外，还可将民众态度、环境、能源、拥堵情况等因素量化后，用灰度关联法加以计算分析，构建更加精确的函数模型。

［1］吴艳.关于征收道路拥堵费的思考［J］.产业与科技论坛，2011，10（17）：60-61.

［2］单丽曼.关于北京市征收交通拥堵费的可行性研究［J］. 现代商业，2012（2）：131-131.

［3］Bar-Gera H， Hellman F， Patriksson M. Computational precision of traffic equilibria sensitivities in automatic network design and road pricing［J］. Transportation Research Part B：Methodological，2013（57）：485-500.

［4］de Palma A，Lindsey R. Traffic congestion pricing methodologies and technologies［J］. Transportation Research Part C：Emerging Technologies，2011，19（6）：1377-1399.

［5］Fan W，Gurmu Z. Combined Decision Making of Congestion Pricing and Capacity Expansion: Genetic Algorithm Approach［J］. Journal of Transportation Engineering，2014，140（8）.

［6］Guo X，Yang H. Pareto-improving congestion pricing and revenue refunding with multiple user classes［J］. Transportation Research Part B：Methodological，2010，44（8）：972-982.

［7］黎明.城市主干道交通拥挤收费额度的经济学计算［J］. 科技创业月刊，2009 （7）：89-90.

［8］ 邢丽霞.城市道路拥挤收费定价原理研究［D］.长春：吉林大学，2007.

［9］ 王孝宏，董洁霜.基于灰关联法的城乡公交分担率影响因素分析［J］. 森林工程，2014（5）：38.

［10］关文忠.森林工业灰度关联分析［J］.森林工程，2007，23（3）：81-84.

［11］王宏，倪志伟，严军，等.灰度关联理论在CBR中的应用研究［J］. 计算机技术与发展，2010，20（5）：96-99.

［12］吴兵，李晔，杨佩昆，等.交通管理与控制第二版［M］.北京：人民交通出版社，2009.

［13］ 杜玉林，闫志刚，杜建华，等.基于灰关联分析的公交分担率预测方法研究［J］. 公路交通科技 （应用技术版），2013（2）：196-201.

［14］陈学武.城市客运交通方式结构预测的层次分析法［J］.东南大学学报：自然科学版，1998，28（3）：23-26.

Model Building of Congestion Charge Based on Gray Correlation Analysis

Dai Zhongna
（Nanjing University of Science and Technology， Nanjing 210094， China）

This paper analyzes the main factors that affect the amount of congestion charge by the gray relational analysis， and then builds the model. The relationship between the congestion charge and multiple impact factors from a small amount of existing data can be studied by this method. And the influence of these factors can be distinguished. It establishes the amount of congestion charge model by fitting the data using SPSS software， which can provide a reference and support for cities which considering congestion charge.

congestion charge amount； gray correlation analysis； model

U491.1+14

A

1672-9889（2015）06-0081-04

戴仲娜（1991-），女，浙江宁波人，硕士研究生，研究方向为交通工程。

（2015-03-06）