区间客运需求组合预测模型研究

韦　达，管　峰，陈田星，李　亮

区间客运需求组合预测模型研究

韦达，管峰，陈田星，李亮

（苏交科集团股份有限公司，江苏 南京 210017）

考虑客运需求受不确定因素影响，导致基于点预测的值不能客观反映未来需求波动。文章采用区间集合方法表示需求不确定，同时结合组合预测方法，建立实际观察值与预测区间中心值偏差最小、预测区间宽度最小的多目标区间需求组合预测模型。以2003—2013年扬中市客运数据为基础进行预测，实例分析表明区间预测结果不仅能包含实际观察值，还能体现未来需求的不确定性，同时误差平方和均值和平均相对误差指标下降也表明区间组合预测模型精度提高，说明该模型的可行性和有效性。

客运需求；不确定；区间集合；组合预测； 多目标规划

公路客运需求预测是公路项目建设重要组成部分。交通需求量预测的准确与否直接关系着项目决策的科学性甚至决定项目的成败［1］。如何准确地预测客运量，是公路项目建设的重要课题，受到越来越多学者和交通规划者的关注。

现有文献对公路客运需求的预测主要集中于点估计，即通过某种或多种组合预测方法得到关于客流量的单一值。常用的点估计预测方法有指数平滑法、回归分析法、马尔可夫分析法、粗糙集法、灰色系统法等单个方法或者多种方法相融合的组合预测。纪跃芝等利用三次指数平滑模型进行长春市客运量的初步预测，并通过季节指数修正预测值［2］；Godfrey等应用指数平滑法建立了客运量预测模型，通过预测值与观察值比较发现预测误差在可接受范围内，验证指数平滑法的可行性［3］；芮海田等将马尔科夫模型与指数平滑法融合提出了新的预测方法，以安徽省统计数据为基础验证［4］；陈坚等引入粗糙集概念对客运量进行预测，模型采用的最简决策规则有效地避免了历年统计数据波动引起的预测误差［5］；杭力等将灰色预测理论与BP神经网络理论相结合，建立组合预测模型［6］；还有学者利用其它方法如多变量状态空间法［7］、模糊神经法［8］、支持向量法［9］等。

以上这些方法都是基于点预计对未来的需求量进行预测。事实上，需求受经济、政治环境等各种因素的影响，预测的单一值不能有效反映未来需求的不确定性，导致决策者不能更加全面把握需求发展趋势。而且，公路基础投资建设耗时长、耗资大的特点，决定其建设不可能经常改变。因此，不准确的需求预测将带来较大风险。基于此，本文采用区间集合表示预测客运需求。区间集合是未来不确定性的表现，其具体方法的应用逐渐成熟［10-13］。同时，为了进一步改善预测效果，本文采用组合预测法。众多文献已经证明组合预测模型相较于单一模型预测精度更高。

综上所述，本文采用区间集合表示客运量不确定性，建立区间需求组合预测模型。最后，通过算例验证模型的可行性与有效性。

1　区间集合

区间集合用A=［a-，a+］表示，其中a-、a+分别称为区间集合的下界和上界。特殊地，若上下界相等时，区间集合就退化为一个实数。区间中心值Ac=（a-+a+）/2，区间半宽为Aw=（a--a+）/2。很显然，下界a-=Ac-Aw，上界a+=Ac+Aw。因此，对于区间集合A还可以利用区间中心值和半宽方式表示：A=［Ac-Aw，Ac+Aw］。

根据文献［13］区间集合A与区间集合B的四则运算和数与区间的加法、乘法运算定义如下：

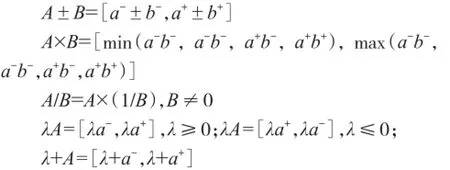
同时，区间运算满足加法交换律，乘法交换律，不满足乘法对加法的交换律。

2　区间客运需求组合预测模型

2.1区间预测

通过式（1）及区间运算法则可以知道若组合权重系数wi为区间集合，记为，则组合测值也一定为区间集合，记为Xt=

显然，基于区间集合的预测结果能表示未来需求不确定性，而且预测结果比单纯的点估计预测精度可靠，也更符合实际情况。

2.2参数说明

根据以上分析，本文采用参数如下：yt表示第t期的实际观察值；表示采用第i种预测方法得到第t期客运需求量值；决策变量表示区间权重系数中心值；表示区间权重系数宽度；表示第t期预测区间中心值表示第t期预测区间宽度。

2.3模型建立

在区间集合条件下，建立多目标公路客运量组合预测模型。相应的目标函数和约束条件如下：

目标函数：

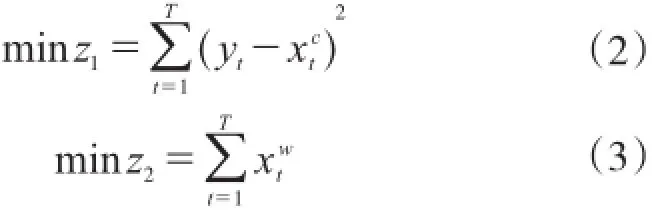
约束条件：

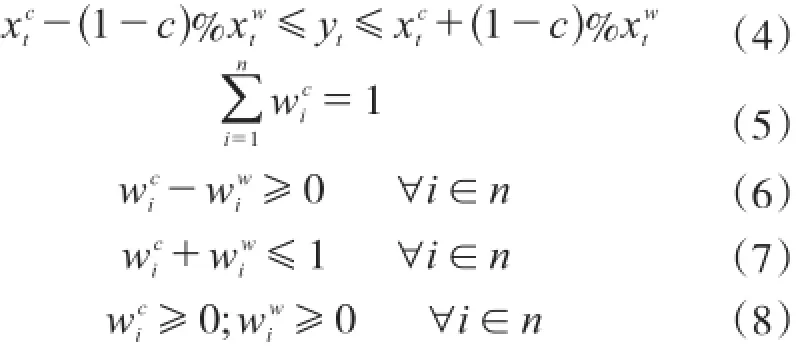
式（2）为目标函数1表示实际观察值和预测区间的中心值偏差最小；式（3）为目标函数2表示预测区间的宽度最小；在实际操作中，若要达到预测区间准确性的目标，必须要保证预测区间中心与实际观察值误差最小，两者越接近说明误差越小；同时预测区间宽度也要最小，区间宽度是不确定性的重要测量依据，区间宽度越大，则不确定性越高。基于以上分析，建立多目标模型。

式（4）表示实际观察值以（1-C）%的置信水平落在预测区间内。本文为了保证求解的预测区间能以较高的概率包含未来的实际值，在预测之前对其进行约束并设置信水平为（1-C）%；式（5）表示各预测方法权重系数区间的中心值和为1；式（6）表示任意权重区间的下界值不低于0；式（7）表示权重区间上界值不高于1；式（8）表示决策变量的非负性。

2.4多目标求解

多目标函数通过将其为单目标进行求解。转化为单目标问题的方法有传统的约束法、分层序列法、功效系数法、评价函数法（理想点法、平方和加权、线性加权等）、以及遗传算法、蚁群算法等。

本文采用评价函数法中的线性加权法进行问题的求解。线性加权法的核心是在各目标函数量纲统一的前提下确定权重系数。由于本文目标函数1和目标函数2的数量量纲不一致，因此，先将其统一。首先求出单独目标函数在约束条件下的最大和最小值分别为n，形成新多目标函数f1、f2：

在此基础上转化为单目标函数为：f =λ1f1+λ2f2，λ1+λ2=1在约束条件（4）～（8）的条件下进行优化求解。

根据以上方法，利用lingo 软件求得各预测方法的权重系数区间中心值和宽度值（即决策变量再通过式（1）可以求得t时期的预测区间

3　实例分析

本文采用江苏省扬中市2003—2013年的客运量统计数据作为基础数据进行模型分析。分别采用趋势外推法、指数平滑法、灰色预测法对历年客运量进行预测，各种预测方法得到的预测数值如表1所示。

本文设定C为2%，则置信水平为98%；假设目标函数权重均为0.5时，验证模型可行性。利用lingo11求得趋势外推法、指数平滑法、灰色预测的权重区间中心值、区间宽度，具体如表2所示。再根据式（1）得到的预测区间及区间中值如表3所示。

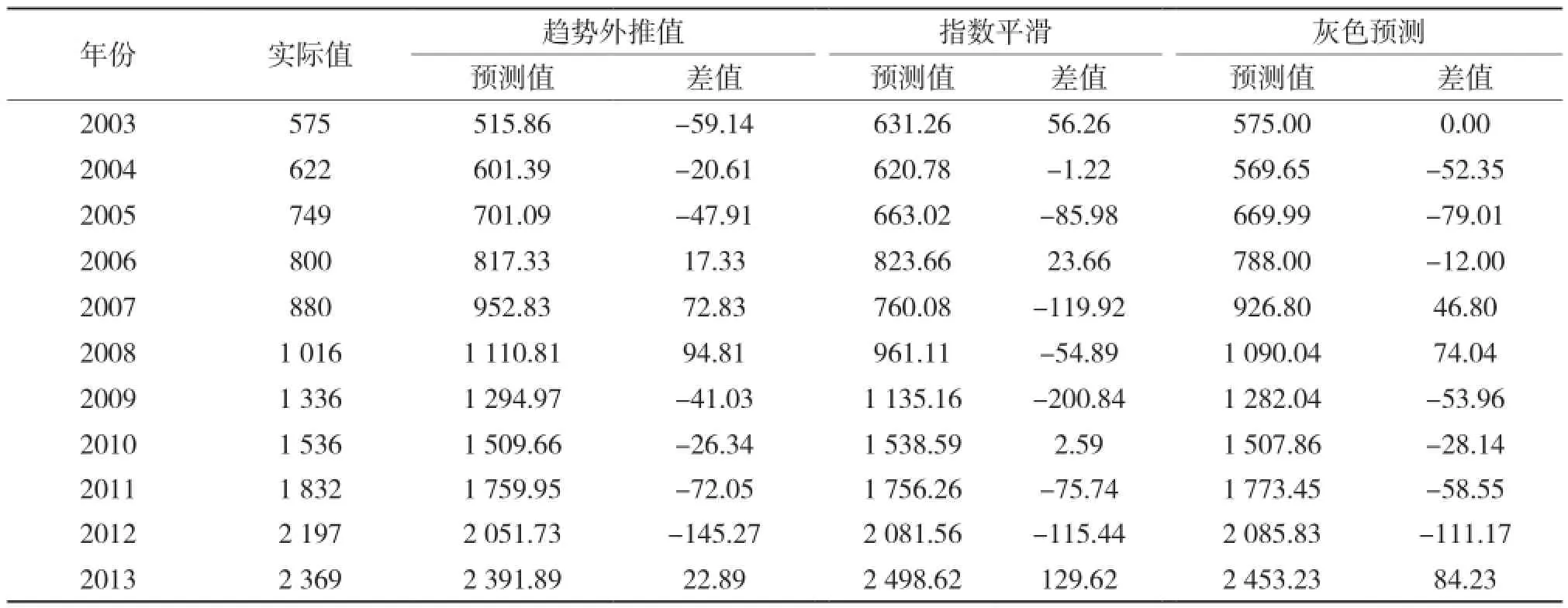
表1　扬中市客运量预测值

表2　各预测方法权重中心值和权重宽度

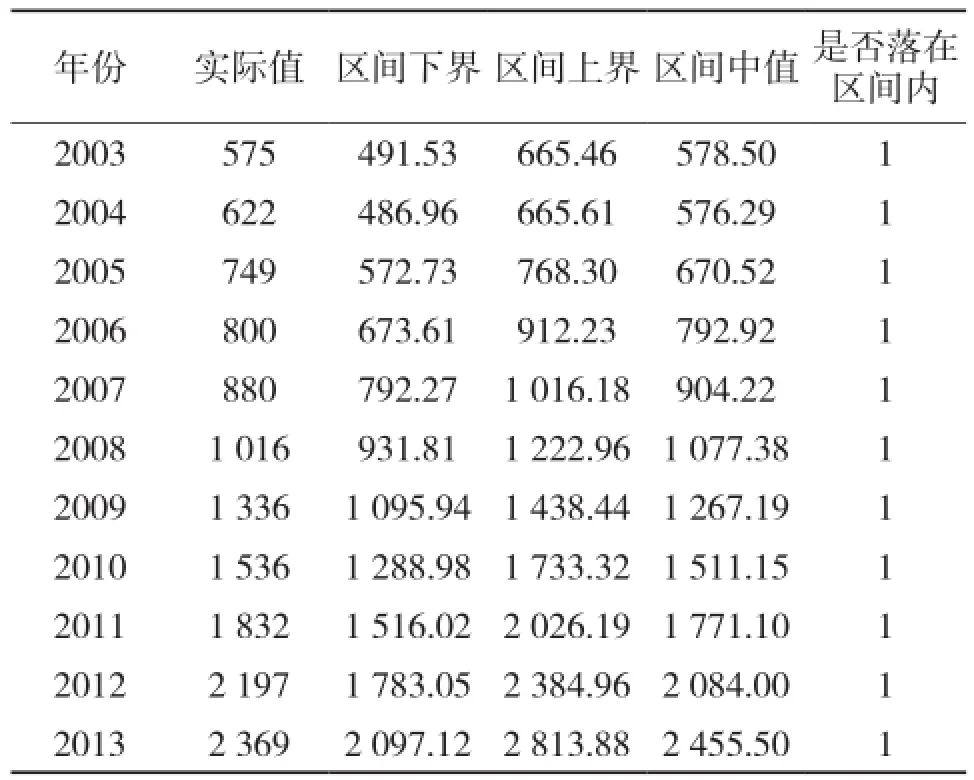
表3　客运量区间预测

通过表3可以发现，2003—2013年的实际客运量均包含于区间内，说明区间预测的可行性。同时，区间需求表明了各种不确定因素对客运量需求预测的影响。

区间预测指标评价图如图1所示。

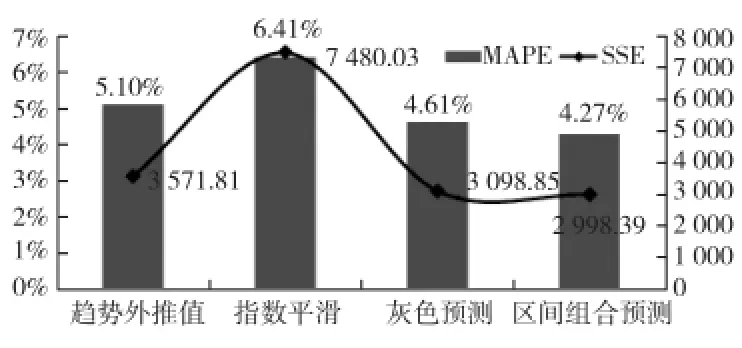
图1　区间预测指标评价图

由图1可知，从MAPE指标看，区间组合预测为4.27%，比灰色预测降低0.4%，比趋势外推降低约1%，比指数平滑降低2%；从SSE指标看，区间预测值为2 998.39，分别比趋势外推法、指数平滑法、灰色预测法降低16.1%、60.0%、32.4%。可以发现区间组合预测评价指标均优于3个单独预测方法，有效地提高了预测精度。说明区间组合预测方法的可行性和有效性。

基于此，对2015年和2016年的客运需求进行预测。首先采用趋势外推法、指数平滑法、灰色预测3种方法预测2015年、2016年的客运量预测值。再根据表2中各预测方法的权重中心值和权重宽度及式（1），得到2015年和2016年客运量的预测区间。具体如表4所示。

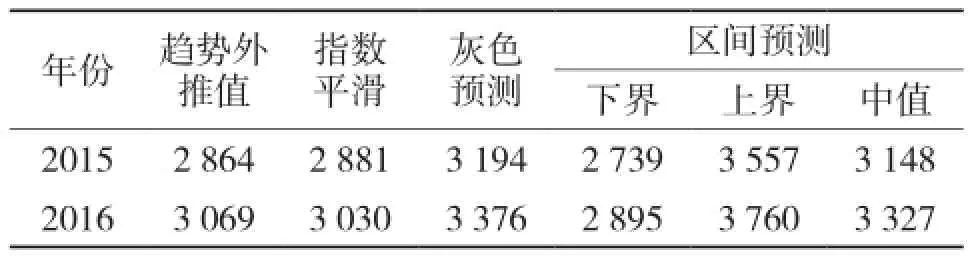
表4　2015和2016年扬中市客运区间预测值

由表4可知，2015年扬中市客运量在［2 739，3 557］区间内，区间中值为3 148；2016年客运量在区间［2 895，3 760］内，区间中值为3 327。显然，通过区间客运需求组合预测模型预测的区间预测值相较于单一的点预测更能体现需求的不确性也更加符合实际情况。

4　结语

本文考虑不确定需求环境下点预测值不能有效反应需求的波动性，认为未来需求是以预测点为中心的区间估计，因此，建立多目标区间需求组合预测模型。通过算例求解发现，区间客运需求组合预测模型不仅可求得未来需求的上下界也能提高模型预测精度，验证了模型的可行性及有效性。

［1］ 王建军，刘建超，陈宽民.公路建设项目交通需求预测与分析［J］.重庆交通学院学报，2004（1）：45-48.

［2］纪跃芝.利用季节指数修正指数平滑预测值对公路客运量进行预测［J］.工科数学，1997（4）：28-31.

［3］Godfrey G A，Powell W B. An adaptive dynamic programming algorithm for dynamic fleet management，I：Single period travel times［J］. Transportation Science，2002，36（1）：21-39.

［4］芮海田，吴群琪，袁华智，等.基于指数平滑法和马尔科夫模型的公路客运量预测方法［J］.交通运输工程学报，2013，（8）：87-93.

［5］陈坚，霍娅敏，傅志妍，等.基于粗糙集的公路客运量预测［J］.重庆交通大学学报，2009（12）：1071-1074.

［6］ 杭力，韩直，杜益文.BP神经网络和GM（1，1）灰色模型在公路客运量预测中的应用［J］.公路交通技术，2006，4（2）：110-113.

［7］Stathopoulos A，Karlaftis M G. A multivariate stat space approach for urban traffic flow modeling and prediction［J］. Transportation Research Part C: Emerging Technologies，2003，11（2）：121-135.

［8］Yin H，Wong S C，Xu J，et al. Urban traffic flow prediction using a fuzzy-neural approach［J］. Transportation Research Part C：Emerging Technologies，2002，10（2）：85-98.

［9］ 陈荔，马荣国.基于支持向量机的都市圈客运量预测模型［J］.交通运输工程学报，2010（12）：75-81.

［10］钟铭，管峰，余璇，等.集装箱班轮轴幅式网络区间模型［J］.大连海事大学学报，2014（4）：49-54.

［11］韩帅，李树刚.基于区间预测模型的流感趋势预测［J］. 计算机仿真，2014（9）：237-242，261.

［12］ Zhao J H，Dong Z Y，Xu Z，etal. A Statistical Approach for Interval Forecasting of the Electricity Price［J］. IEEE Transactions on Power Systems，2008，23（2）：267-276.

［13］Alefeld G. Interval analysis: theory and applications［J］. Journal of Computational and Applied Mathematics，2000（121）：421-464.

Research on Interval Combination Forecasting Model of Passenger Demand

Wei Da， Guan Feng， Chen Tianxing， Li Liang
（JSTI Group， Nanjing 210017， China）

Passenger demand is influenced by uncertain factors， resulting in disability to reflect future fluctuations objectively through forecasting on the basis of point values. It is critical to handle programs of road construction considering decision risks on the basis of demand uncertainty. Demand uncertainty is expressed as interval sets and the forecast model of interval combination is set up with multi-objective. The passenger demand data of Yangzhong city among 2003-2013 is used in the model. The result shows that the model not only includes the actual values， but also reflects the uncertainty. The paper also examines the results with SSE and MAPE index and good precision in forecasting passenger demand is indicated. The model is proved feasible and effective.

passenger demand； uncertainty； interval sets； combination forecasting； multi-objective programming

U491.1+4

A

1672-9889（2015）06-0072-04

韦达（1978-），男，江苏扬州人，工程师，主要从事交通运输规划工作。

（2015-03-01）