几类特殊矩阵方程组的迭代解法收敛性分析

金玲玲，苏岐芳

（台州学院数学与信息工程学院，浙江临海317000）

几类特殊矩阵方程组的迭代解法收敛性分析

金玲玲，苏岐芳*

（台州学院数学与信息工程学院，浙江临海317000）

讨论了线性方程组Ax=b中的系数矩阵A为上三角矩阵、三对角矩阵、严格对角占优矩阵时，Jacobi迭代阵与Gauss-Seidel迭代阵的谱半径之间关系，进而对两种迭代法的收敛速度进行比较.理论分析及数值结果表明，在一定条件下Gauss-Seidel迭代法比Jacobi迭代法收敛较快，这对于求解特殊矩阵方程组时迭代法的选取具有一定的实际意义.

特殊矩阵；收敛；收敛速度

0　引言

在自然科学、工程技术等各领域中，许多问题的解决常常归结于求解线性方程组Ax=b.一般地，求解线性方程组主要有直接解法和迭代解法［1］.经典迭代解法包括Jacobi迭代法、Gauss-Seidel（G-S）迭代法、SOR方法和AOR方法等［7］，其中最常用的方法为Jacobi迭代法和Gauss-Seidel迭代法.

考虑线性方程组

用迭代法解方程组（1），误差估计式

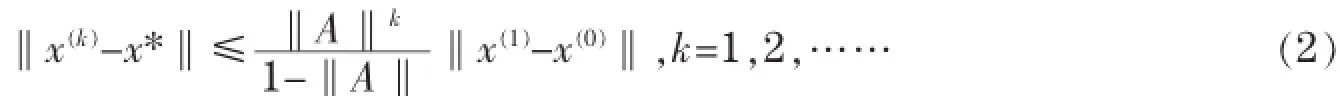
可以看出，‖A‖越小收敛速度越快，且可用来估计迭代次数.

对于线性方程组Ax=b，系数矩阵A=（aij）n×n，aii≠0（i=1，2…n），作分裂：

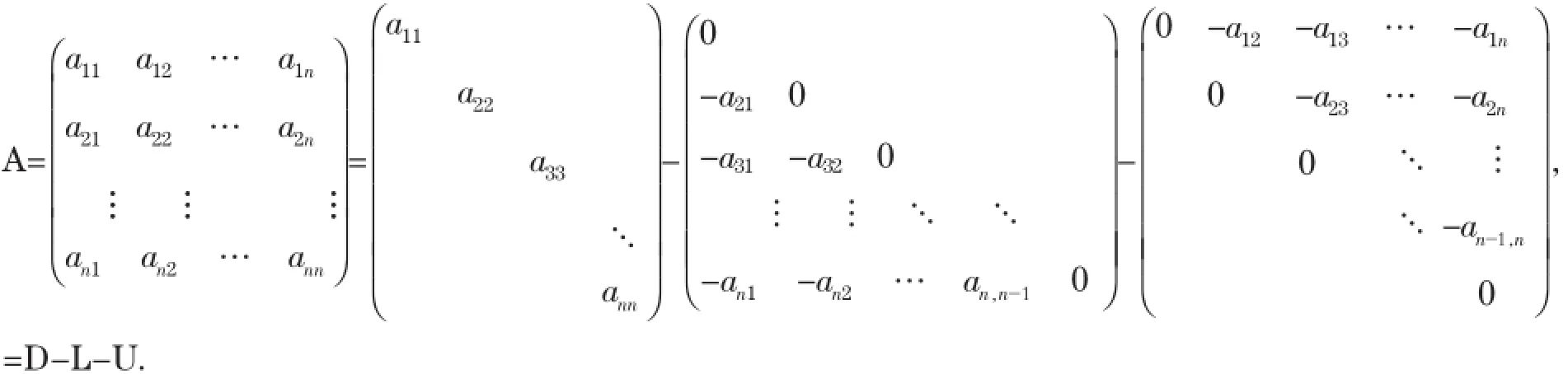
则Jacobi迭代阵为J=D-1（D-A），G-S迭代阵为G=（D-L）-1U［6］.

引理1［1］设有方程组x=Bx+f，及一阶定常迭代法x（k+1）=Bx（k）+f，对任意选取初始向量x（0），迭代法收敛的充要条件是矩阵B的谱半径ρ（B）＜1.

引理2［1］若A为严格对角占优矩阵，则解方程组Ax=b的雅克比迭代法和高斯-赛德尔迭代法均收敛.

引理3［1］设A∈Rn×n，则ρ（A）≤‖A‖，即A的谱半径不超过A的任何一种算子范数.

1　迭代解法及收敛性分析

1.1系数矩阵A为上三角矩阵

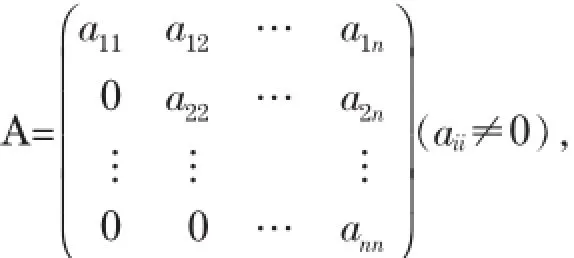
其Jacobi迭代阵和G-S迭代阵分别为

显然，ρ（J）=ρ（G）=0，由引理1可得，解Ax=b的Jacobi迭代法和G-S迭代法均收敛，且收敛速度相同.

1.2系数矩阵A为三对角矩阵

1.A为对称三对角矩阵，且非零元素全都相等设

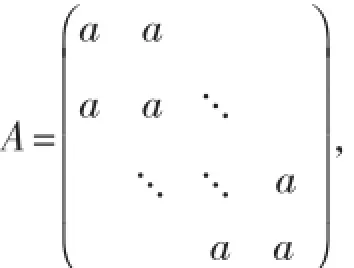
则Jacobi迭代阵

考虑J的特征值，令

则φn（λ）有n个不同的实零点，由于φ2（λ）的零点为-1和1，因此，当n≥3时φn（λ）的最大零点必大于1，

即J的谱半径ρ（J）＞1［4］.因此Jacobi迭代法不收敛.

G-S迭代阵为

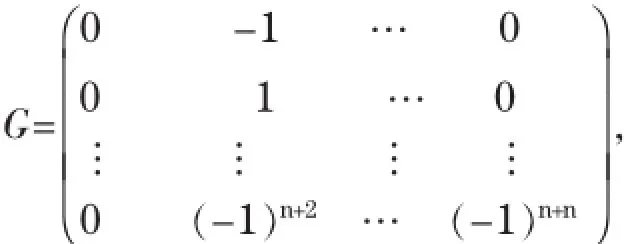
令rij表示矩阵G中的第i行第j列元素，则有

可以证明，ρ（G）≥1（当A为2阶方阵时取等号），因此G-S迭代法不收敛.

2.A为对称三对角矩阵，且三条对角线上的元素分别相等

设aii=a，aij=aji=b，j=i+1，

A为三阶矩阵时

则有

A为四阶矩阵时

则有

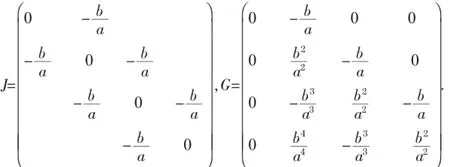
3.A为一般三对角矩阵

A为三阶矩阵时

一般地

则有

其中

当ρ（J）＜1且ρ（G）＜1时Jacobi迭代法和G-S迭代法均收敛.

1.3系数矩阵A为严格对角占优矩阵

1.A的对角线元素全为a，其他元素全为b

由引理2知，Jacobi迭代法和G-S迭代法都收敛.

Jacobi迭代阵为

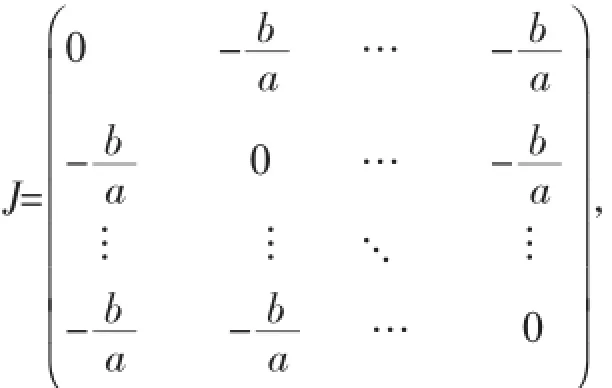
令λI-J=0即

G-S迭代阵为

其中rij表示G的第i行第j列元素.

设矩阵G中第i行元素绝对值的和为Ri，当a，b同号时，，则有

2.A的非对角线元素全为b

Jacobi迭代阵和G-S迭代阵分别为

3.系数矩阵A为一般严格对角占优矩阵

A为二阶矩阵时

A为三阶矩阵时

当对角线上的元素的绝对值都远大于对应行的其他元素的绝对值之和，即时，ρ（J）≈0， ρ（G）≈0，两种迭代法收敛速度基本相同.

2　数值结果

对于线性方程组Ax=b，令

b=（3，-1，0.5，7，2）T，x0=（0，0，0，0，0）T精度为10-5.

例2.1系数矩阵A为上三角矩阵

迭代结果x=（2.0000，-0.1375，1.5500，1.6500，0.4000）T.见表1.

表1　例2.1迭代比较Table.1　The comparison of example 2.1

例2.2系数矩阵A为三对角矩阵

迭代结果x=（-0.7077，0.1693，0.6542，1.0963，3.2692）T.见表2.

表2　例2.2迭代比较Table.2　The comparison of example 2.2

例2.3系数矩阵A为严格对角占优矩阵

迭代结果x=（0.2280，-0.3108，-0.1126，1.1649，0.2061）T.见表3.

表3　例2.3迭代比较Table.3　The comparison of example 2.3

3　结论

对于系数矩阵为上三角矩阵，Jacobi与Gauss-Seidel迭代法都收敛且收敛速度相同.对于系数矩阵为三对角矩阵时，在两种迭代法都收敛的情况下，在一定条件下Gauss-Seidel迭代法比Jacobi迭代法收敛较快.对于系数矩阵为严格对角占优矩阵时，Jacobi与Gauss-Seidel迭代法都收敛且在一定条件下Gauss-Seidel迭代法收敛较快，当对角线上的元素的绝对值都远大于对应行的其他元素的绝对值之和时，两种迭代法的收敛速度基本相同.

［1］李庆扬，王能超，易大义.数值分析［M］.5版.北京：清华大学出版社，2008.

［2］宋海洲，徐强，田朝薇.计算非负不可约矩阵谱半径的新算法［J］.华侨大学学报，2011，32（3）:348-351.

［3］杨胜良.三对角矩阵的特征值及其应用［J］.工科数学，2010，40（3）:155-160.

［4］蒋尔雄.矩阵计算［M］.北京：科学出版社，2008.

［5］郭世平.广义对角占优矩阵的若干基本性质［J］.安徽教育学院学报，2005，23（6）:6-9.

［6］胡家赣.线性代数方程组的迭代解法［M］.北京：科学出版社，1997.

［7］Richard L B，Faires J D.数值分析［M］.7版.北京：高等教育出版社，2001.

［8］易大义，云宝，李有法.计算方法［M］.杭州：浙江大学出版社，2002.

［9］马云.数值分析中的迭代法解线性方程组［J］.南京师范大学学报，2010（50）:71-72.

［10］刘长河.解线性方程组的迭代方法研究［J］.北京建筑工程学院学报，2013（04）:65-67.

［11］李华.非负矩阵谱半径的新界值［J］.长江大学学报，2012，9（12）:1-8.

［12］赵丹.雅可比迭代法与高斯-塞德尔迭代法研究［J］.兴义民族师范学院学报，2012（2）:108-112.

［13］田秋菊.迭代矩阵谱半径的上界［J］.辽宁石油化工大学学报，2008，28（3）:79-82.

［14］Changbum Chun.A two-parameter third-order family of methods for solving nonlinear equations of nonlinear equations.Applied Mathematics and Computation.2007，189:1822-1827.

［15］Muhammad Aslam Noor，Muhammad Waseem.Some iterative methods for solving a system of nonlinear equations.Computers and Mathematics with Applications.2009，57:101-106.

（责任编辑：耿继祥）

The Convergence Analysis of Iterative Methods for Systems with Some Special Matrices

JIN Lingling，SU Qifang*
（School of Mathematics and Information Engineering，Taizhou University，Linhai 317000，China）

In this paper，we discuss the relationship of spectral radius of Jacobi and Gauss-Seidel iterative matrices for solving systems of linear equations Ax=b which has special matrix，containing upper triangular matrix，tridiagonal matrixand strictly diagonally dominant matrix，etc.，compare the convergence rate for Jacobi and Gauss-Seidel iterative methods.Theoretical analysis and numerical results show that in general，the convergence speed of the Gauss-Seidel iterative method is equal to or greater than that of Jacobi iterative method.The solution has a certain practical significance for solving special system of linear equations.

special matrix；convergence；the rate of convergence

10.13853/j.cnki.issn.1672-3708.2015.06.002

2015-05-04；

2015-06-13

简介：苏岐芳（1964-），女，黑龙江绥化人，副教授，主要研究计算数学。