黏土含水率空间分布规律的模型试验研究*

刘子振，苏洪健，刘娇，陈文龙

（台州学院建筑工程学院，浙江台州318000）

黏土含水率空间分布规律的模型试验研究*

刘子振，苏洪健，刘娇，陈文龙

（台州学院建筑工程学院，浙江台州318000）

黏土含水率对土体粘聚力影响较大，且会影响雨水入渗边坡过程，进而影响到边坡的稳定性。本文通过模型试验，获得了黏土含水率随深度的空间变化关系，并拟合了含水率的深度函数关系。结果表明：表面水平且无地下水位时，黏土含水率随深度变化较小，可近似按直线拟合；表面水平且有地下水位时，深度超过10cm后，含水率变化较明显，含水率随深度可按二项式拟合；无地下水位时坡面下深20cm以内含水率变化较大，含水率不稳定，若含水率随深度按线性拟合，坡脚处变化较小，而坡顶和坡中处变化较大。

黏土含水率；模型试验；深度；黏土边坡；拟合式

土体物理力学参数是基坑稳定和边坡稳定性的关键要素，而土体的含水率对其物理力学性质又有较大的影响。通常，在边坡稳定性研究中只考虑土中含水率是均一的。然而，根据土壤和水的特性，不同深度处的含水率是不一样。如果天然条件下土中含水率看成均一的，对土体参数的选取不利，必将影响到基坑稳定或边坡稳定性计算结果，导致原本不稳定边坡的计算结果却是稳定的。因此，需要结合试验，测得土体含水率随深度的空间变化关系，为工程所需参数提供参考。

Green等［1］研究了空气和水通过土体的过程和作用机理，并建立了三者的相互影响关系，体现了水在土体中作用结果。谢志清等［2］对比分析了不同下垫面条件下的土壤含水率时空变化特征，并进行了拟合，结果表明，夏季土壤水分在湿润区呈单峰偏态分布，在非均匀地表条件下，土壤表层水分分布的空间变化率相当大。赵景波等［3］研究了青海湖某镇的土壤水与土壤水库，发现土壤含水率随着深度的增加而减少，在0.6m深度以下土壤含水率严重不足。陈洪松等［4］研究了土壤初始含水率对坡面雨水入渗的影响，揭示了湿润锋运移和水分再分布规律。他们认为初始含水率均匀分布条件下，雨水入渗与再分布过程中湿润锋面平行坡面垂直向下整体运移，可以简化为一维分析；如果初始含水率非均匀分布，初始含水率越高，湿润锋的运移速率也越大。降雨入渗边坡时，土体的湿润程度和范围对湿润锋的运移速率有一定的影响，坡面雨水对入渗有一定的促进作用。陈赟等［5］设计和应用TDR联合监测土体含水率的传感器，能在现场快速测定土体含水率以及在土体不同深度的变化情况，且测试结果可靠。毛丽丽等［6］采用水平土柱和修正的Green-Ampt模型分析土壤入渗性，认为土壤入渗能力与地下水有密切关系，提出的修正模型能很好地描述水分在土壤中的分布。方文松等［7］认为土壤的初始湿度对雨水入渗深度影响最大，并建立了降雨量与雨水入渗度的线性关系。陈伟等［8］分析了非饱和土边坡降雨入渗过程，并研究相应的最大入渗深度，获得了降雨入渗非饱和土边坡的最大入渗深度公式，认为坡面土最大含水率要略小于饱和含水率。

综上所述，土体内的含水率是变化的，对雨水入渗有一定的影响。然而针对边坡黏土含水率变化在边坡稳定性的影响研究中仍较少，本文通过黏土含水率空间测试分析，为黏土边坡稳定性分析提供参考。

1　试验方案

将某山坡处取回的黏土，分成三组，分别装入两个圆桶和边坡模型中，其中一个圆桶设置有地下水位。黏土样按要求进行分层压实，然后，将桶口用塑料膜包裹，边坡自由面放置少量杂草，边坡模型做好后用防雨布遮盖。将黏土样模型自然放置约75天（4月23日到7月6日），如图1所示。为了防止水分蒸发和流失，要求及时取样并测定黏土含水率。

图1　黏土样试验模型

2　测试结果与分析

2.1水平面下黏土含水率分布

通过试验测得初始的黏土样相关参数，如表1所示。

表1　初始黏土样相关参数

根据试验方案，装土圆桶内深75cm，桶口直径115cm，在桶底面铺设15cm厚的碎石。其中一个桶中央垂直插入一根直管，用来补充地下水位，沿桶四周布设32个出水孔，保证桶中水位深恒定在15cm。圆桶作好深度标尺，通过取土器标定取土深度。水位设置和深度标尺如图2所示。各孔按垂直深度每隔5cm取一次土，并及时进行取样、称重、烘干。

图2　水位控制和深度标尺（单位：cm）

土样静置一段时间后，同时对两圆桶表层黏土进行室内实验，测得黏土的相关参数如表2所示。然后，按垂直深度进行取样，进行含水率测试，每桶钻三个孔取样，孔口按正三角分布，如图3所示。无地下水位的黏土含水率测试结果如图4所示，有地下水位的黏土含水率测试结果如图5所示，将不同孔号在相同深度处含水率进行比较，如图6所示。

表2　圆桶内黏土相关参数

图3　取土孔分布与成孔情况

由图4可知，无地下水位时，总的平均含水率为27.3%。1#孔含水率最小值为24.8%、最大值为27.7%，平均含水率为26.6%；2#孔含水率最小值为26.0%、最大值为28.7%，平均含水率为27.6%；3#孔含水率最小值为26.9%、最大值为28.4%，平均含水率为27.6%。孔的含水率随深度有变化，变化率分别为

5.4%、9.8%、10.9%，最大含水率为28.7%。拟合线型可按直线式，因此，根据实际可采用平均含水率。

图4　无地下水位时黏土含水率随深度变化

由图5可知，有地下水位时，总的平均含水率为29.1%。4#孔含水率最小值为25.3%、最大值为35.8%，平均含水率为27.7%；5#孔含水率最小值为26.5%、最大值为34.7%，平均含水率为29.3%；6#孔含水率最小值为26.6%、最大值为41.2%，平均含水率为30.2%。黏土含水率随深度有很大的变化，变化率分别为37.9%、28.0%、48.3%，最大含水率41.2%比孔表层土含水率26.6%多14.6%、比无地下水位表层含水率26.9%多14.3%。拟合线型，按二项式拟合比线性和指数式更合理，因此，不可采用均一的平均含水率。

由图6可知，无地下水位时，在同一深度处各孔的含水率变化较小；有地下水位时，表层10cm深度内，在同一深度处各孔的含水率变化较小，超过10cm深度后，同一深度处各孔的含水率变化较明显，且随深度增加更加明显。

图5　有地下水位时黏土含水率随深度变化

2.2边坡黏土含水率分布

黏土坡体尺寸：坡高60cm、坡角39.1°、横向宽70cm。模型底部铺6cm厚的碎石砂土，且底模没有出水孔，间距15cm。边坡模型及深度标尺如图7所示。测试时按一定深度，分别在坡顶、坡中和坡脚三个部位采用取土器取土，并及时进行取样、称重、烘干。通过试验获得黏土相关物理力学参数如表3所示，边坡不同深度黏土的含水率如图8所示，将含水率随深度进行拟合，如图9所示。

表3　模型边坡黏土相关参数

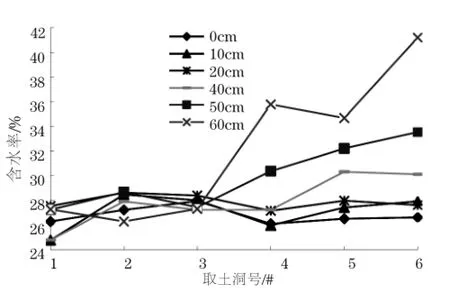
图6　不同孔号同深度下含水率

图7　边坡模型及深度标尺（单位：cm）

由图8可知，黏土总的平均含水率：坡顶7#为24.4%、坡中8#为24.3%、坡脚9#为25.1%；坡顶7#孔含水率最小值为23.1%、最大值为26.6%，平均含水率为24.4%；坡中8#孔含水率最小值为23.2%、最大值为25.8%，平均含水率为24.3%；坡脚9#孔含水率最小值为23.9%、最大值为26.7%，平均含水率为25.1%。各孔的含水率随深度的变化范围接近，含水率随深度有变化，变化率分别为14.4%、10.7%、11.2%，含水率变化率比平面分布情况要大。最大含水率26.7%比孔表层土含水率23.1%多3.6%，如果有地下水位时可能会更大。黏土表面深20cm以内含水率变化较大，表面含水率不稳定，深大于20cm处的含水率随深度变化幅度较小。

图8　边坡不同深度处黏土的含水率

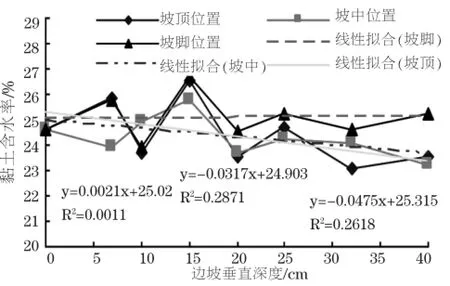
图9　边坡黏土含水率拟合情况

由图9可知，只有坡脚处含水率随深度变化较小，而坡顶和坡中处变化较大。因此，边坡稳定性分析时应尽可能考虑黏土含水率变化，从而可以采用更合理的黏土物理力学参数。

3　结论

（1）通过试验获得黏土体含水率随深度的空间变化关系，并拟合了含水率的深度函数关系。

（2）表面水平且无地下水位时，黏土含水率随深度变化较小，可按直线拟合，在同一深度处各孔黏土的含水率变化较小；表面水平且有地下水位时，表层深度10cm内，在同一深度处各孔的含水率变化较小，深度超过10cm后，含水率变化较明显，最大变化量为15.9%，含水率随深度可按二项式拟合。

（3）坡面下深20cm以内含水率变化较大，表层含水率不稳定，深大于20cm处的含水率随深度变化幅度较小。若含水率随深度按线性拟合，坡脚处含水率随深度变化较小，而坡顶和坡中处变化较大。

［1］Green WH，Ampt CA.Studies on soil physics:The flow of air and water through soils［J］.J Agric.Sci.，1911，（4）:1-24.

［2］谢志清，丁裕国，刘晶淼.不同下垫面条件下土壤含水量时空变化特征的对比分析［J］.南京气象学院学报，2002，25（5）:625-632.

［3］赵景波，马淑苗，马延东，等.青海湖北沙柳河镇土壤水与土壤水库研究［J］.资源科学，2012，34（6）:1095-1100.

［4］陈洪松，邵明安，王克林.土壤初始含水率对坡面降雨入渗及土壤水分再分布的影响［J］.农业工程学报，2006，22（1）:44-47.

［5］陈赟，陈伟，陈仁朋，等.TDR联合监测土体含水率和干密度的传感器的设计及应用［J］.岩石力学与工程学报，2011，30（2）: 418-426.

［6］毛丽丽，雷廷武，刘汗，等.用水平土柱和修正的Green-Ampt模型确定土壤的入渗性能［J］.农业工程学报，2009，25（11）:35-38.

［7］方文松，刘荣花，朱自玺，等.农田降水渗透深度的影响因素［J］.干旱地区农业研究，2011，29（4）:185-189.

［8］陈伟，莫海鸿，陈乐求.非饱和土边坡降雨入渗过程及最大入渗深度研究［J］.矿冶工程，2009，29（6）:13-17.

（责任编辑：耿继祥）

An Experimental Study of Clay Model for Spatial Distribution Rule of Moisture Content

LIU Zizhen，SU Hongjian，LIU Jiao，CHEN Wenlong
（School of Civil Engineering and Architecture，Taizhou University，Taizhou 318000，China）

The cohesive of clay is influenced greatly by the moisture content.And the moisture content could affect the process of rainfall infiltration into side slope，which affects the stability of the slope.

In this paper，through model test，the relationship and fitted function of the clay moisture content to the depth could be obtained.The results show that the change of clay moisture content with depth is small under the surface level and without underground water.And the relationship of moisture content to the depth could be fitted linear.Under the surface level and underground water，the change of moisture content is more obvious after more than 10 cm depth.And the moisture content with depth could be fitted according to the binomial function.The moisture content is unstable within 20 cm depth with underground water level of clay slope.The change of moisture content is smaller at the foot of slope，bigger at the top and middle of slope surface if the relationship of moisture content to the depth could be fitted linear.

moisture content of clay；model test；depth；clay slope；fitting formula

10.13853/j.cnki.issn.1672-3708.2015.06.008

2015-10-12

浙江省自然科学基金资助项目（LY13E080008）；浙江省新苗人才计划项目（No.2013R428026）。

刘子振（1979-），男，江西永丰人，副教授，博士，主要从事岩土工程等方面的研究与教学工作。