一类级联系统的微分无源性
康剑灵, 张 晖, 叶华文
(1. 东华大学 理学院, 上海 201620; 2. 中南大学 信息科学与工程学院, 湖南 长沙 410083)
一类级联系统的微分无源性
康剑灵1, 张晖1, 叶华文2
(1. 东华大学 理学院, 上海 201620; 2. 中南大学 信息科学与工程学院, 湖南 长沙 410083)
微分无源性将微分存储函数和微分李雅普诺夫函数联系起来,是研究非线性系统稳定性的有力工具.通过判断系统解之间的距离研究系统解的跟踪、同步等问题.研究了一类级联系统的微分无源性,讨论了保证系统具有微分无源性的条件,并给出这类级联系统具有的一些性质.
微分无源性; 微分存储函数; 级联系统; 延拓系统
2013年,在收缩理论[1]基础上,文献[2]通过提升李雅普诺夫函数到切丛上,建立了非线性系统理论的微分李雅普诺夫框架,并以此来研究系统的增量稳定性.在此框架下,文献[3]通过提升存储函数和供给率到系统流形的切丛上,又给出了系统微分耗散的思想,介绍了系统的增量耗散性.同时,文献[4]基于非线性延拓系统(即原非线性系统和其变分系统)的几何结构建立了系统的微分无源理论. 文献[5]通过对一类物理系统的微分无源性的讨论,给出有对偶能量的梯度系统非线性电路Baryton-Moser系统保持微分无源的几何条件.
上述的各种微分方法都将稳定性从初始解到目标解(即平衡态)的距离研究转化为任意两个解之间的距离研究,这种忽略初始解和目标解状态的方法被用在跟踪调节[6]、观测器设计[7]、同步[8]等问题中.
本文在文献[2-3, 5]的基础上研究一类级联系统保持微分无源性的几何条件.下面介绍一些记号和定义.
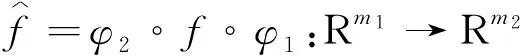
定义1非线性系统
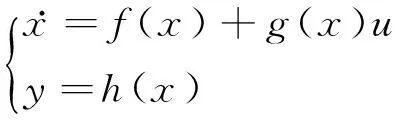
(1)
其中:状态空间为M,输入空间U⊂Rm,输出空间Y⊂Rm,x∈M,u∈U,y∈Y.f和g是向量场,映射h:M→Y.其变分系统为
(2)
称系统(1)和(2)的合并系统为系统(1)的延拓系统.
定义2Ω是M的孤立点集,对任意的x∈M,TxM可以分为垂直分布Vx⊂TxM,和水平分布Hx⊂TxM的直和,即Vx⊕Hx=TxM,其中vi(1≤i≤r)和hi(1≤i≤k)是C1向量场.
Vx=span{v1(x),v2(x), …,vr(x)},
0≤r (3) Hx=span{h1(x),h2(x), …,hk(x)}, 0≤k (4) 若存在c1,c2∈R≥0,p∈R≥1和函数F:TM→R≥0,使对任意的(x,δx) ∈TM都有 c1F(x,δx)p≤δS(x,δx)≤c2F(x,δx)p (5) 则称函数δS:TM→R≥0是系统的微分存储函数. δS和F必须满足以下条件:任给一孤立点集Ω⊂M, (ⅰ) 对任意的x∈M,δx∈Hx{0},δS和F是C1的; (ⅱ) 对任意的(x,δx)∈TM,使得(x,δx)=(x,δxh)+(x,δxv),其中δxh∈Hx,δxv∈Vx,满足δS(x,δx)=δS(x,δxh),δF(x,δx)=δF(x,δxh); (ⅲ) 对任意的x∈MΩ,δx∈Hx,满足F(x,δx)>0; (ⅳ) 对任意的λ>0,x∈M,δx∈Hx,满足F(x,λδx)=λF(x,δx); (ⅴ)F(x,δx1+δx2) 定义3如果系统(1)存在微分存储函数δS,使得对所有的t≥0,延拓系统的所有解(x,y,u,δx,δy,δu)满足: δS(x(t),δx(t))-δS(x(0),δx(0))≤ (6) 则称系统(1)是微分无源的. 假设δS∈C1,不等式(6)两边同时对t求导可得 则称系统为增量稳定的. 考虑下面的级联系统: (7) 根据文献[3],可以得到系统(7)的变分系统: (8) 系统(7)和(8)的合并系统为系统(7)的延拓系统,其中状态(x1,x2,δx1,δx2)∈TM,输入(u,δu)∈TU,输出(y,δy)∈TY. 对于系统(7)的任意解(x1,x2,u,y),系统(8)中的解(δx1,δx2,δu,δy)是解(x1,x2,u,y)的无穷小变分,即(δx1,δx2,δu,δy)是(x1,x2,u,y)和其他解的无穷小误差.更加直观地可以看到,当(δx1,δx2)收敛到0时,系统(7)中的解互相收敛.文献[1]基于李雅普诺夫方法,研究了δx的收缩性和稳定性之间的关系. 本文在文献[2-3]的基础上研究上述级联系统的微分无源性,即这类级联系统具有微分无源性的条件以及保持微分无源性的级联系统所具有的几何性质及物理意义. 定理1如果系统(7)是微分无源的,且具有微分存储函数δS∈C1,当对任意的x∈M都有垂直分布Vx=0时,系统(7)是增量稳定的. (9) 由定义4可知,系统(7)是增量稳定的. (10) (11) (12) (13) 证明:要使 g2(x2)δu≤δy(t)Tδu(t). g2(x2)δu=δy(t)Tδu(t) 根据条件(a)和(b)易得式(10). 条件(e)化简后即为式(12). 比较上面等式左右两边即得式(13). 证毕. 定理1中的式(9)保证系统在u=0时,系统自身具有收敛性,即系统的稳定性由度量M1和M2(即驱动系统和被驱动系统)的稳定性决定,其中式(10)表示级联项能量需要随着时间t递减. 式(11)限制了度量矩阵M2(x2)的范围,因为g2(x2)的性质决定了M2(x2).同样根据式(12),可以得到输出y的形式. (14) (15) (16) 证毕. (17) (18) (19) (20) 证明类似命题1的推导. 例1考虑线性级联系统 (21) 它的变分系统为 (22) 本文在非线性系统的几何控制理论框架下,研究了一类级联系统微分无源的几何结构,但未对系统的稳定性进行讨论.后续将针对一些实际的级联系统模型基于微分无源性进行系统的稳定性研究,并将针对一些特殊的非线性系统讨论其微分无源性结构及其稳定性. [1] LOHMILLER W, SLOTINE J E. On contraction analysis for non-linear systems[J]. Automatica, 1998, 34(6):683-696. [2] FORNI F, SEPULCHRE R. A differential lyapunov framework for contraction analysis[J]. IEEE Transactions on Automatic Control, 2014, 59(1):614-628. [3] FRONI F, SEPULCHRE R. On differentially dissipative dynamical systems[C]//In 9th IFAC Symposium on Nonlinear Control Systems. 2013:15-20. [4] VAN DER SCHAFT A J. On differential passivity[C]//In 9th IFAC Symposium on Nonlinear Control Systems. 2013: 21-25. [5] FORNI F, SEPULCHRE R, VAN DER SCHAFT A J. On differential passivity of physical systems[C]//52nd IEEE Conference on Decision and Control. 2013: 6580-6585. [6] PAVLOV L, MARCONI L. Incremental passivity and output regulation[J]. Systems and Control Letters, 2008, 57(5):400-409. [7] AGHANNAN N, ROUCHON P. An intrinsic observer for a class of lagrangian systems[J]. IEEE Transactions on Automatic Control, 2003, 48(6):936-945. [8] WANG W, SLOTINE J E. On partial contraction analysis for coupled nonlinear oscillators[J]. Biological Cybernetics, 2005, 92(1):38-53. Differential Passivity for a Class of Cascade Systems KANGJian-ling1,ZHANGHui1,YEHua-wen2 (1. College of Science, Donghua University, Shanghai 201620, China; 2. College of Information Science and Engineering, Central South University, Changsha 410083, China) Differential passivity analysis can combine the differential storage function and differential Lyapunov function to study the stability of nonlinear systems. By judging the distances between the solutions of the system, it can be used to discuss the solution tracking and synchronization problems of the system. The passivity theory for a class of cascade system is studied. It is investgated for the conditions which can guarantee the differential passivity of the given system.Some properties are also given for this kind of cascade system. differential passivity;differential storage function;cascade system;prolonged system 1671-0444(2015)06-0857-05 2014-09-16 国家自然科学基金资助项目(61104125);中央高校科研业务经费资助项目(11D10911) 康剑灵(1972—),女,江西赣州人,副教授,博士,研究方向为非线性系统几何控制理论.E-mail:kangjl@dhu.edu.cn O 231.2 A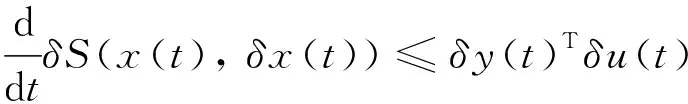
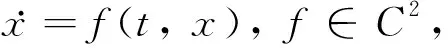
1 系统模型介绍
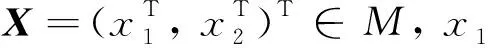
2 主要结果
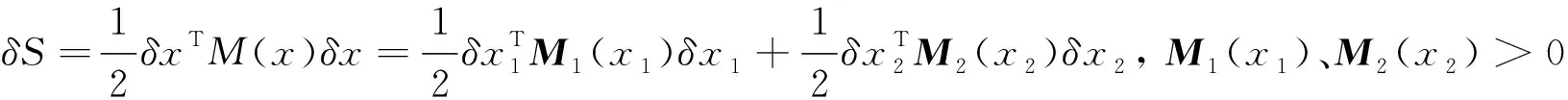
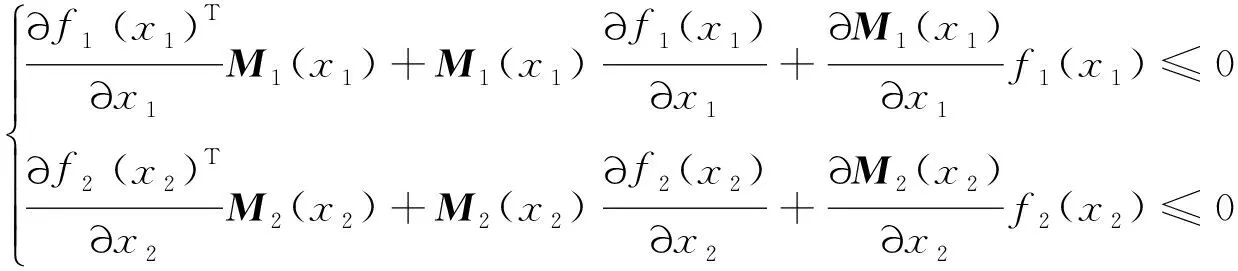
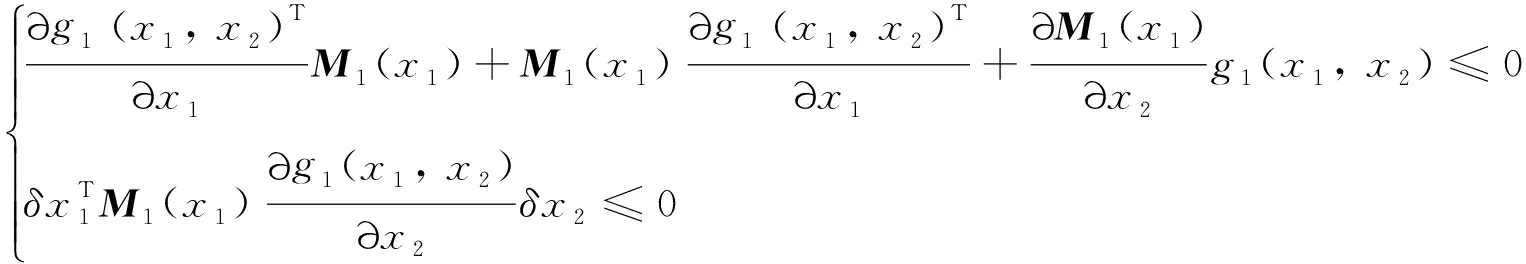
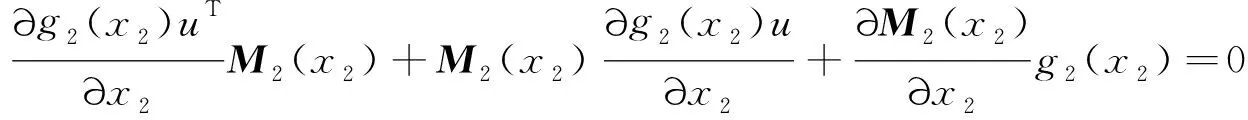
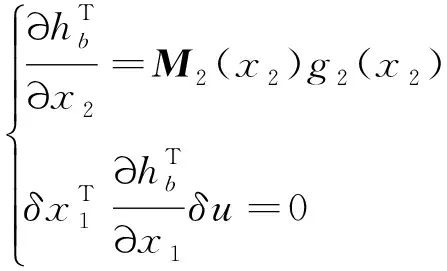
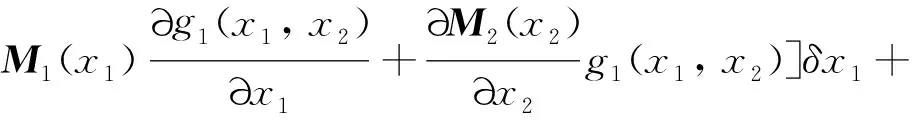
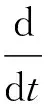
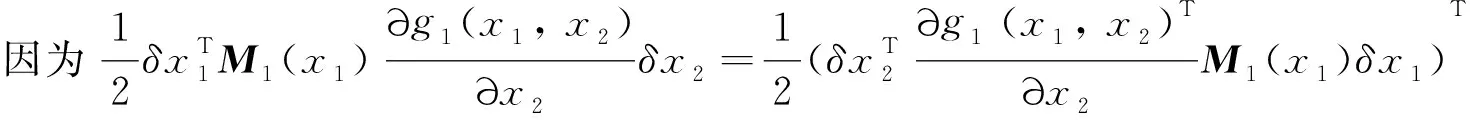
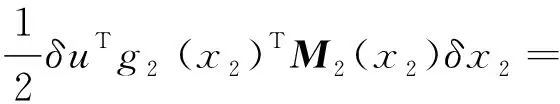
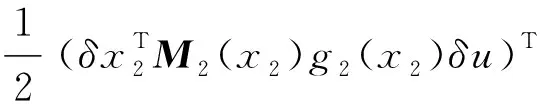
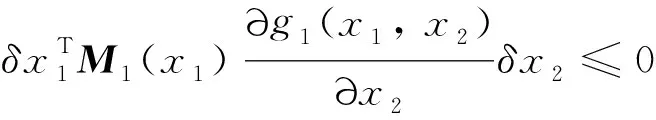
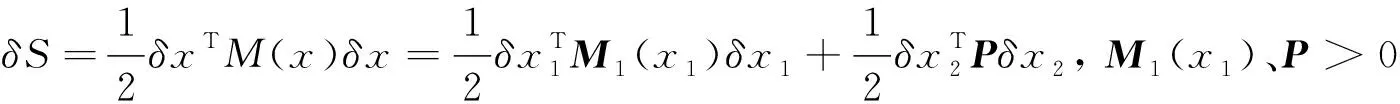
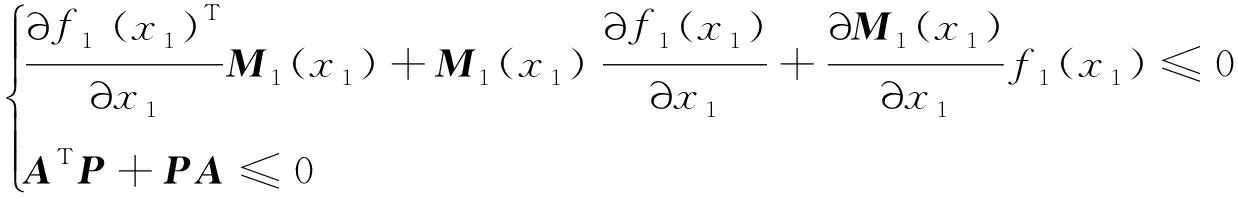
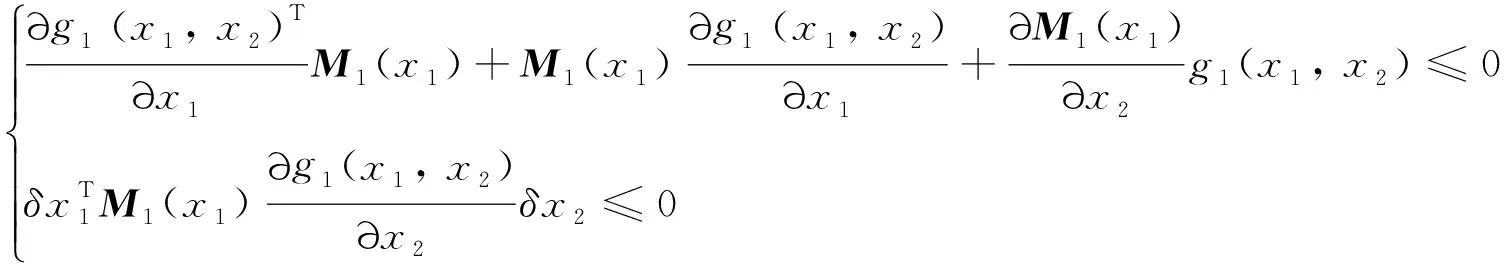
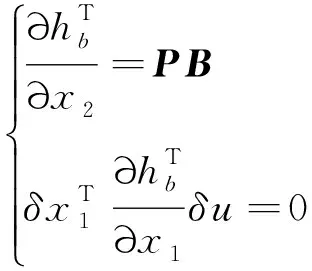
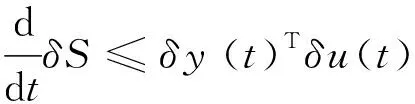
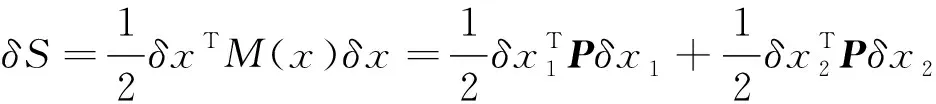
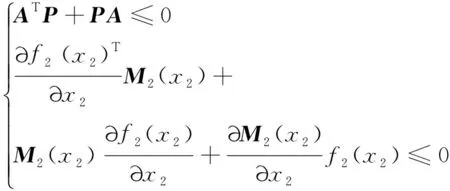
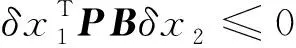
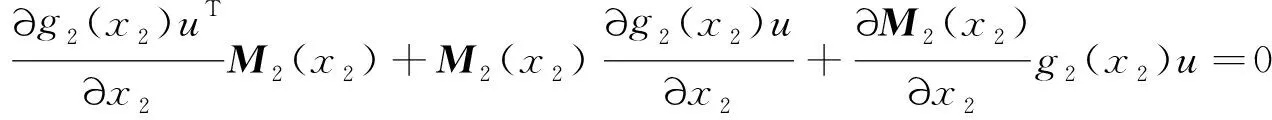
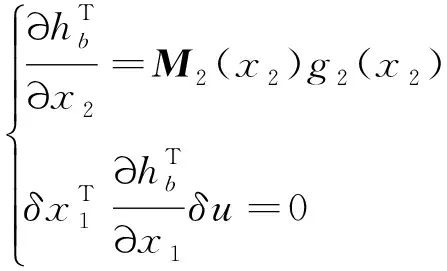
3 结 语

