1自由度8杆单铰LEMs构型的研究

王　强， 曹　毅, 2, 3, 4， 陈桂兰

(1. 江南大学 机械工程学院， 江苏 无锡 214122；

2. 上海交通大学 机械系统与振动国家重点实验室， 上海 200240；

3. 哈尔滨工业大学 机器人技术与系统国家重点实验室， 黑龙江 哈尔滨 150080；

4. 江苏省食品先进制造装备技术重点实验室， 江苏 无锡 214122)

1自由度8杆单铰LEMs构型的研究

王强1， 曹毅1, 2, 3, 4， 陈桂兰1

(1. 江南大学 机械工程学院， 江苏 无锡 214122；

2. 上海交通大学 机械系统与振动国家重点实验室， 上海 200240；

3. 哈尔滨工业大学 机器人技术与系统国家重点实验室， 黑龙江 哈尔滨 150080；

4. 江苏省食品先进制造装备技术重点实验室， 江苏 无锡 214122)

提出一种Lamina Emergent Mechanisms(LEMs)机构综合方法，对1自由度8杆LEMs构型进行研究，该方法能够求解包含单铰转动副，以及机架和主动件变换的LEMs机构综合问题.首先，通过构造平面运动链的杆组邻接矩阵，求解基于1自由度8杆的所有平面机构的可能连接方式.其次，基于杆件和自由度的数目，分析包含各级Assur杆组的所有装配方式，构建杆组邻接矩阵的框架.再次，依据一定的约束条件，将第一级及之后的杆组依次装配到主动件和机架或者前级杆组上，并且同步辨识同构体，从而获取仅含转动副的所有平面机构构型.最后，用相应的柔顺片段代替刚性片段，完成LEMs构型综合.

平面折展柔顺机构(LEMs)； 机构综合； 邻接矩阵

Lamina Emergent Mechanisms(LEMs)是由美国学者Larry L. Howell及其团队提出的一种从平面材料中制造，并且能够浮出制造平面的新型机构[1].此种机械装置通过使柔性部位变形来实现所需的运动，因此是一种柔顺机构.LEMs在拥有其他柔顺机构优点的同时，具有以下无可比拟的优势：(1)用简单的拓扑结构实现精密复杂的机械任务；(2)采用成本较低的加工工艺(如剪切、冲孔、落料等)进行加工；(3)LEMs的平面特性使得其在储藏和运输成本方面亦颇具优势.图1所示为一种4杆LEMs，采用了一种平面转动副——Lamina Emergent Torsion (LET).

图1　一种4杆LEMsFig.1　A four-bars LEMs

目前国内外研究主要集中于LEMs的运动副设计及驱动方式的选择.文献[2]设计了一种目前常用的转动副LET，该转动副通过材料的变形获得所需运动.文献[3]研究了两种适用于金属薄板的转动副RUFF(Revolute U-form Flexure)和TUFF(Torsional U-form Flexure).文献[4]提出了一种能同时承受拉、压应力的转动副.文献[5]基于刚体代替法设计了新型多层LEMs，并且运用伪刚体模型和LET的弹簧刚度模型，对其进行输入输出之间关系的研究.

由于构件数目相同，并且能够实现确定的相对运动的机构不止一种，所以产生了如何选择的问题，因此机构的结构类型综合是机构学的重要研究内容[6].同样，对LEMs进行结构类型综合，不仅能够启发人们创新、发明新的LEMs，同时还可以对现有的机构进行优化，因此，对LEMs的结构类型综合就显得十分必要.自图论首次被应用到机构构型综合之后，机构构型综合便有了长足发展.文献[7]基于图论法综合得出16种8杆1自由度运动链.文献[8]采用Franke简明标记法，在一般情况下避免了同构问题，并且将其运用于9杆2自由度运动链的综合.文献[9]则采用缩图法首次综合出一共230种10杆1自由度运动链.文献[10]通过二副杆转化法得到839种11杆2自由度运动链.文献[11]建立了连杆拓扑图的规范表示法，并且提出了基于最大周长环路的同构识别方法.文献[12-13]运用有限对称群法计算出4～12杆、1～3自由度的运动链数目.文献[14]基于麦基型算法得到基本环路为1～6、自由度为1～4的运动链数目.文献[15-16]将Assur杆组作为邻接矩阵的基本元素，提出了杆组邻接矩阵的定义，并将其用于平面机构的综合，给出了一种机构综合的新方法，该方法的优势是能够同步辨识同构体，且在综合的过程中包含了主动件和机架变换的问题.文献[17]提出了一种自动创建连杆机构回路方程的算法，根据该算法，得出了71种8杆机构.文献[18-19]的研究提出了两种柔顺机构的综合方法：转换刚体综合和柔顺综合.其中转换刚体综合是将已知的刚体机构用柔顺机构替代，在替代过程中分两种情况：(1)直接用柔顺机构替代刚体机构；(2)先将复杂的刚体机构分解成相对简单的结构，然后再用相似的柔顺机构替代.

综上所述，目前对LEMs研究主要集中在运动副的实现上，同时各国学者对机构综合特别是平面机构综合提出了许多研究方法，但是在LEMs构型综合方面研究不足.针对上述研究现状，本文拟采用Assur杆组邻接矩阵法，进行平面连杆机构的结构类型综合，综合完成之后再将其转换成LEMs平面状态，以期丰富LEMs构型综合理论.

1　杆组分类

由机构的组成原理可知，机构是由一个或若干个自由度为零的运动链依次连接到主动件和机架上而组成的.这个自由度为零的运动链就称为杆组或Assur杆组.一般情况下，依据杆组中所含构件数目，可将杆组分为2杆组、4杆组以及6杆组[20]，如表1所示，杆组简图中实心圆表示杆组外副，空心圆表示内副.

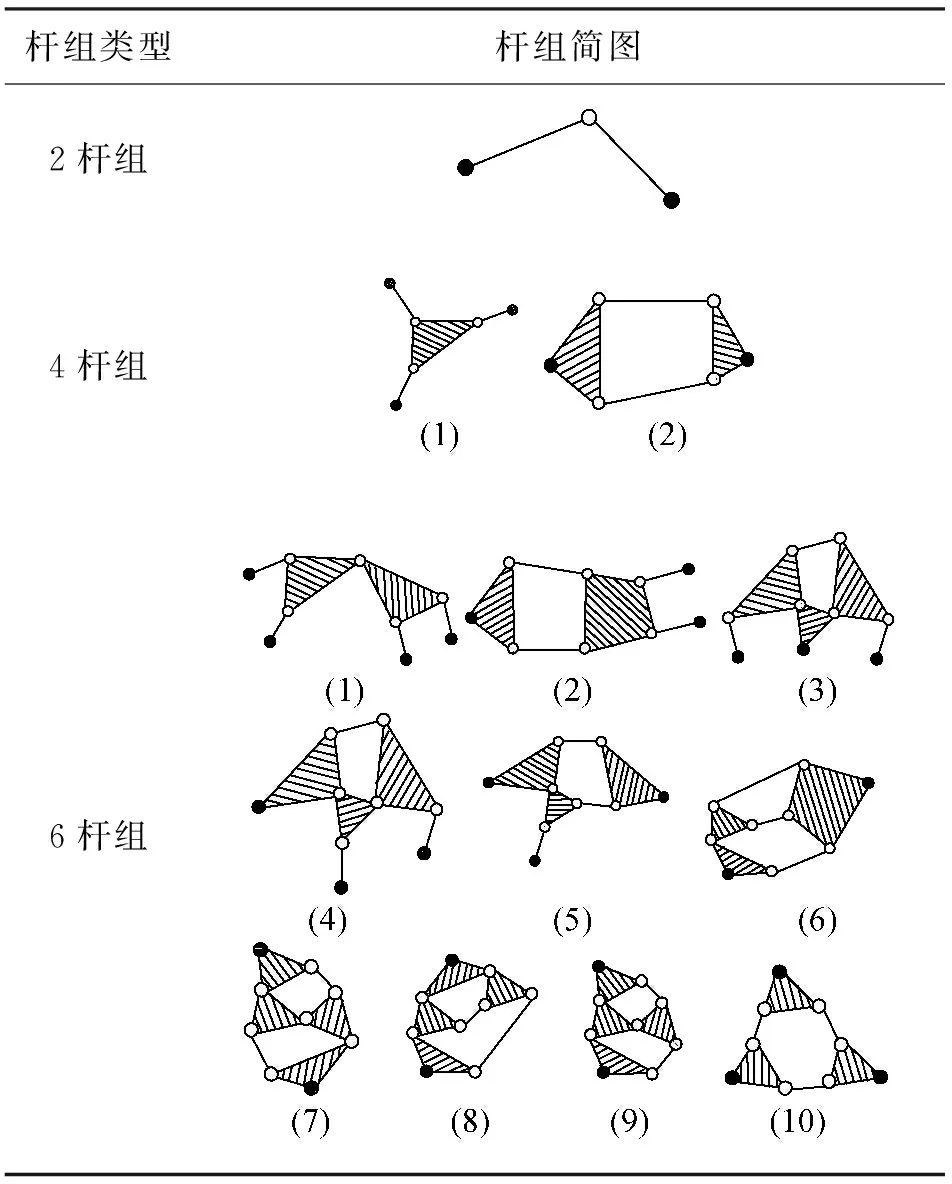
表1　各类型杆组Table 1　Different types of groups

2　杆组邻接矩阵

与传统邻接矩阵中以构件为基本元素不同，杆组邻接矩阵中基本元素为各Assur杆组，即：

(1)

3　LEMs构型综合研究

3.1总体综合过程

首先，依据机构总体构件数与各级杆组所含构件数的数学关系，分析基于1自由度8杆的所有杆组组合情况.其次，根据上述组合情况，搭建杆组邻接矩阵对角线元素，且同步辨识同构体.再次，将第一级以及之后的各杆组依据一定的约束条件依次连接到主动件、机架或前级杆组上，且同步辨识同构体，直至将全部杆组均连接完成，从而获得含单铰的1自由度8杆机构所有构型.最后，用相应的柔顺片段代替刚性片段，完成LEMs构型综合.

3.2杆组装配的约束条件

根据机构组成原理，将各级杆组依次连接到主动件、机架或前级杆组上，逐级构造杆组邻接矩阵，并且同步辨识同构体，最终获得所有构型.

当杆组依次装配到主动件和机架或者前级杆组时，要依据一定的约束条件：

(1) 杆组的外副必须全部连接到前级杆组或者主动件或者机架上；

(2) 杆组必须连接到运动已经确定的节点上；

(3) 不得将杆组的外副全部连接在同一构件(包括主动件与机架)上.

3.3杆组元素的装配连接组合

3.3.1单自由度机构构件数与杆组数关系

由于2杆组中构件数为2， 4杆组和6杆组中构件数分别为4和6，主动件和机架的构件数为1，所以平面机构的总构件数n与各杆组数之间的关系为

n-2=2nⅡ+4nⅣ+6nⅥ

(2)

式中：nc为各杆组的构件数(c=Ⅱ, Ⅳ, Ⅵ).

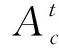
基于式(2)，以1自由度8杆机构为例，可由主动件、机架和3个2杆组，或1个2杆组加1个4杆组，或1个6杆组组成.由如下杆组邻接矩阵ATi(i=1, 2, …, 15)表示：

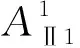
3.4主动件与机架的连接方式

默认主动件与机架相连，根据上述ATi(i=1, 2, …, 15)连接关系，在该节中，主动件与机架的连接关系可用如下邻接矩阵ADi(i=1, 2, …, 15)表示

3.5第一级杆组与主动件和机架的连接方式

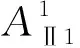
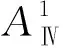
对由6杆组组成的机构，当第一级杆组连接到主动件和机架时，就完成了构型综合，现讨论如下.

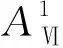
3.6第二级杆组与前各元素之间的连接方式

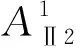
由AG2开始综合，可以得到如下连接方式：

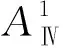
由AG3开始综合，可以得到如下连接方式：

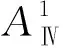
辨识同构体：将AF31与AF7中m=01且j=02的构型相对比发现，其各自的2杆组和4杆组分别连接到各自的主动件和机架上，区别仅是连接顺序不同，最终结果相同，故为同构体，因此删除AF31.在这一节中共有10种不同连接方式.

由AG4开始综合，可以得到如下连接方式：

上述连接情况与上一节中类似，AF41与AF7中m=02且j=01的构型为同构体，故删除AF41.在这一节中共有10种不同连接方式.

由AG5开始综合，可以得到如下连接方式：

此节中由AG5出发综合所得共6种不同构型.

由AG6开始综合，可以得到如下连接方式：

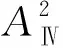
辨识同构体：

AF57=AF41

由对比可知，AF57与AF41仅仅是连接顺序不同，最终结果相同，因此为同构体.在这一节中由AG6出发综合所得共10种不同连接方式.

3.7第三级杆组与前各元素之间的连接方式

开始综合由3个2杆组组成的8杆机构中最后一个2杆组所有的连接方式.

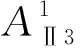
理论上向量Ti一共有以下14种可能：

上述向量中的q均能取2个值，因此T2, T4, T8, T10均有2种不同的连接方式.在T12中，在前面2个2杆组中各取1个构件相连，去除1种重复情况，因此T12有3种不同连接方式.

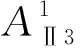
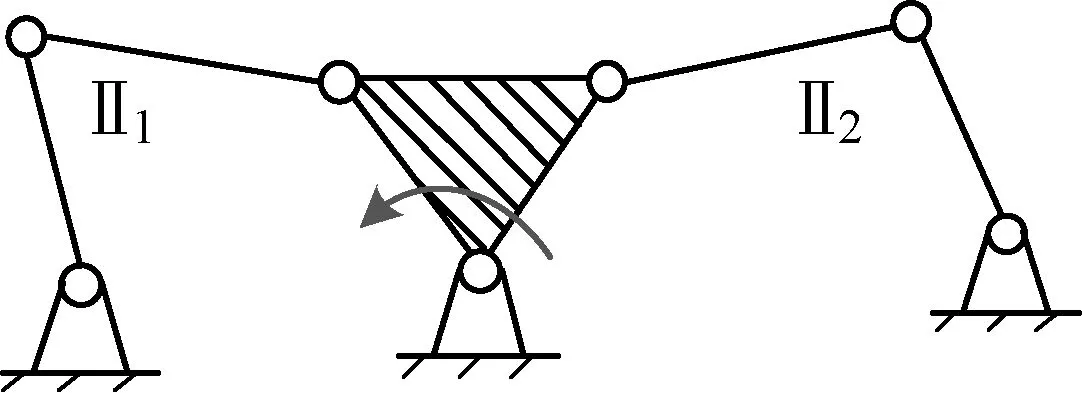
图2　AF1未连上最后1个2杆组时的构型Fig.2　The configuration that AF1haven’t connected the last groupⅡ

同理可得，由AF2至AF6综合所得的不同连接方式分别有14, 13, 12, 11, 10种.

综上所述，由3个2杆组组成的1自由度8杆机构共有9+14+13+12+11+10=69种构型，由1个2杆组和1个4杆组组成1自由度8杆机构一共有14+10+10+6+10=50种构型，由1个6杆组组成的1自由度8杆机构共有30种构型.因此，包含机架和主动件变换的1自由度8杆机构共有149种不同构型.

3.8LEMs构型综合

由上述步骤所得1自由度8杆单包含主动件和机架变换问题的机构共149种，基于目前常用的LEMs转动副，采用相应柔顺片段替代综合所得的构型，转化为LEMs平面状态，完成LEMs构型综合.以其中一种为例，结果如图3和4所示.

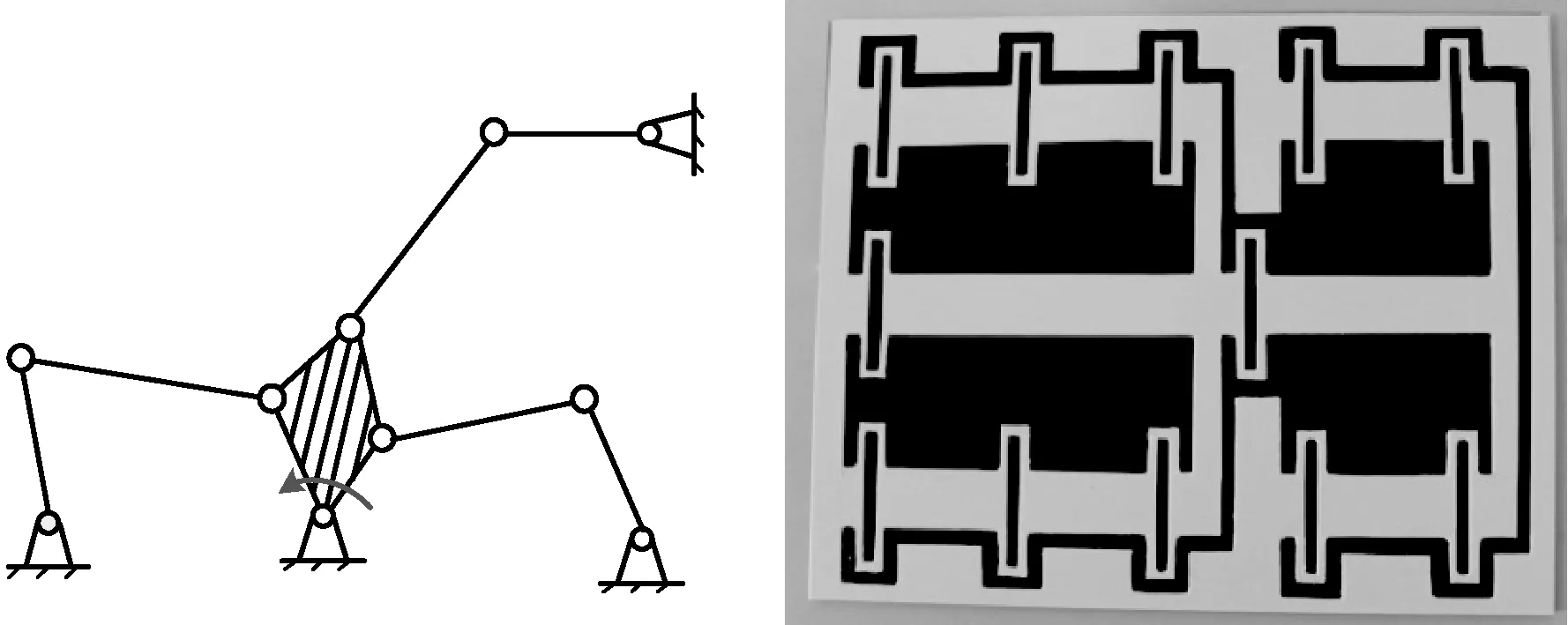
图3　平面8杆机构及处于平面状态的8杆LEMsFig.3　Structure of an eight-bar mechanism and its LEMs in planar

图4　8杆LEMs的CAD模型及处于浮出状态的8杆LEMsFig.4　CAD model of an eight-bar LEMs and its emergent state

4　结　语

本文采用平面机构综合问题的方法来研究LEMs构型综合问题.基于杆组邻接矩阵，以8杆机构为例，对构型综合问题进行研究，最终得到包含主动件和机架变换的149种全铰链平面8杆机构.选取其中一种平面8杆机构，采用相应柔顺片段替代综合所得的构型，将其转换成LEMs平面状态，并得到其CAD模型及实体模型.本文所述综合过程仅含有单自由度单铰运动链，多自由度含复合铰链的LEMs构型综合是今后的研究方向.

[1] JACOBSEN J O, WINDER B G, HOWELL L L, et al. Lamina emergent mechanisms and their basic elements [J]. Journal of Mechanisms and Robotics, 2010, 2(1):1-9.

[2] JACOBSEN J O, CHEN G M, HOWELL L L, et al. Lamina emergent torsional (LET) joint [J].Mechanism and Machine Theory, 2009, 44(11): 2098-2109.

[3] FERRELL D B, ISAAC Y F, MAGLEBY S P, et al. Development of criteria for lamina emergent mechanism flexures with specific application to metals [J]. Journal of Mechanical Design, 2011, 133(3): 031009-031009-9.

[4] WILDING S E, HOWELL L L, MAGLEBY S P. Introduction of planar compliant joints designed for combined bending and axial loading conditions in lamina emergent mechanisms [J]. Mechanism and Machine Theory, 2012, 56(11): 1-15.

[5] 邱丽芳，楚红岩，杨德斌，等.基于伪刚体模型的多层LEMs建模与仿真[J].农业机械学报，2013，44(9)：255-260.

[6] 曹惟庆.连杆机构的分析与综合[M].2版.北京：科学出版社，2002.

[7] FREUDENSTEIN F, DOBRJANSKYJ L. On a theory for the type synthesis of mechanisms [J]. Applied Mechanics, 1964(1):420-428.

[8] DAVIES T H, CROSSLEY F E. Structural analysis of plane linkage by Franke’s condensed notation [J]. J Mechanisms, 1966(1):171-184.

[9] WOO L S. Type synthesis of the plane linkages [J]. Journal of Manufacturing Science and Engineering, 1967, 89(1): 152-172.

[10] MRUTHYUNJAYA T S. Structural synthesis by transforma-tion of binary chains [J]. Mechanism and Machine Theory, 1979, 14(4): 221-231.

[11] DING H, HUANG Z. The establishment of the canonical perimeter topological graph of kinematic chains and isomorphism identification [J]. ASME Journal of Mechanical Design, 2007, 129(9): 915-923

[12] TUTTLE E R, PETERSON S W, TITUS J E. Enumeration of basic kinematic chains using the theory of finite groups [J]. Journal of Mechanical Design, 1989, 11(1): 498-503.

[13] TUTTLE E R. Generation of planar kinematic chains [J]. Mech Mach Theory, 1996, 31(4): 729-748.

[14] SUNKARI R P, SCHMIDT L C. Structural synthesis of planar kinematic chains by adapting a Mckay-type algorithm [J]. Mechanism and Machine Theory, 2006, 41(9):1021-1030.

[15] 李树军，戴建生.基于Assur杆组元素的平面机构的拓扑描述[J].机械工程学报，2011，47(19)：8-14.

[16] 李树军，戴建生.基于杆组邻接矩阵的平面机构综合方法[J].机械工程学报，2012，48(13)：13-18.

[17] PARRISH B E, MCCARTHY J M, EPPSTEIN D. Automated generation of linkage loop equations for planar 1-dof linkages, demonstrated up to 8-bar[C]// Proceedings of the 2014 ASME International Design Engineering Technical Conference & Computers and Information in Engineering Conference, 2014.

[18] BERGLUND M D, MAGLEBY S P, HOWELL L L. Design rules for selecting and designing complain mechanism for rigid-body replacement synthesis[C]//Proceedings of the 2000 ASME International Design Engineering Technical Conference， 2000.

[19] HOWELL L L．柔顺机构学[M]．余跃庆，译．北京：高等教育出版社，2007．

[20] 熊滨生.现代连杆机构设计[M].北京：化学工业出版社，2005.

Research for Single Joint LEMs Types with One Degree of Freedom and Eight Bars

WANGQiang1,CAOYi1, 2, 3, 4,CHENGui-lan1

(1. School of Mechanical Engineering, Jiangnan University, Wuxi 214122, China;

2. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiaotong University, Shanghai 200240, China ;

3. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150080, China;

4. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Wuxi 214122, China)

A structural synthesis method of Lamina Emergent Mechanisms (LEMs) with revolute joint is proposed, which can apply to the research for single joint LEMs types of one degree of freedom and eight bars with the frame and driver link transformation. First, the LEMs in the plane can be equivalent to the planar kinematic chains, and the group-based adjacent matrix of the planar kinematic chains is constructed to solve all possible connection types of planar mechanism which are given the number of bars and degree of freedom. Then, according to the number of bars and degree of freedom, analysis all the combination of Assur groups, in order to set up the frame of the group-based adjacent matrix, the first stage and later groups are assembled to the driver link and frame or former groups. The isomorphism is identified in synchronism, and the connections of planar mechanism with only revolute pair are obtained. Finally, the obtained planar kinematic chains are restored to LEMs in the planar.

lamina emergent mechanisms(LEMs); structural synthesis; adjacent matrix

1671-0444(2015)06-0795-07

2014-10-20

国家自然科学基金资助项目(50905075)；教育部中央高校基本科研业务专项基金重点项目资助项目(JUSRP51316B)；机械系统与振动国家重点实验室开放课题资助项目(MSV201407)；机器人技术与系统国家重点实验室开放基金资助项目(SKLRS-2012-MS-07)；江苏省高校“青蓝工程”优秀青年骨干教师人才基金资助项目；江苏省食品先进制造装备技术重点实验室开放课题资助项目(FM-201402)；江苏省普通高校学术学位研究生科研创新计划项目资助项目(KYLX-1115)

王强(1989—)，男，浙江嘉兴人，硕士研究生，研究方向为机器人机构学和柔顺机构. E-mail: jewelzor@163.com

曹毅(联系人)，男，副教授， E-mail: caoyi@jiangnan.edu.cn

TH 122

A