基于模糊理论的双车道公路线形安全评价

季新年，樊　军，陈一飞

基于模糊理论的双车道公路线形安全评价

季新年1，樊军2，陈一飞2

（1.江苏省交通运输厅工程质量监督局，江苏南京 210001；2.解放军理工大学，江苏南京 210007）

双车道公路由于建设投资、地形地貌等诸多因素限制，在进行公路线形设计时常采用规范规定的极限指标，存在一定的安全隐患，实际运营中交通事故率较高。文章以模糊数学理论为指导，建立双车道公路的几何线形安全评价体系，确定安全评价打分标准，建立相关隶属函数，对各安全评价指标赋权，最终评价双车道公路整体线形的安全等级以提出针对性的工程改善对策。

双车道公路；模糊理论；线形设计；安全评价

近年来我国公路通车里程持续增长，机动车数量大幅增加，公路交通事故频发，道路交通安全已成为比较严重的社会问题。截至2013年底，二、三级公路里程约占我国等级公路里程的20%，而交通事故数量、受伤人数、死亡人数在道路交通事故总数中占比较高［1］。一个重要的因素是在初期建造时公路的几何线形设计采用了较多极限技术指标，尤其山区双车道公路不少是以设计车速为依据，导致线形设计存在较多安全隐患。本文采用模糊评价理论，对某山区双车道公路在改建之前进行了线形安全性评价。

该山区双车道公路全线按二级公路标准设计，改建路段全长26 km，选取其中约5 km （K1+000～K5+863.275）的路段进行安全评价。评价路段共有平面交点10个，其中平曲线最小半径为130.00 m，位于JD13（K4+138.417）处，且此处无竖曲线，选取此路段为评价对象。

1　评价体系建立

双车道公路在平面、纵断面线形方面由于受到投资限制，较多地随地形走势布线，因此线形安全评价的重点是平面和纵断面线形指标，同时考虑驾驶员实际驾驶安全和舒适方面的需求，筛选出主要的评价指标。建立公路线形安全评价3层结构体系，一级指标包括速度、线形、舒适性、连续性、弯道密度；速度指标考虑两方面的差异性，即设计速度与运行速度的差异，相邻路段运行速度的差异；线形指标考虑离散程度，即平曲线半径与平均半径的偏离度，纵断面竖曲线曲率与平均曲率的偏离度。具体指标如图1所示。

图1　公路线形安全性评价指标体系

设计速度与运行速度差值Δv按下式计算：

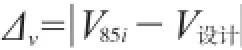
式中：V85i为评价路段上第85位百分点的车辆行驶速度（简称运行速度），本文中运行速度根据《公路项目安全性评价指南》［2］（以下简称《指南》）确定。

相邻路段运行速度比值RV按下式计算：

式中：V85i，V85i-1分别为当前路段和前一路段第85位百分点的运行速度。

单曲线半径与平均半径之比KR按下式计算：

式中：R设计值为评价圆曲线的半径R设计值；Ri，Li分别为第i个圆曲线的半径和长度。

单竖曲线率与平均竖曲线率之比Kv按下式计算：

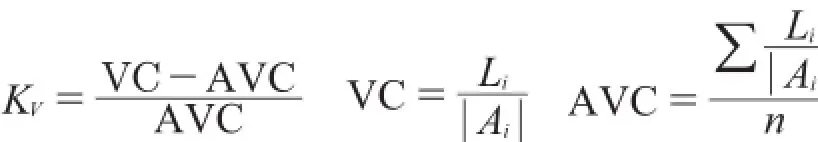
式中：Li为路段上第i个竖曲线长度；Ai为路段上第i个竖曲线上坡度代数差的绝对值；n为路段竖曲线的个数。

舒适性指标ah按下式计算：

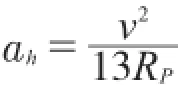
式中：RP为评价圆曲线上某点的曲率半径；v为圆曲线上的运行速度。

总体线形连续性评价指标C按下式计算：

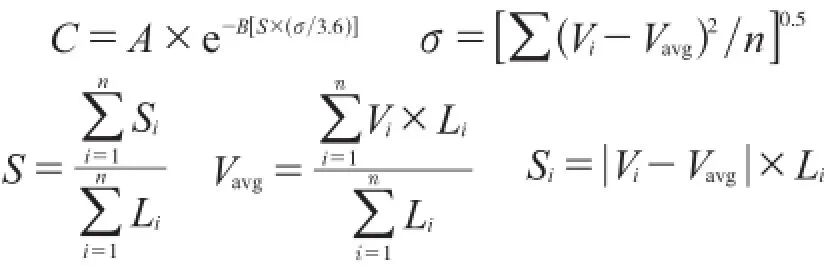
式中：Li，Vi分别为评价第i个路段所对应的长度和运行速度；Vavg为平均运行速度；A为回归参数；n为路段数。

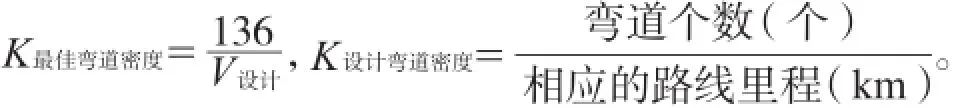
2　单因素评判

参考相关文献［3-4］，依据评判标准（由各单因素直接计算值查表1确定对应的评价等级，根据表2内插得到对应的百分制得分）确定路线各指标的得分值，见表3。

表1　公路线形安全指标评判表

表2　公路几何线形安全评价指标分值区间

表3　路线各指标得分值

3　计算隶属度

模糊关系矩阵R（［rij］）是因素论域u=｛Δv，RV， KR，Kv，ah，C，KD｝到评语等级论域V=｛优，良，差｝的模糊子集，其中rij是第i个评判因素ui属于第j个评语等级的程度［5］。

为了反映双车道公路几何线形安全指标值的优劣性，采用隶属度描述各指标属于某种评语的模糊程度，隶属度由以下隶属函数式决定。

由此，根据表2计算得分和隶属函数式得出各指标的隶属度，并将其归一化可得：

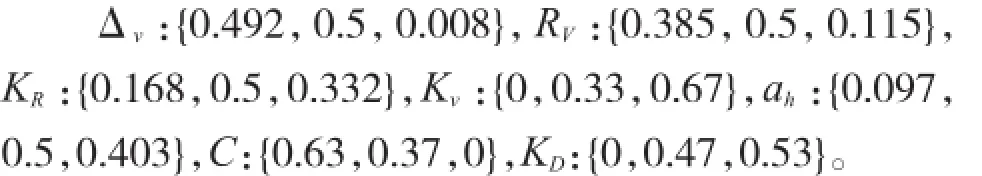
4　模糊综合评价

确定不同指标的权重向量W，采用层次分析法来确定双车道公路几何线形安全评价一级指标的权重，采用主客观组合赋权法确定其二级指标的权重。通过计算分析，得出线形安全评价体系中一级指标的判断矩阵和二级指标的权重分别如表4和表5所示。

表4　一级指标判断矩阵

表5　二级指标的权重

采用由综合二级指标评价得到一级指标，再综合一级指标的评价结果得到线形安全性的总体评价结果，以优、良、差3个等级表示。

根据确定的二级指标权重系数，按照模糊关系式可得速度指标B1的隶属度为：

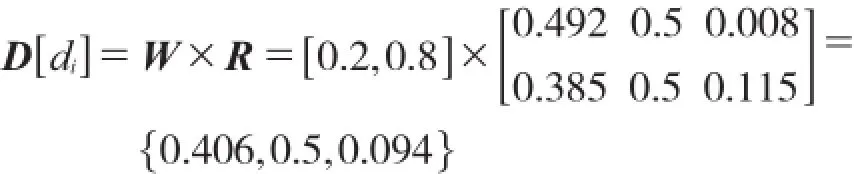
线形指标B2的隶属度为｛0.072，0.403，0.525｝；舒适性指标B3、连续性指标B4、弯道密度指标B5的隶属度分别为｛0.097，0.5，0.403｝、｛0.63，0.37，0｝、｛0，0.47，0.53｝。

根据确定的一级指标权重系数及模糊关系式，得出评价道路的几何线形总体安全性模糊综合评价结果为：

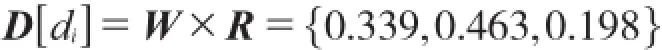
按照最大隶属度原则，由以上模糊综合评价结果可知，该山区双车道公路的安全评价等级为“良”。计算得到的线形安全指数为：ASI = 90×0.339 +70× 0.463 + 50×0.198=72.82。

从得到的线形安全指数可以看出，该山区双车道公路的总体安全状况较好，但是在一些具体的指标如ah、Kv、KD，即舒适性、连续性、弯道密度等方面，评价结果并不理想。可以针对平曲线曲率、交点数量等，相应地采取一些改造工程措施，如将JD13位置利用弯道内侧平台拓宽增大平曲线半径，K2+130处削坡降低纵断面坡度等［6］，从而提高公路整体交通运营安全水平。

5　结语

采用模糊数学理论方法，对影响山区双车道公路路线安全的多因素进行综合考虑，得到整体的评价结果和各指标评价结果。对改建工程的几何线形方案进行安全性评价，提出针对性的工程改善措施，为提高双车道公路安全水平提供理论参考。

［1］交通运输部.2013年交通运输行业发展统计公报［R］.2014.

［2］JTG/T B05—2004公路项目安全性评价指南［S］.

［3］李建士.路线安全设计方法的研究与应用［D］.西安：长安大学，2004.

［4］李志宏.双车道公路线形安全性研究［D］.上海：同济大学，2009.

［5］杨纶标，高英仪.模糊数学原理及应用［M］.广州：华南理工大学出版社，2005.

［6］郭忠印，方守恩.道路安全工程［M］.北京：人民交通出版社，2003.

Alignment Safety Evaluation for Double-Lane Highway Based on Fuzzy Theory

Ji Xinnian1， Fan Jun2， Chen Yifei2
（1. Quality Supervision Bureau of Transportation Department of Jiangsu Province， Nanjing 210001， China；2. PLA University of Science and Technology， Nanjing 210007， China）

Due to limits of the investment， terrain and many other restrictions， limit indicators are often used in the double-lane highway alignment design， which causes more safety problems and higher accident rates. Based on Fuzzy theory， a alignment safety evaluation system for double-lane highway is established to determine the scoring criteria， the membership function of each index empowerment is established， the final evaluation of the safety level of the overall alignment is got， evaluation results could be taken as reference for engineering improvement.

double-lane highway； Fuzzy theory； alignment design； safety evaluation

U491.21

A

1672-9889（2015）01-0051-03

季新年（1967-），男，江苏兴化人，工程师，主要从事公路水运工程质量监督和安全监管工作。

（2014-06-03）