宽带宽测绘带SAS非线性线频调变标算法

田振，唐劲松，钟何平，张森

(海军工程大学海军水声技术研究所，湖北武汉430033)

合成孔径声呐［1-2］(synthetic aperture sonar，SAS)是一种新型体制的水下成像声呐，因其同时具有较高的距离分辨力和方位分辨力，在军事、民用以及海洋研究领域得到了重要应用。由于高频声信号在水下衰减较快，为提高探测距离，不可避免地需要采用低频声信号。SAS的工作频率一般为几十至几百千赫兹，要实现距离向的高分辨成像则需要提高信号带宽［3-4］。由于SAS系统的带宽载频比不断降低，现有以窄带近似为基础的大多数成像算法不再适用［5］。另外，提高测绘带宽以提高测绘速率也是目前SAS成像算法亟需解决的问题之一。因此，设计实现能够满足宽带宽测绘带成像需求的SAS成像算法具有十分重要的意义。

线频调变标(chirp-scaling，CS)算法［6］不需要耗时的插值运算且具有相位保真度高的优点，一直被广泛应用于各种场景的 SAS/SAR成像［7-12］。为此，Nieves［13］和 Potsis［14］分析了 CS 算法应用于宽带 SAS成像的可行性。文献［15］认为可以通过适当改进非线性CS(nonlinear CS，NCS)算法实现超宽带SAR成像。文献［16］指出适用于大斜视SAR成像的NCS算法往往也适用于具有大带宽发射信号的SAS成像，并提出了一种适用于宽带SAS成像的改进NCS算法。由于该算法在推导由三次和四次相位滤波及NCS操作引入的相关变量时，没有考虑距离频率高阶项中等效调频斜率随时延差量的二阶变化特性，导致测绘带边缘模糊，降低了有效测绘带宽。

针对这个问题，本文在文献［16］中改进的NCS算法的基础上，继续对算法进行改进，特别是在推导由三次和四次相位滤波及NCS操作引入的相关变量时，充分考虑距离频率高阶项中等效调频斜率随时延差量的二阶变化特性，有效解决了改进的NCS算法中测绘带边缘点的散焦问题，大大增加了有效测绘带宽。本文最后进行了仿真分析，并与传统的NCS算法和改进的NCS算法的成像结果进行了对比。

1 信号模型

在SAS系统中，目标的回波是在距离向和方位向扩散开来的，可以将SAS回波信号的接收看作从目标空间到信号空间的映射，而成像过程则是从信号空间到图像空间的映射。假定SAS发射和接收信号的过程中，满足停走停近似。SAS通常发射线性调频信号，为方便计算，本文取成像区域内固定点目标 (r，0)进行分析。在t时刻，假定声基阵坐标为 (0，vt)，v表示SAS平台航速。此时，点目标响应的斜距历程可以表示为经过调制解调，点目标回波响应可以表示为

式中:A0为常数，ωr(·)由发射信号复包络形状决定，ωa(·)由声基阵的指向性函数决定，τ为距离向快变时间，μ为信号的调频斜率，f0为信号载频，c为水下声速。

2 扩展的NCS算法推导

NCS算法通常在二维频域或者距离多普勒域进行，忽略幅值对成像的影响，将R(t;r)的表达式代入式(1)，并通过二维傅立叶变换(Fourier transform，FT)将信号转换到二维频域，可得点目标响应二维谱为

式中:Wr(·)表示距离向的信号包络，Wa(·)表示方位向的信号包络，fr表示距离向瞬时频率，fa表示方位向瞬时频率。不妨令

对fr进行泰勒级数展开，可得

其中前四阶系数项为

2.1 二维谱高阶项补偿

分析式(3)可以发现，宽带成像和窄带成像的区别在于式(4)泰勒级数展开时保留的阶数。窄带成像时，fr≪f0成立，忽略高阶项是允许的;宽带成像时，fr≪f0不再成立，高阶项带来的相位误差较大，因而不能忽略。对于宽带成像，可以通过与一个参考距离rref处的相位因子相乘近似补偿高阶项引入的相位误差，该相位因子表达式为

2.2 三次和四次相位滤波

传统的 NCS 算法［8］在对 φ(fr，fa;r)进行泰勒级数展开时仅考虑fr的三阶项，由于本文考虑fr的四阶项，故需要引入三次和四次相位滤波函数:

式中:Y(fa)和Zm(fa)为待求量。三次和四次相位滤波之后，点目标响应二维谱相位变化为

这里近似认为在成像区域内φ4(fa;r)是距离空不变的，并用φ4(fa;rref)替代。注意，传统NCS算法并没有考虑四阶项，且认为φ3(fa;r)是距离空不变的，而本文则充分考虑φ3(fa;r)的距离空变性。此时，将回波响应通过距离向逆FT(inverse FT，IFT)回到距离多普勒域，其距离多普勒谱相位为

式中:τ0=2r/c表示不同距离处的时延，ks(fa;τ0)=1/[ μ-1－ksrc]表示信号的等效调频斜率，A(fa)=

2.3 NCS操作

与传统的NCS算法不同，改进的NCS算法考虑了等效调频斜率随时延差量的一阶线性变化和二阶非线性变化特性，即

其中，Δk1(fa;τref)和 Δk2(fa;τref)为ks(fa;τ0)在参考距离处随时延差量的一阶和二阶变化率，其表达式由ks(fa;τ0)的泰勒展开系数确定，即

式中:Δksrc(fa)=(D-3－D-1)/f0，τref=2rref/c表示参考距离处的时延。

NCS操作在距离多普勒域进行，主要校正不同距离处的距离徙动差量，使不同距离处的信号具有一致的距离徙动量，操作函数为

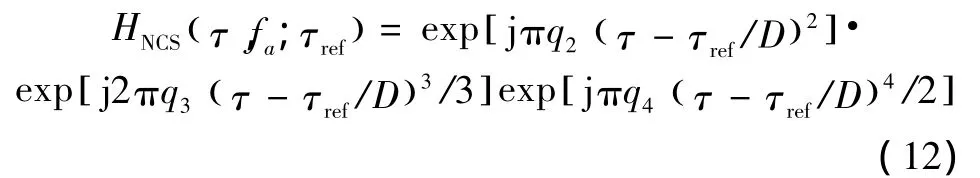
式中:q2、q3和q4分别是q2(fa;τref)、q3(fa;τref)和q4(fa;τref)的简写形式，为待求参量。将回波信号与式(12)相乘完成NCS操作，然后通过距离向FT将回波响应变换到二维频域，可得

注意，这里在进行距离向FT时，仍然假设驻定相位点与τ的三次以上项无关。为简化公式，不妨将Y(fa)、和Δksrc(fa)简写为Y、Z、Δτ、ks、ksr、A和 Δksrc。考虑到Aτ0=AΔτ+Aτref，经过整理，式(14)中各相位项可以分别表示为

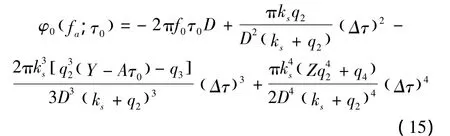
式(15)为方位压缩项以及三次和四次相位滤波及NCS操作引入的剩余相位项，该项可以在方位向IFT前通过相位相乘予以补偿。

式(16)对应于点目标距离向坐标和距离向走动项，因此需要保留关于Δτ的常数项和一次项。将式(9)代入式(16)并展开成Δτ的函数，且保留至Δτ的三阶项。令展开式中Δτ的二次项及三次项系数为0，这样就消除了距离向走动的空变现象。需要注意的是，这里充分考虑式(9)中Δτ的二阶项，而文献［16］仅部分考虑了Δτ的二阶项，这会导致一定的误差。

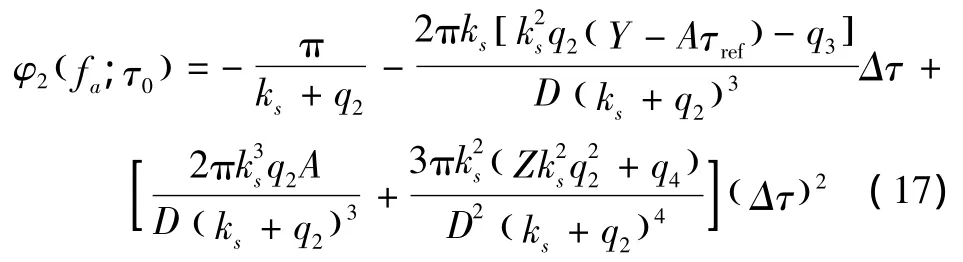
式(17)对应于二次距离压缩项，仅需保留常数项即可。将式(9)代入式(17)并展开成Δτ的函数，仅保留至Δτ的二阶。令展开式中Δτ的一次项及二次项系数为0，这样就消除了二次距离压缩的线性和二阶非线性变化项。同样的，文献［16］仍部分考虑了Δτ的二阶项，从而引起一定的误差。

式(18)对应于fr的三阶耦合项，因此保留常数项即可。将式(9)代入式(18)并展开成Δτ的函数，仅保留至Δτ的一阶。因此，令展开式中Δτ的一次项系数为0即可消除三阶耦合量的空变特性。

式(19)为四次相位滤波及NCS操作引入的剩余相位项。这里近似认为φ4(fa;τ0)是距离空不变的，即φ4(fa;τ0)≈φ4(fa;τref)。该项通常在二维频域通过相位相乘进行补偿。联立式(16)～(18)可以解得待定系数q2、q3、q4、Y、Z的表达式分别为

2.4 距离压缩、SRC与RCMC

NCS操作后，点目标响应二维谱相位变化为

NCS算法一般在二维频域通过相位相乘完成距离压缩、二次距离压缩(secondary range compression，SRC)与距离徙动校正(range cell migration correction，RCMC)处理，其参考因子为

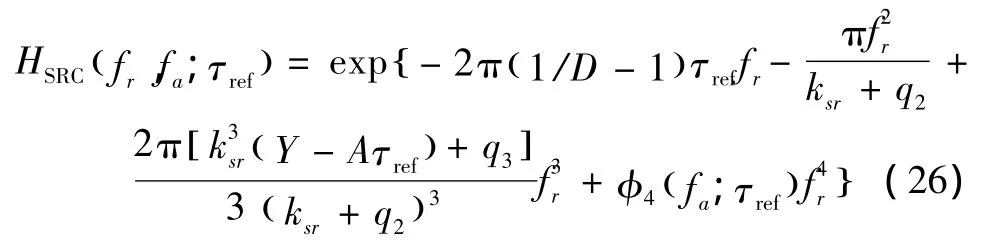
2.5 方位压缩、方位走动校正与剩余相位补偿

方位压缩、方位走动校正与剩余相位补偿一般在距离多普勒域进行。距离向压缩及RCMC以后，通过距离向IFT进入距离多普勒域，方位压缩、方位走动校正与剩余相位补偿因子为

最后，通过方位向IFT回到距离时域、方位时域，算法推导结束，流程图如图1所示。

图1 本文算法流程图Fig.1 Block diagram of the proposed algorithm

3 测绘带宽的影响因素分析

上述扩展的NCS算法推导过程中主要的近似处理有2项:第1项是泰勒级数展开近似至四阶，四阶以上高阶项用参考距离处的补偿因子予以补偿;第2项是仅考虑等效调频斜率随Δτ的一阶线性和二阶非线性变化特性，忽略其高阶特性。由于这两项操作会带来一定的相位误差，若要使得该部分相位误差低于π/8，测绘带宽必然会受到一定影响，下面分别进行具体分析。

3.1 泰勒级数展开近似对测绘带宽的影响

对φ(fr，fa;r)进行泰勒级数展开并保留低阶项的前提条件是要求下式成立:

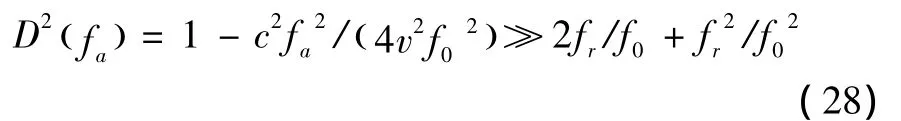
该式表明带宽载频比越小、方位波束越窄，成像结果越精确。对于宽带系统而言，fr≪f0不再成立，仅保留与fr相关的低阶项会导致泰勒级数近似的近似性变差，因此宽带条件下需要保留更高阶次项以减小泰勒近似带来的相位误差。该文对φ(fr，fa;r)进行泰勒级数展开并保留至四阶，并用参考距离处的高阶相位项补偿四阶以上项高阶相位，以便降低宽带条件下泰勒近似带来的相位误差。该操作引入的相位误差可以表示为

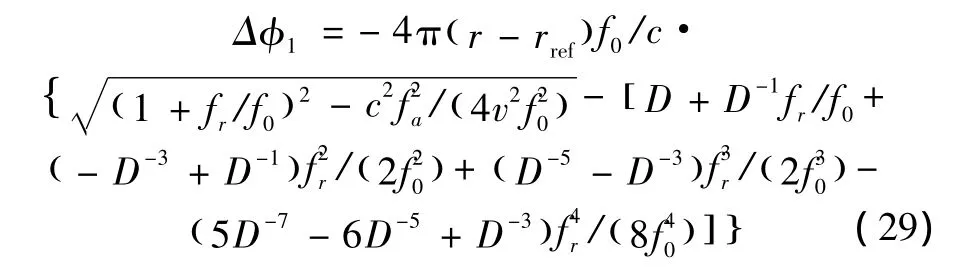
用ΔRswath表示测绘带宽度，即有

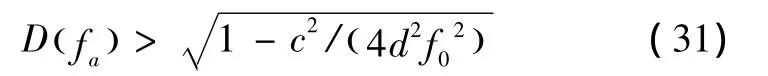
图2绘制了ΔRswath随Br和f0的变化规律，仿真过程中取d=0.08 m，c=1 500 m/s。其中，图2(a)绘制了ΔRswath随Br和f0的二维变化情况，图2(b)～(d)绘制了3种不同信号带宽情况下，ΔRswath随f0的变化情况。单独看图2(b)～(d)可以发现，当Br固定时，ΔRswath随着f0的增大而增大。纵向比较图2(b)～(d)可以发现，f0不变时，ΔRswath随着Br的增大而急剧减小。也就是说，ΔRswath与Br/f0成反比。这恰好说明了窄带条件下泰勒级数展开并保留低阶项对测绘带宽影响不大，宽带条件下应用泰勒级数展开近似时必须保留更高阶项，以防止测绘带宽的急剧下降。

图2 ΔRswath随Br及f0的变化规律Fig.2 ΔRswathvarying with Brand f0

3.2 等效调频斜率近似对测绘带宽的影响

由式(9)可知，等效调频斜率被近似至时延差量的二阶项，该近似引起的误差可以表示为

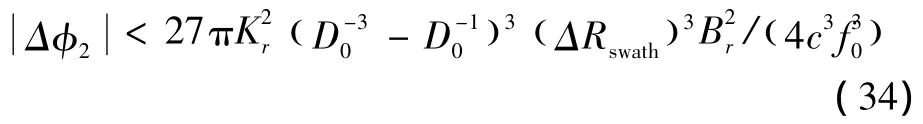
令式(34)等式右侧为 Δφ'2，若 Δφ'2＜π/8，那么必然成立，此时测绘带宽取值范围为

图3绘制了传统NCS算法［8］和本文的扩展NCS算法的等效调频斜率近似导致的ΔRswath随Br及f0的变化关系，仿真过程中取d=0.08 m，c=1 500 m/s，Tr=20 ms，其中Tr表示信号脉宽。另外，信号调频斜率可以通过公式Kr=Br/Tr求得。其中，图3(a)绘制了传统NCS算法中等效调频斜率近似导致的ΔRswath随信号载频f0及带宽Br的变化关系，图3(b)绘制了本文扩展NCS算法中等效调频斜率近似导致的ΔRswath随信号载频f0及带宽Br的变化关系。观测图3可以发现，随着带宽频率比的不断提高，有效测绘带宽急剧下降，这表明适应于窄带条件的有效测绘带宽并不一定适应于宽带条件。

图3 不同算法中ΔRswath随Br及f0的变化规律Fig.3 ΔRswafthvarying with Brand f0in different algorithms

当中心频率为100 kHz时，表1绘制了不同带宽时的有效测绘带宽。从表1可以发现，当带宽分别为20、40、60 kHz时，传统NCS算法的有效测绘带宽分别为421.70、149.10、81.15 m，而本文扩展的 NCS 算法可以分别达到 763.1、302.8、176.4 m。对比之后可以发现，无论是窄带条件还是宽带条件，本文扩展的NCS算法均具有比传统的NCS算法更宽的有效测绘带宽。

表1 不同Br时的有效测绘带宽Table 1 Mapping swath in different Br m

3.3 分析与讨论

通过上述分析可以发现以下2点结论:1)窄带条件下，泰勒级数展开近似并保留二阶项对有效测绘带宽几乎没有影响，但在宽带条件下，必须保留更高阶项以避免有效测绘带宽的急剧下降;2)等效调频斜率通常通过泰勒级数展开成时延或距离差量的函数，保留的阶数越高，对有效测绘带宽的影响越小。本文扩展的NCS算法正是在此基础上提出的，从而与传统NCS算法相比具有更好的宽测绘带适应性。另外，上述2种近似均对测绘带宽有影响，在实际应用时需要综合考虑。

4 仿真试验

为了验证扩展的NCS算法的有效性，本节分别利用传统的 NCS算法［8］、改进的 NCS算法［16］以及本文算法对成像场景参考点(100 m，0 m)及边缘点(60 m，0 m)处的点目标仿真数据进行处理，仿真参数如表2所示。假设成像场景的测绘带中心与SAS航线之间的垂直距离为100 m。为考察不同成像算法的成像指标，仿真过程中，距离向和方位向处理均不进行任何加权，且以测绘带中心位置为参考距离。需要注意的是，此时的带宽载频比达到66.67%，能够满足SAS成像的宽带条件。

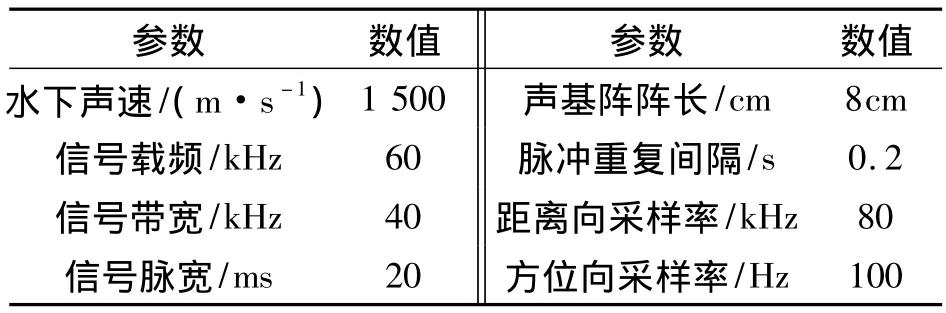
表2 仿真参数Table 2 Simulation parameters

图4(a)～(c)分别绘制了利用传统NCS算法、改进的NCS算法和本文算法对参考点(100 m，0 m)处点目标数据进行处理得到的结果，其中横坐标表示距离向，纵坐标表示方位向。对比发现，3种算法均能实现参考点(100 m，0 m)处点目标的良好聚焦。

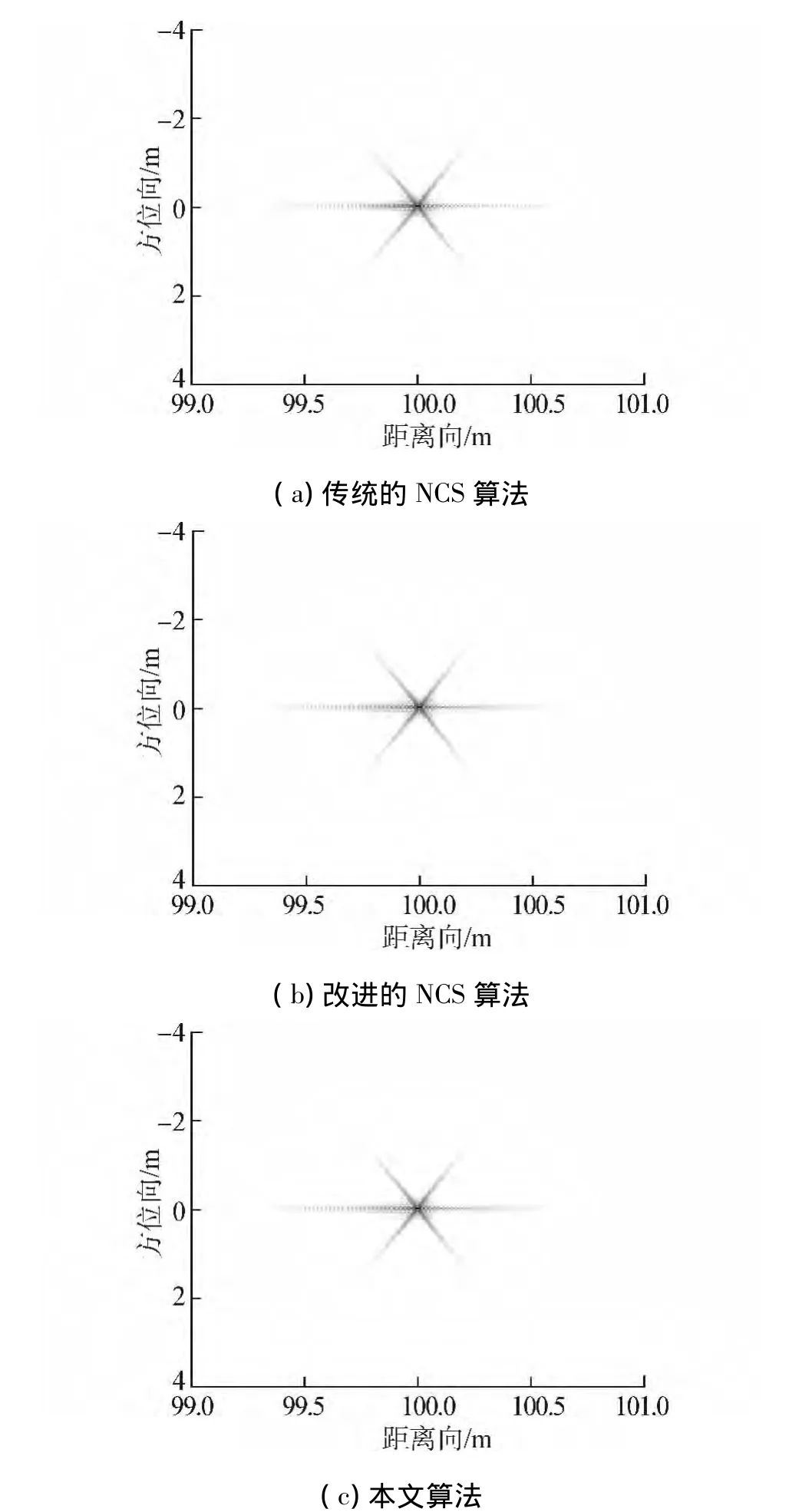
图4 参考点(100 m，0 m)处点目标成像结果Fig.4 Imaging result of the reference point target located at(100 m，0 m)

图5绘制了3种算法对边缘点(60 m，0 m)处点目标数据进行处理得到的结果。随着测绘带宽的增大，传统NCS算法和改进的NCS算法均出现较为明显的散焦现象，分别如图5(a)和5(b)所示。前者散焦的原因在于仅考虑fr二阶项的距离空变性，且认为三阶及三阶以上项是距离空不变的。另外，也与该算法中等效调频斜率近似时仅考虑时延差量的一阶项有关。后者散焦的原因在于其推导由三次和四次相位滤波以及NCS操作引入的相关变量时，仅部分考虑了等效调频斜率随时延差量的二阶项。由于本文算法并不存在这些近似，故而获得了较好的成像效果，如图5(c)所示。纵向比较图4(c)和5(c)可以发现，测绘带宽的增加对本文所提算法的成像质量影响不大。评价SAS成像算法优劣的指标通常包含两方面:3 dB脉冲响应宽度(impulse response width，IRW)和峰值旁瓣比(peak sidelobe ratio，PSLR)。表3对3种成像算法在方位向的脉压效果进行了对比，从结果可以看出本文算法在处理宽带宽测绘带数据时具有一定的优越性。

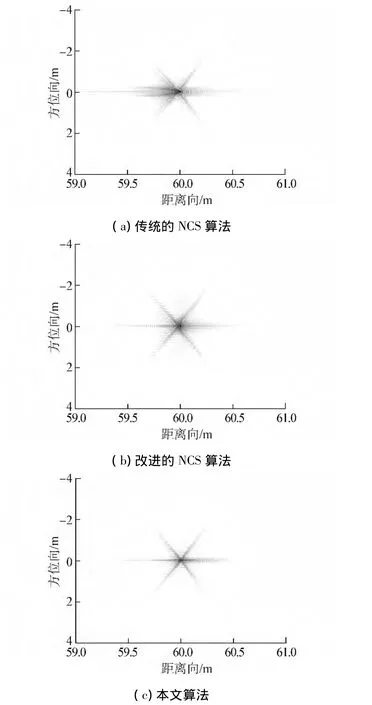
图5 边缘点(60 m，0 m)处点目标成像结果Fig.5 Imaging result of the edge point target located at(60 m，0 m)

表3 3种算法方位向脉压效果对比Table 3 Comparison of the azimuth compression effect processed by three different algorithms

5 结束语

针对宽带宽测绘带SAS成像的需求，本文继续改进NCS算法，通过保留距离向频率的四阶项，使得改进算法满足宽带需求，通过充分考虑等效调频斜率的一阶线性及二次非线性变化特性使得改进算法满足宽测绘带需求。由于本文在推导由三次和四次相位滤波及NCS操作引入的相关参量时，充分考虑了等效调频斜率随时延差量的二阶非线性变化，不仅有效提高了成像质量，而且大大提高了宽带条件下SAS成像的宽测绘带需求。遗憾的是，由于收发合置SAS系统的实测数据并不多见，因此本文没能进行实测数据成像试验。

由于水下声速较低，传统的收发合置SAS不能同时兼顾高的方位向分辨率和高的测绘速率，多子阵技术的提出有效的解决了这一问题。如何将本文所提算法应用于宽带宽测绘带多子阵SAS成像是下一步研究的主要内容。

［1］DOUGLAS B L，LEE H.Synthetic aperture active sonar imaging［C］//IEEE International Conference on Acoustics，Speech，and Signal Processing.San Francisco，USA，1992:37-40.

［2］SILKAITIS J M，DOUGLAS B L，LEE H.Synthetic-aperture sonar imaging:system analysis，image formation，and motion compensation［C］//Conference Record of the Twenty-Ninth Asilomar Conference on Signals，Systems and Computers.Pacific Grove，USA，1995:423-427.

［3］LI Y L，YAN S S，ZHU G F，et al.Ultra wide band synthetic aperture radar real time processing with a subaperture nonlinear chirp scaling algorithm［C］//International Asia-Pacific Conference on Synthetic Aperture Radar.Seoul，Korea，2011:1-4.

［4］HAYES M P，GOUGH P T.Broad-band synthetic aperture sonar［J］.IEEE Journal of Oceanic Engineering，1992，17(1):80-94.

［5］杨海亮，张森，唐劲松.宽测绘带多阵合成孔径声纳成像的仿真研究［J］.系统仿真学报，2011，23(7):1424-1428.YANG Hailiang，ZHANG Sen，TANG Jinsong.Study on Simulation of multiple-receiver synthetic aperture sonar imagery based on wide swath［J］.Journal of System Simulation，2011，23(7):1424-1428.

［6］RANEY R K，RUNGE H，BAMLER R，et al.Precision SAR processing using chirp scaling［J］.IEEE Transactions on Geoscience and Remote Sensing，1994，32(4):786-799.

［7］CHANG C Y，JIN M，CURLANDER J C.Squint mode SAR processing algorithms［C］//Geoscience and Remote Sensing Symposium，12th Canadian Symposium on Remote Sensing.Vancouver，Canada，1989:1702-1706.

［8］DAVIDSON G W，CUMMING I G，ITO M R.A chirp scaling approach for processing squint mode SAR data［J］.IEEE Transactions on Aerospace and Electronic Systems，1996，32(1):121-133.

［9］WANG K Z，LIU X Z.Improvement of non-linear chirp scaling algorithm［C］//International Conference on Computational Electromagnetics and its Applications.Beijing，China，2004:391-394.

［10］AN D X，HUANG X T，JIN T，et al.Extended nonlinear chirp scaling algorithm for high-resolution highly squint SAR data focusing［J］.IEEE Transactions on Geoscience and Remote Sensing，2012，50(9):3595-3609.

［11］SUN G C，XING M D，LIU Y，et al.Extended NCS based on method of series reversion for imaging of highly squinted SAR［J］.IEEE Geoscience and Remote Sensing Letters，2011，8(3):446-450.

［12］SUN G C，JIANG X W，XING M D，et al.Focus improvement of highly squinted data based on azimuth nonlinear scaling［J］.IEEE Transactions on Geoscience and Remote Sensing，2011，49(6):2308-2321.

［13］NIEVES E G，LOPEZ J M，VILLALOBOS C P.Extension of the chirp scaling algorithm to 3-D near-field wideband radar imaging［J］.IEEE Proceedings Radar，Sonar and Navigation，2003，50(3):152-157.

［14］POTSIS A，REIGBER A，MITTERMAYER J，et al.Improving the focusing properties of SAR processors for wideband and wide-beam low frequency imaging［C］//IEEE International Geoscience and Remote Sensing Symposium.Sydney，Australia，2001:3047-3049.

［15］刘光平.超宽带合成孔径雷达高效成像算法［D］.长沙:国防科技大学，2003:47-57.LIU Guangping.Efficient imaging generation for ultra-wide band synthetic aperture radar［D］.Changsha:National U-niversity of Defense Technology，2003:47-57.

［16］杨海亮.多接收阵合成孔径声纳成像算法研究［D］.武汉:海军工程大学，2009:106-118.YANG Hailiang.Studies on imaging algorithm of multiplereceiver synthetic aperture sonar［D］.Wuhan:Naval University of Engineering，2009:106-118.