边坡稳定分析的颗粒流方法研究

张小雪，王滨生，迟玉鹏，吕志强

(1.哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001;2.黑龙江省六建建筑工程有限责任公司，黑龙江哈尔滨150076)

滑坡是一种较频发的自然灾害，滑坡运动问题属于动力学问题，目前，研究人员对滑坡进行稳定性分析时大多采用极限平衡法［1］，这种方法没有考虑土体中颗粒之间的相对运动及变形，只考虑静力平衡条件和土的摩尔－库仑准则，从而可知，这种方法不能很准确地表述滑坡运动的特点［2］。数值分析方法考虑了土体的应力－应变关系，其中有限单元法基于连续性假设，是数值模拟在边坡稳定分析中应用最早的，但有限元法不能求解滑坡的大变形和大位移。离散元法其突出功能是在反应土颗粒之间接触面的滑移、分离及侧翻等大位移的同时，又能计算土颗粒内部的变形与应力分布。颗粒流(particle flow code，PFC)方法是离散元法中一种特殊的方法，在颗粒流中，把单元都看作是刚性的圆形或球形的颗粒，这种单元构成较符合散体介质的特性，所以对散体介质用颗粒流方法分析较为准确［3-4］。进行颗粒流分析时，在土样应力－应变关系曲线已知的情况下，一个关键的问题是如何获取能反映材料宏观特性的细观参数，目前应用最多的是通过双轴压缩试验不断调整细观参数与宏观特性，最终匹配得到合理的细观参数［5］。近年来，徐小敏等［6-8］对粘性材料的抗剪强度参数与颗粒流细观参数联系起来，真实反映粘性材料剪切特性，为正确有效地选取颗粒细观参数提供了依据。

1 接触本构关系

在PFC2D(particle flow code in 2 dimensions)中，材料的本构特性是通过接触本构模型来模拟的。接触模型有3种，即接触－刚度模型、滑动和分离模型和粘结模型。其中接触－刚度模型有线性模型和Hertz-Mindlin模型2种。线性接触模型通过法向和切向刚度定义，用假定接触实体的接触刚度是串联的方法来计算联合刚度。Hertz-Mindlin模型是非线性刚度模型，适用于模拟无粘结、应变小的情况。滑动和分离模型是2个接触实体的内在特性，采用限制剪切力的方式，无法向抗拉强度，并允许滑动。粘结模型有2种，即接触粘结模型和平行粘结模型。接触粘结是球与球之间通过一点发生接触，对于两个相互接触的颗粒，无法控制其相对转动。所以，接触粘结只可以传递力;平行粘结模拟颗粒接触后还有其他粘结作用的情况，该作用粘结的有效刚度与颗粒接触点刚度采用并联连接，平行粘结可以传递力和力矩来阻止颗粒转动［9-10］。接触粘结和平行粘结可以同时设置，这样可以使颗粒间有最小的相对运动。

2 数值试样试验

一般工程计算中，材料的特性是通过宏观参数来描述的，这些宏观参数往往是由实验得到，或由实验参数派生的，而对离散元理论，需要输入的是土体的细观参数，由细观参数来反映宏观参数，为能正确反映宏观参数，首先必须建立正确的宏－细观参数的关系。采用PFC2D程序进行双轴试验的颗粒流模拟，构造四周边界约束的长方形试样，顶部和底部约束模拟加载，左右两边的约束模拟试样边界施加的限制。试验中，颗粒流程序自动记录墙体和颗粒的运动过程和位置及颗粒之间的相互作用情况，得到颗粒和墙体运动的宏观数据［11］。

2.1 试样颗粒生成

先创建几何尺寸为h×b=70 mm×35 mm的矩形试样，该试样由4道没有摩擦的墙围成(见图1)，在PFC模型中，主要的控制参数见表1。

图1 球面冲击波作用于刚性平板示意图Fig.1 The spherical shock wave acting on a rigid plate

为了使PFC模型更好的模拟土试样的不均匀特性，颗粒单元半径R采用从最小值Rmin到最大值Rmax的正态分布，取Rmin=0.25 mm，Rmax=0.5 mm。模型生成后，利用两侧向、顶部、底部墙体的运动，对试样施加等向固结围压σ0，即σx=σy=σ0。σx和σy按下式计算:

式中:fx为左/右侧墙体与颗粒单元在X方向接触力;fy为顶/底部墙体与颗粒单元在Y方向接触力;r为所有颗粒单元的平均半径:

用下列关系计算X、Y方向上的应变［15］:

表1 粘性土PFC模型的输入参数Table 1 PFC model input parameters of clay

2.2 土体宏、细观力学参数关系分析

图2为在围压σ3=100 kPa下，颗粒摩擦系数μ分别取0.5、0.9时，不同颗粒接触强度C的土样的应力－应变曲线。

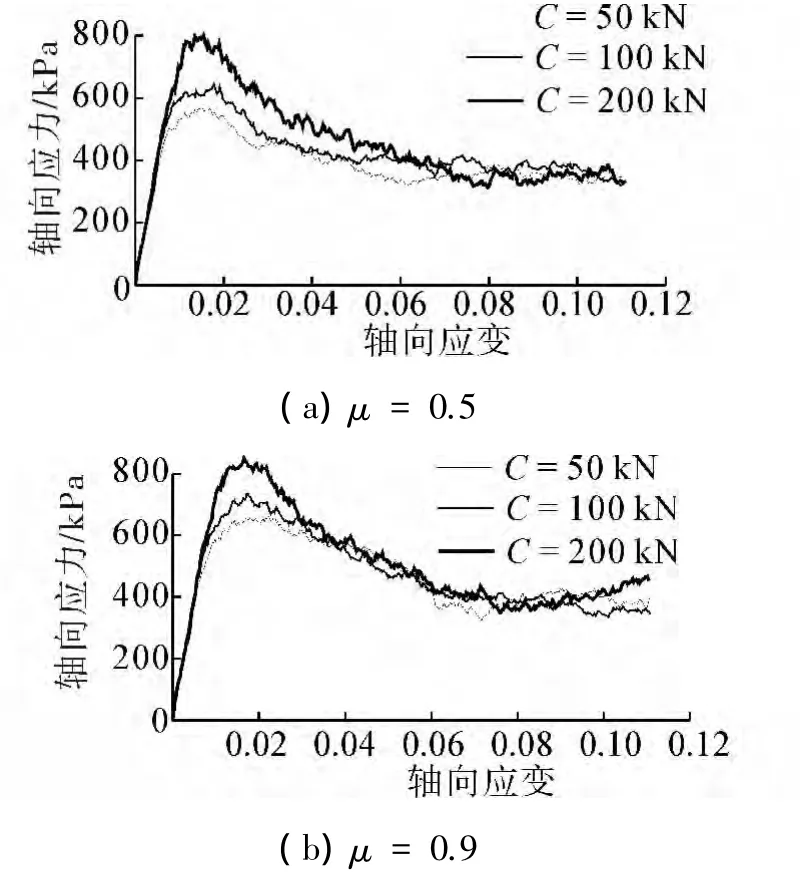
图2 围压100 kPa下的应力－应变曲线Fig.2 Stress-strain curves with 100 kPa confining

从图2(a)可以看出在施加相同围压的情况下，具有相同摩擦系数，不同颗粒接触强度的试样，其峰值强度随接触强度的增大而增大，可见接触粘结强度对峰值强度有较大的影响，说明粘结强度是影响粘土的主要因素之一，同时，随着粘结强度的增大，曲线表现出较大的软化特性。比较图2(a)和(b)可以看出:具有相同颗粒接触强度的试样，随着摩擦系数的增大峰值强度增大，可见摩擦系数主要影响土试样的峰值强度。

图3 试样双轴压缩力学响应的应力－应变曲线Fig.3 Stress-strain behavior of biaxial testing

图 3 为具有相同摩擦系数 μ=0.5、0.9，接触强度C分别为50、100、200 kN，在不同的围压下得到的土试样的应力－应变曲线。

图4 摩尔－库仑破坏包络线Fig.4 Failure envelopes of Mohr-Coulomb

比较图3中在不同摩擦系数下，其他参数相同的应力－应变曲线，可以明显的看到，各条试验曲线的切线弹性模量是一样的，在该区域内，粘土的强度是由接触粘结决定的，不论摩擦系数多少，都不会对粘土强度有影响，当接触粘结破坏后，峰值强度随着摩擦系数的增大而增大。

根据图3的加载结果，得到了峰值强度，以此作为绘制摩尔应力圆的基本参数。图4为颗粒摩擦系数相同，接触强度不同的两组摩尔－库仑包络线，从图可以看出，每组图的包络线接近平衡，也就是说，试样的摩擦角不变，这说明颗粒摩擦系数是影响试样摩擦角的唯一因素;在对比两组图来看，试样的粘聚力与颗粒摩擦系数和接触强度有关。在摩擦系数相同的条件下，粘聚力随接触强度的增大而增大，而在接触强度相同的条件下，粘聚力随摩擦系数的增大而减小。

由此可见，在进行模拟分析时，可以根据得到的材料细观参数与宏观特性的关系调整细观参数的数值，使用PFC方法模拟得到的应力－应变曲线与室内实验得到的应力－应变曲线相符。

3 边坡稳定颗粒流模拟

3.1 模型的建立

根据土体宏、细观力学参数关系，按表2的参数取值，对粘性土坡进行数值模拟分析。

表2 边坡的细观参数Table 2 Micro-parameter of slope

建立模型时先构建四面墙体，然后用扩大粒径的方式生成颗粒，达到室内试验所用式样的孔隙率后，让生成的颗粒在自重下运动，最终达到平衡，平衡后根据所模拟的边坡形状，将多余的颗粒删除，最后形成符合宏观参数的边坡模型。为便于观察滑裂面的发生发展及滑坡破坏的全过程，用不同的颜色标记颗粒［12］。此外，因为删除多余的颗粒，使模型底部失去约束，应力释放，故需要在进行一次迭代计算，达到平衡。在迭代计算过程中，体系的最大不平衡接触力随迭代次数的增加逐渐收敛于0，即体系达到了力学平衡状态，运算结束［13］。

3.2 模拟结果及分析

采用PFC2D程序对滑坡的发生、发展的全过程进行仿真模拟。选择时间为30 000步、70 000步、100 000步、140 000步的4张图片作为典型图片来分析，见图5，从t=30 000步的图可见，滑坡发生时先从坡顶出现微小的开裂，随着微裂缝的发生，坡面上裂缝自上向下扩大，坡脚在上部块体的重压下滑动加剧，裂缝加大，直至出现剪切破坏，这时，边坡顶部块体开始向下快速滑落，边坡底部土体因受重压而变形，剪切带自上而下贯通，最终形成圆弧形滑裂面。

图5 粘性土坡破坏图Fig.5 Destruction of cohesive soil slope

图6是粘性土坡颗粒的位移矢量图，从颗粒位移的变化及滑裂面形成的位置来看，用PFC2D程序对滑坡进行模拟符合滑坡演化规律，且与室内试验的模拟结果吻合度较好。

图6 粘性土坡颗粒位移矢量图Fig.6 Displacement vectograph of cohesive soil slop

4 结论

1)利用PFC颗粒流软件模拟双轴试验，以此绘制摩尔应力圆，对土试样的宏观强度指标与其对应的细观参数之间的关系进行分析，结果表明，模型中各颗粒之间的摩擦系数，对试样的摩擦角和试样的粘聚力都有影响，而颗粒间的接触强度只影响试样的粘聚力，对试样的摩擦角没有影响。在摩擦系数相同的条件下，粘聚力随接触强度的增大而增大，而在接触强度相同的条件下，粘聚力随摩擦系数的增大而减小。

2)利用本文所得到的宏－细观参数之间的关系，用PFC2D程序对宏观参数已知的土试样进行模拟，通过与土试样的室内实验结果比较，可以得出，用PFC2D程序进行双轴试验模拟，所建立的土试样宏－细观参数之间的关系是可行的。

3)采用PFC2D程序模拟滑坡变形破坏时，可以不需要先假设滑裂面的位置，而是颗粒根据受到的接触力自行运动，在抗剪强度最弱的地方，颗粒分开，形成滑裂面。土颗粒在自重下形成滑坡，是土坡因为自身强度过小而形成的，首先在坡顶处形成小的开裂面，随着时间的变化，开裂面逐渐扩大，最终形成贯穿上下的滑裂面，其受力特点是:滑坡上部受拉，中部受剪，下部受压，与边坡的实际受力情况相吻合，充分体现了采用离散元法进行边坡稳定性分析的优越性。

［1］贾东远，阴可，李艳华.岩石边坡稳定性分析方法［J］.地下空间，2004，24(2):250-255.JIA Dongyuan，YIN Ke，LI Yanhua.Rock slope stability analysis method［J］.Underground Space，2004，24(2):250-255.

［2］杜永彬.太大公路徐家寨滑坡运动的数值模拟［J］.重庆交通大学学报，2008，27(6):1099-1102.DU Yongbin.Numerical simulation of the land slide movement in Xujiazhai in the high way from Taiyuan to Dalian［J］.Journal of Chongqing Jiaotong University，2008，27(6):1099-1102.

［3］廖雄华，周健，吴世明，等.粘性土平面应变试验颗粒流模拟可行性研究［J］.佛山科学技术学院学报，2002，20(2):33-38.LIAO Xionghua，ZHOU Jian，WU Shiming，et al.Feasibility study of the simulation of plane strain test by particle flow code on clay［J］.Journal of Foshan University，2002，20(2):33-38.

［4］刘洋，吴顺川，周健.单调荷载下砂土变形过程数值模拟及细观机制研究［J］.岩土力学，2008，29(12):3199-3216.LIU Yang，WU Shunchuan，ZHOU Jian.Numerical simulation of sand deformation under monotonic loading and mesoscopic mechanism analysis［J］.Rock and Soil Mechanics，2008，29(12):3199-3216.

［5］王培涛，杨天鸿，于庆磊，等.节理边坡岩体参数获取与PFC2D应用研究［J］.采矿与安全工程学报，2013，30(4):560-565.WANG Peitao，YANG Tianhong，YU Qinglei，et al.On obtaining jointed rock slope geo-parameters and the application of PFC2D［J］.Journal of Mining and Safety Engineering，2013，30(4):560-565.

［6］徐小敏，凌道盛，陈云敏，等.基于线性接触模型的颗粒材料细-宏观弹性常数相关关系研究［J］.岩土工程学报，2010，32(7):991-999.XU Xiaomin，LING Daosheng，CHEN Yunmin，et al.Correlation of microscopic and macroscopic elastic constants of granular materials based on linear contact model［J］.Chinese Journal of Geotechnical Engineering，2010，32(7):991-999.

［7］周博，汪华斌，赵文峰，等.粘性材料细观与宏观力学参数相关性研究［J］.岩土力学，2012，33(10):3171-3178.ZHOU Bo，WANG Huabin，ZHAO Wenfeng，et al.Analysis of relationship between particle mesoscopic and macroscopic mechanical parameters of cohesive materials［J］.Rock and Soil Mechanics，2012，33(10):3171-3178.

［8］尹成薇，梁冰，姜利国.基于颗粒流方法的砂土宏-细观参数关系分析［J］.煤炭学报，2011，36(2):264-267.YIN Chengwei，LIANG Bing，JIANG Liguo.Analysis of relationship between macro-micro-parameter of sandy soil based on particle flow theory［J］.Journal of China Coal Society，2011，36(2):264-267.

［9］张晓平，吴顺川，张志增，等.含软弱夹层土样变形破坏过程的细观数值模拟分析［J］.岩土力学，2008，29(5):1200-1204.ZHANG Xiaoping，WU Shunchuan，ZHANG Zhizeng，et al.Numerical simulation and anaiysis of failure process of soil with weak intercalated layer［J］.Rock and Soil Mechanics，2008，29(5):1200-1204.

［10］王宇，李晓，王声星，等.滑坡渐进破坏运动过程的颗粒流仿真模拟［J］.长江科学院院报，2012，29(12):46-52.WANG Yu，LI Xiao，WANG Shengxing，et al.The particle flow simulation of dynamic process of landslide failure［J］.Journal of Yangtze River Scientific Research Institute，2012，29(12):46-52.

［11］周健，池毓蔚，池永，等.砂土双轴试验的颗粒流模拟［J］.岩土工程学报，2000，22(6):701-704.ZHOU Jian，CHI Yuwei，CHI Yong，et al.Simulation of biaxial test on sand by particle flow code［J］.Chinese Journal of Geotechnical Engineering，2000，22(6):701-704.

［12］周健，廖雄华，池永，等.土的室内平面应变试验的颗粒流模拟［J］.同济大学学报，2002，30(9):1044-1050.ZHOU Jian，LIAO Xionghua，CHI Yong，et al.Simulating plane strain test of soils by particle flow code［J］.Journal of Tongji University，2002，30(9):1044-1050.

［13］周健，王家全，曾远，等.土坡稳定分析的颗粒流模拟［J］.岩土力学，2009，30(1):86-90.＇ZHOU Jian，WANG Jiaquan，ZENG Yuan，et al.Simulation of slope stability analysis by particle flow code［J］.Rock and Soil Mechanics，2009，30(1):86-90.