基于Moors谱峭度图的高速列车轴承故障诊断方法

彭 畅，王 旭，张志波，薛 源

PENG Chang, WANG Xu, ZHANG Zhi-bo, XUE Yuan

（南车青岛四方机车车辆股份有限公司 技术中心，青岛 266111）

0 引言

近年来高铁推动了我国铁路沿线区域经济及文化的发展，而如何确保高速列车在高速状态下的安全、可靠运行具有至关重要的意义。轴承作为列车转向架系统的关键零部件之一，针对其早期故障监测与诊断的研究对于及时进行故障报警并避免重大安全事故发生十分必要[1]。

然而，由于高速列车运行环境复杂多变，轴承信号易受背景噪声及其他零部件的干扰，传统频谱分析方法不能有效地提取轴承故障特征。尚万峰等[2]提出了基于三阶累积量最小二乘及最小均方误差自适应算法的列车轴承故障诊断方法，有效地降低了强背景噪声干扰并提高了故障特征信号分离准确率。刘方等[3]研究了基于时域多普勒较正和EEMD的列车轴承声信号故障诊断，有效地提取了轴承内外圈局部故障特征。王靖等[4]研究了基于数据插值重采样技术的诊断方法，利用整周期采样技术、等角度重采样技术以及特征谱提取技术等联合分析方法准确识别了列车轴承频带变化类非线性故障振动信号。

谱峭度图算法由于能够衡量轴承振动信号中的瞬态冲击程度，从而识别故障特征最为明显的成份所在的频带并为后续解调分析提供依据，得到了广泛关注与迅速发展。Antoni和Randall[5]提出了基于短时傅里叶变换的谱峭度图及其快速算法，成功过滤出故障瞬态信号成分。Lei等[6]提出了改进的基于小波包变换的谱峭度算法，从而提高了轴承微弱故障特征提取的准确性。在以上分析的基础上，本文针对列车轴承故障诊断中的强噪声干扰问题，提出了一种基于Moors谱峭度图算法的诊断方法，不仅消除了背景噪声对轴承故障信号的影响而且改善了四阶矩谱峭度图算法中存在的不稳定性问题，从而有效并准确地提取出了列车轴承故障特征。

1 谱峭度

当列车轴箱轴承内部出现局部故障时，其振动信号往往呈现周期性的瞬态冲击特性，而峭度作为一个无量纲统计量则能够衡量振动信号的冲击程度。离散型时域信号s(n)的峭度值可以计算为：

其中µ和σ分别为信号s(n)的均值及方差，K值越大则表示信号冲击特性越明显。

为了在频域内识别信号s(n)中瞬态冲击较明显的成份所处的频带位置，Antoni和Randall[5]定义了谱峭度的概念。离散型非平稳信号s(n)的Wold-Cramér分解式为：

其中S(n,f)是s(n)在频率f处的复包络谱值。则基于四阶矩累积量的谱峭度为：

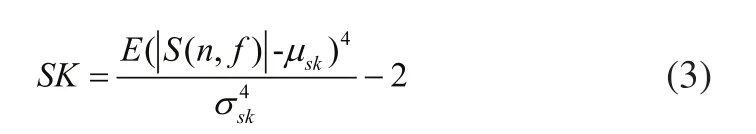
其中µsk和σsk分别为信号的均值及方差，由于包络信号是复值，修正常数设定为-2。

2 Moors谱峭度图

然而式(1)所示的四阶矩峭度系数及式(3)所示的四阶矩谱峭度系数容易受到信号中奇异值的影响而导致其反映的信号瞬态冲击程度产生偏差。为了克服传统谱峭度系数所存在的非鲁棒性问题，本文定义了能够完全消除奇异值影响的Moors谱峭度系数：

其中Ei表示累积分布函数F的第i八分位数：

为了确定信号s(n)在 平面内的谱峭度值分布规律，将原始信号进行短时傅里叶变换，然后计算在短时傅里叶变换滤波器组滤波后子信号的Moors谱峭度值分布。在 平面内的Moors谱峭度图上最大谱峭值对应的中心频率fc及及带宽Δfc即为后续包络解调分析所需要的解调频带信息。

在上述理论分析的基础上，针对高速列车轴承振动信号易受复杂工况下背景噪声及其他部件振源的影响导致传统频谱分析方法失效的问题，提出了基于Moors谱峭度图的高速列车轴承故障诊断方法，其具体流程如图1所示。

1）计算原始信号s(n)的短时傅里叶变换；

2）计算短时傅里叶变换后各子信号的Moors谱峭度值；

3）在 平面内铺砌信号s(n)的Moors谱峭度图，确定最大谱峭度值分量所在的中心频率及带宽；

4）以步骤3）中所确定的频带信息为依据，对信号进行包络解调分析；

5）对比列车轴承故障计算特征频率，诊断该轴承信号中是否存在故障特征频率信息。

图1 基于Moors谱峭度图的高速列车轴承故障诊断方法

3 高速列车轴承试验平台

如图2所示为本文所采用的高速列车轴承试验平台，其中轮对一侧安装故障轴承，另外一侧安装正常轴承，型号为SNy563的压电式加速度传感器安装在轮对轴箱外侧。该试验平台能够根据不同的轴承故障及工况设定从30km/h～200km/h之间的5个不同速度等级，如表1所示。此外根据轴承具体参数所计算的故障特征频率系数如表2所示。

图2 高速列车轴承试验平台

表1 高速列车轴承试验平台速度等级

表2 高速列车轴承故障计算特征频率

4 高速列车轴承振动信号分析

为了验证本文所提出的基于Moors谱峭度图的高速列车轴承故障诊断方法的有效性及优越性，对在上一节介绍的轮对轴承试验平台上采集的轴承振动信号进行分析。

当轮对转速为100km/h时，即对应的转频为fi=10.29Hz时，时间长度为10s的正常轴承时域振动信号及其频谱与包络谱如图3所示。从传统频谱图中看不到任何有用信息，而传统的包络谱中则可以看到转频的倍频成份，说明该轴承属于正常状态。对原始信号s(n)进行短时傅里叶变换，并分析其四阶矩谱峭度图，如图4所示。谱峭度值最大（黑色虚线框所示）的子信号对应中心频带为625Hz，分解层数为5.5。以该参数为包络解调依据，经带通滤波后的信号及包络谱如图5所示。对比原始信号与滤波后信号的时域特征，由于轴承属于正常状态，因此不存在瞬态冲击特征，此外滤波后信号的包络解调谱中只有转频及其倍频成份。

图3 正常轴承原始信号及频谱

图4 正常轴承原始信号基于短时傅里叶变换的四阶矩谱峭度图

图5 传统谱峭度图滤波后信号及其包络谱

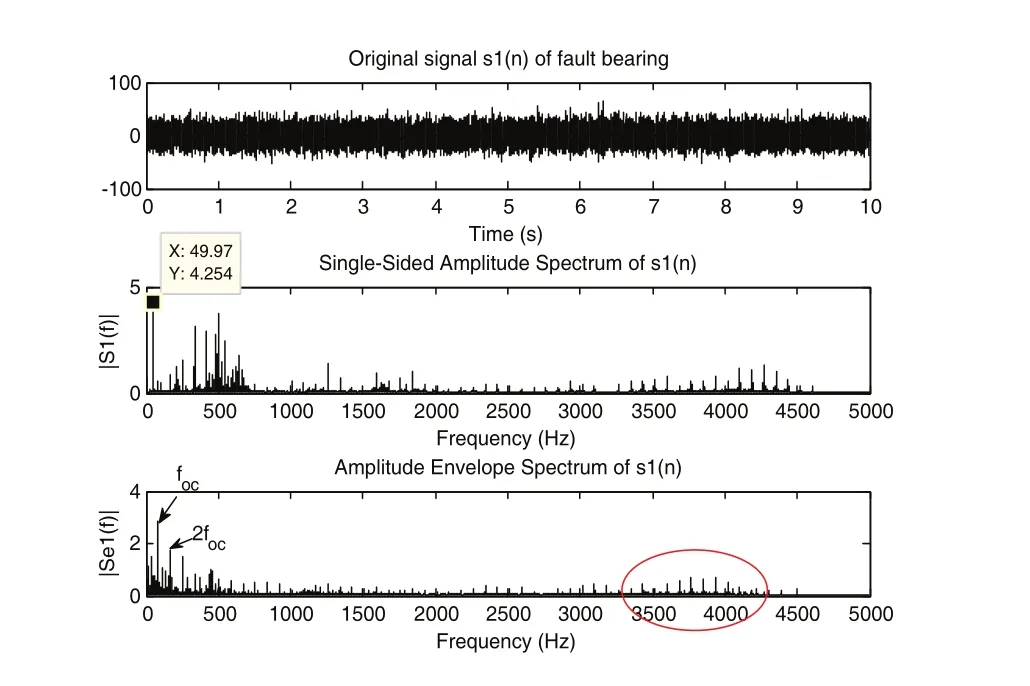
图6 外圈故障轴承时域信号及频谱

同样当轮对转速为100km/h时，时间长度为10s的外圈故障轴承（根据表2计算的轴承外圈故障特征频率foc=83.35Hz）时域振动信号s1(n)及其频谱如图6所示，由于受强背景噪声及高频调制现象的影响，故障信号的频谱不能识别任何故障特征信息，而故障信号的包络谱中虽然可以看到外圈故障特征频率成份及其倍频，但受到其他频率成份干扰，此外高频带上存在冲击特征，需要进一步调整解调频带参数，增加了诊断难度。对信号s1(n)进行短时傅里叶变换，并分析其四阶矩谱峭度图，如图7所示。谱峭度值最大（黑色虚线框所示）的子信号对应中心频带为2187.5Hz，分解层数为5，随后进行包络解调分析，结果如图8所示。从图8中可以看到滤波后的信号中瞬态冲击成份得到明显增强，且在其包络谱中发现外圈故障频率foc及其倍频，但是受到其他频率成份干扰，不利于诊断。

图7 外圈故障轴承信号基于短时傅里叶变换的四阶矩谱峭度图

图8 传统谱峭度图滤波后故障信号及其包络谱

计算信号s1(n)经短时傅里叶变换后的Moors谱峭度图，如图9所示。相对于图7所示的传统四阶矩谱峭度图，图中显示的同样第5分解层上的最大谱峭度值对应解调频带中心处在高频带上（4375Hz），与轴承故障存在的高频调制现象一致。图10为滤波后信号及其包络谱，可以清楚发现滤波后信号中的故障瞬态冲击特征相对于原始信号同样得到显著增强，此外滤波信号包络谱中存在明显外圈故障特征频率及其倍频成份，而且不存在其他干扰频率影响，可以明确诊断出该轴承存在外圈故障。

图9 外圈故障轴承信号基于短时傅里叶变换的Moors谱峭度图

图10 Moors谱峭度图滤波后故障信号及其包络谱

5 结论

由于高速列车轴承振动信号中存在强噪声干扰问题及调制现象，传统的频谱分析无法有效识别故障特征频率，而传统的包络解调谱中虽然能够识别故障特征频率，但是仍然受其他频率信息干扰，此外解调频带参数需要人为选择，不具有自适应特性，影响诊断效果。而基于四阶矩谱峭度图算法的故障诊断方法虽然能一定程度上识别故障频率，但结果不具有鲁棒性。本文提出了一种基于Moors谱峭度图的高速列车轴承故障诊断方法，不仅消除了背景噪声对轴承故障信号的影响而且改善了传统谱峭度图算法中存在的不稳定性问题，试验结果分析很好地验证了该方法的有效性及优越性，说明其具有良好的工程应用价值。

[1]张翱.列车轴承故障道旁声学诊断关键技术研究[D].中国科学技术大学,2014.

[2]尚万峰,赵升吨,韩捷.基于高阶累积量自适应算法的列车轴承的故障诊断[J].振动工程学报,2006,19(2)：234-237.

[3]刘方,沈长青,何清波,胡飞,张翱,孔凡让.基于时域多普勒校正和EEMD的列车轴承道旁声音监测故障诊断方法研究[J].振动与冲击,2013,32(24)：104-109.

[4]王靖,陈特放,黄采伦,周华.列车轴承频带变化类故障的诊断方法[J].北京工业大学学报.2012,38(5)：678-682.

[5]J.Antoni and R.B.Randall, The spectral kurtosis：application to vibratory surveillance and diagnostics of rotating machines[J].Mechanical system and signal processing,20(2006)308-331.

[5]Y.G.Lei, J.Lin, Z.J.He, et al., Application of an improved kurtogram method for fault diagnosis of rolling element bearings[J].Mechanical system and signal processing,25 (2011)1738-1749.