Chung型对数律精确渐近性的一个注记
邹广玉
(长春工程学院 理学院,吉林 长春 130012)
Chung型对数律精确渐近性的一个注记
邹广玉
(长春工程学院 理学院,吉林 长春 130012)
利用独立同分布序列生成线性过程部分和的Berry-Esseen不等式,将独立同分布序列Chung型对数律精确渐近性的结果推广到线性过程,丰富了线性过程精确收敛速度的结果.
Berry-Esseen不等式;对数律;精确渐近性
1 引言及主要结论

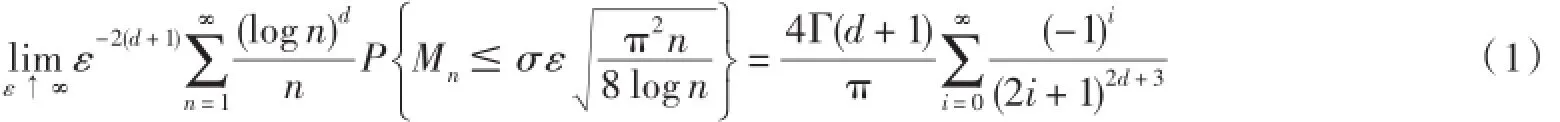
i
本文的目的是针对独立同分布序列生成的线性过程 ,建立如式(1)的结果.先给出线性过程的定义.
设{εi,-∞<i<∞}为同分布随机变量列,均值为0,方差有限,{ai,-∞<i<∞}为一绝对可和的数列,定义线性过程为关于线性过程的Chung型对数律的精确渐近性结果已有一些,如文献[4-5],但其结论多为如下形式:其中N表示标准正态随机变量,下同.


本文给出类似式(1)的结果.



2 若干引理
在本文中,记{W(t),t≥0}为标准Wiener过程,C表示正常数,在不同的位置表示不同的值.
引理1对任意的x>0,有
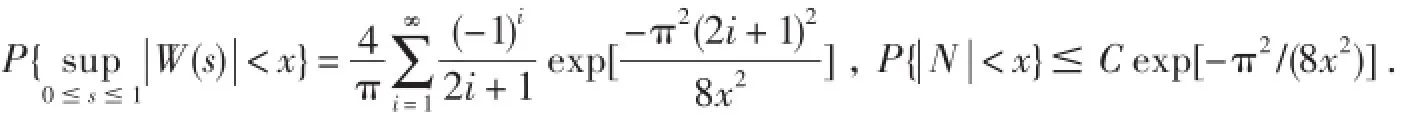
证明见文献[3]引理1.
引理2在定理1的条件下,有
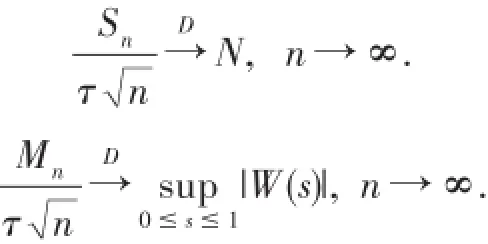
证明定理1的条件显然满足文献[4]中引理2.1的条件,由此可得本引理结论.
引理3在定理1的条件下,有

证明由文献[6]式(2.2)可得.
3 定理1的证明
不失一般性,不妨设τ=1.令a(ε)=[eMε2],M>4.定理1可由以下几个命题推得.
命题1对任意的d>-1,有

证明见文献[3]命题1.
命题2对任意的M>4,有


证明由引理2可知,由Toeplitz引理[7],易得

进而

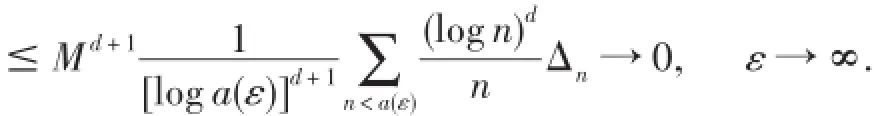
命题3对任意的d>-1,有

证明见文献[3]引理5.
命题4对任意的d>-1,有

证明由引理1和引理3,有

故有

先令ε→∞,再令M→∞,即得命题结论.
由命题1-4及三角不等式可得(2)式,从而定理1得证.
[1]Pang Tian-xiao,Lin Zheng-yan.Precise rates in the law of logarithm for i.i.d.random variables[J].Comput Math Appl,2005,49: 997-1010.
[2]Fu Ke-ang,Zhang Li-xin.Precise rates in the law of logarithm for negative associated random variables[J].Comput Math Appl, 2007,54:687-698.
[3]傅可昂.PA序列Chung型对数律的极限定理[J].浙江大学学报:理学版,2010,37(6):625-628.
[4]刘君,董志山,张勇.由强混合序列生成线性过程精确渐近性的一般形式[J].吉林大学学报:理学版,2008,46(4):595-600.
[5]Zhang Yong,Zhao Shi-Shun,Dong Zhi-shan.Precise asymptotics in the law of large numbers and the law of the iterated logarithm of moving-average process generated by ALNQD sequences[J].Northeast Math J,2007,23(6):549-562.
[6]李云霞.线性过程关于矩的重对数律[J].应用数学,2011,24(3):554-561.
[7]Stout W F.Almost sure convergence[M].New York:Academic Press,1995:120.
A Note on Precise Asymptotics in the Chung-type Law of Logarithm
ZOU Guang-yu
(School of Science,Changchun Institute of Technology,Changchun 130012,China)
Applying the Berry-Esseen inequality of linear process generated by the independent and identically distributed random variables,the author of this paper extended the precise asymptotic results of Chung's loga⁃rithm law from the independent and identically distributed sequences to linear process,which enriched the re⁃sult of the convergence rates of the linear process.
Berry-Esseen inequality;law of the logarithm;precise asymptotics
O211.4
A
1008-2794(2015)02-0103-03
2014-04-14
国家自然科学基金项目“随机传染病模型的渐近性质的研究与预测”(11401090);长春工程学院青年基金项目“概率极限理论在破产理论中的应用”(320130019)
通讯联系人:邹广玉,讲师,博士,研究方向:概率极限理论,E-mail:jingyang999@126.com.

