基于㶲损失分析的反应精馏塔板上反应体积的优化设计

林子昕，安维中，袁琳皓，蔡浩，朱建民

（1 中国海洋大学化学化工学院，山东 青岛 266100；2 辽宁奥克化学集团，辽宁 辽阳 111003）

引 言

反应精馏（reactive distillation）是将反应与分离结合在一个操作单元中的典型的过程强化技术，迄今已成功用于150 多种化学品的工业化生产[1-3]。同时，反应精馏属于典型的能量密集型过程，如何实现能量的优化利用一直是人们关注的热点问题。近十几年来，研究者从不同层面探讨了反应精馏过程能量的集成优化问题[3]，提出了热泵反应精馏[4]、内部热集成反应精馏[5]、反应精馏隔壁塔[6]等节能流程。然而注意到，这些研究多从热力学第一定律角度考虑系统节能问题，且主要针对平衡（可逆）反应体系，鲜见有热力学第二定律方面的研究报道。Almeida-Rivera 等[7]从经济学、㶲损失等几方面考虑，提出了改善热力学效率的反应精馏塔设计方法，但注意到其方法有效性也是通过可逆反应体系（甲基叔丁基醚）进行验证。由此可见，将基于热力学第二定律的热力学分析法应用于以选择性为目标的反应精馏塔的设计是个值得研究的课题。

在反应精馏塔的设计中，反应段塔板上反应体积及其分配是重要的设计参数。对于非催化体系或均相催化体系，反应体积通常用液相持液量表示，对于非均相催化体系，通常用催化剂质量或体积表示。为方便表述，本文统一使用反应体积。反应精馏塔中反应体积的设计涉及两个层次的问题：一是确定总反应体积，二是确定反应段每块塔板上的反应体积，即反应体积的分配。对于总反应体积的确定，目前主要采用两种方法：一是根据Damkohler数所表征的停留时间与反应时间之间的关系加以确定[8]，二是采用多个平推流反应器-分离器的串联模型对反应精馏塔进行简化设计[9]。对于反应体积如何在塔板上分配问题，目前文献多采用等反应体积的设计，即将确定的总反应体积平均分配至反应段的每一块塔板[9-10]。需要说明的是，平均分配的方法对于平衡反应体系并无明显的负面影响，这是因为设计者主要关注每块塔板是否有足够大的反应体积使化学反应达到平衡，而对其分布并无严格限制。然而，对于以选择性为目标的不可逆连串反应体系则全然不同。首先，从动力学角度分析，反应体积直接影响反应程度，如果所有塔板上采用等反应体积设计，则必然导致目标产物在某些塔板上的停留时间过长，这势必增加了副反应发生的机率。其次，等反应体积分配将导致一些塔板上组分的熵产生速率过大，导致过程不可逆性增大，这在热力学第二定律方面是极其不利的。Ciric 等[11]强调了反应精馏塔塔板上反应体积设计的重要性和困难性，认为对于不受化学平衡限制的反应体系，反应塔板上的反应体积难以通过经验的方法或关联式确定，因此需要有一个优化技术来实现其设计。基于此，提出了基于混合整数非线性规划（MINLP）的优化设计方法。但数学规划方法的缺点是显而易见的，一是建模和求解非常复杂，二是缺乏对过程能量损失更深度的认识和分析[12]。

基于热力学第二定律的㶲的概念由Rant[13]于1956年提出，目前已广泛应用于能量密集型化工过程的节能研究。通过对过程的㶲进行计算，可以揭示过程内部由于不可逆性引起的㶲损失的原因和数量，可为制定相应的节能措施提供依据。迄今，㶲分析法已成功应用于换热网络[14]、透热精馏[15]等多个领域中，但鲜见在反应精馏领域的应用。本文针对以选择性为主要目标的反应精馏塔的节能问题，提出一种基于㶲损失分析的设计及优化策略，用于反应段塔板上反应体积分配的优化设计。方法的有效性通过环氧乙烷水合制乙二醇反应精馏体系进行验证。

1 反应精馏塔板上㶲的计算方法

图1为反应精馏塔中反应段第j块塔板的物流和㶲流示意图。对于稳态物系，当动能、位能的变化忽略不计时，物流㶲的大小取决于系统状态和环境状态（基态）的差异。这种差异既由物理参数（温度、压力等）不同而引起，也由组成（物质的化学结构、浓度等）不同而引起。前一种㶲称为物理㶲，后一种称为化学㶲。物流的总㶲为物理㶲与化学㶲的加和[16]，即

图1 反应精馏塔第j 个塔板上流股信息示意图Fig.1 Stream information of the j th stage in RD column

1.1 物理㶲的计算

物理㶲即经可逆的物理过程使物系温度与压力达到与环境呈平衡时所提供的那部分最大有用功。当环境状态为T0和p0时，对稳流物系，1 mol物质在T和p时的物理㶲可表示为

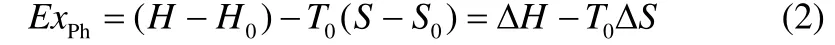
若物质在T0与T间的Ts发生相变，用γ表示相变焓，用β表示等压膨胀系数，则物理㶲可通过式(3)计算

1.2 化学㶲的计算

化学㶲即当物系经可逆扩散和化学反应过程达到与环境呈平衡时所提供的那部分最大有用功。由于涉及物质组成，在计算化学㶲时，除了要确定环境的温度和压力外，还需指定基准物和浓度。目前在基准物的选择上主要有Lother-Riekert 体系[17]，Szargut 体系[18]及龟山-吉田体系[19]。其中，龟山-吉田体系是目前被公认的较完善的㶲评价工具，本文采用该方法计算物流的化学㶲。

当选取298.15 K、101.325 kPa 作为环境的温度与压力时，纯物质的标准化学㶲可由式(4)进行计算

混合物的标准化学㶲可利用纯物质的标准化学㶲、混合物中各组分的摩尔分数xi及活度ai计算

如果系统为理想溶液或理想气体混合物，则式(5)可简化为

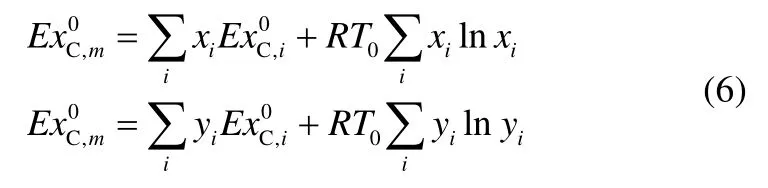
式(6)表明，混合物的标准化学㶲等于各纯组分所贡献的标准化学㶲以及在环境温度及压力下由于混合物组成与基准物组成不同而产生的扩散㶲之和[16]。

1.3 反应精馏塔板上㶲的计算

以图1所示的第j块反应精馏塔板为例，其输入㶲与输出㶲可分别写为式(7)与式(8)

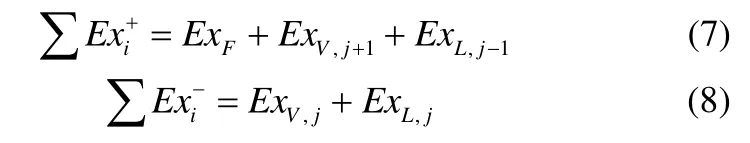
该塔板上的㶲损失即为

这里说明，以上㶲及㶲损失的计算公式均为通用方程，具体到特定的反应精馏体系，则需要一个计算ΔH、ΔS及活度a等参数的计算方法或模型。另外，考虑到非理想体系模型参数的计算的复杂性，本文将㶲计算和流程模拟技术相结合，以此保证计算的可靠性和准确性。

2 反应精馏塔板上反应体积设计与优化策略

2.1 问题描述

本文研究问题描述为：考虑一个以选择性为目标（主要针对不可逆、连串反应体系）的反应精馏塔，已知塔的操作参数（压力、原料进料配比）和设备参数（反应段和分离段的塔板数、原料进料位置），规定关键组分的转化率和目标产物的选择性，设计反应段各塔板上反应体积的分配，使系统的能耗达到最小（本文以再沸器负荷为评价标准）。

这里说明，反应精馏塔的优化还涉及操作压力、反应段和分离段的级数、进料位置等诸多参数，但由于这些参数的优化研究方法已比较充分（通常通过商业软件的灵敏度分析实现），所以本文研究仅考虑反应体积分配的优化设计问题。

2.2 方法策略及实施步骤

针对数学规划算法建模和求解的复杂性，本文提出一种基于过程模拟技术和㶲损失分析相结合的调优设计策略。这一方法的理论依据是：如果塔内反应塔板上的反应体积分配未优化，将导致某些塔板上㶲损失增大，这是导致系统能量利用不合理和热力学效率降低的重要因素[7]。基于此，本文建立一种简单的调优策略：将反应塔板上反应体积的分配和对应的㶲损失分布相关联，在总反应体积不变的条件下，如果某些塔板上㶲损失较大，则适当降低其反应体积，而对㶲损失较小的塔板，则适当 增加其反应体积，以此达到反应体积分配的优化 设计。

图2为本文方法的计算框图，采用再沸器负荷为塔的调节参数，而没有采用常用的回流比或再沸比，这是因为反应精馏塔的操作模式具有多样性，如有些塔采用塔顶物料全回流的操作模式[11],所以采用再沸器负荷来表示调节参数更具有普遍性。另外，图2除了对反应段塔板上反应体积（持液量）进行优化外，也对再沸器的负荷进行了优化（图2中的一个循环是调节再沸器负荷使目标产物选择性达到设定值，另一循环是使再沸器的负荷或系统 能耗达到最小）。本文方法的具体实施步骤描述 如下。

图2 反应精馏塔板上反应体积分配的优化设计框图Fig.2 Framework of design and optimization of reaction volume distribution in RD column

（2）将总的反应体积平均分配于反应段的各个塔板上，即取得反应体积分配的初值。在此条件下对塔进行模拟计算，并通过调节再沸器负荷使目标产物的选择性达到设计目标（目标产物选择性主要取决于再沸器负荷）。

（3）通过模拟计算取得反应段各塔板上的㶲损失分布，包括化学㶲及物理㶲损失，分析反应塔板上㶲损失分布的特征及其原因。

（4）将反应精馏塔板上的㶲损失分布和对应的反应体积分配关联起来，在总反应体积不变的条件下，通过制定的调优规则对塔板上的反应体积重新分配和逐步调优，直至再沸器负荷不再减小。

本文给出一种简单的调优策略：用Exloss,j表示反应段第j块塔板上的㶲损失，用量纲1 数fj表示第j块塔板上㶲损失的相对大小，即

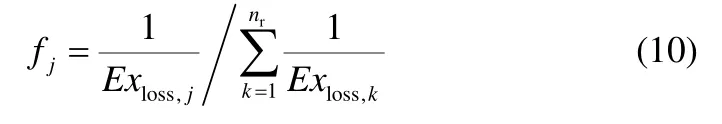
用Mj表示反应段第j块塔板上的反应体积，用nr表示反应段总塔板数，用α（0≤α≤1）表示调优系数，由式(11)计算新的反应体积分配

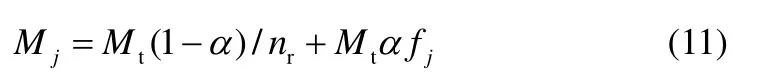
式(11)表明，Mj与其Exloss,j为反向关系，如果第j块塔板上Exloss,j较大（即fj较小），则降低Mj，反之增大Mj，且增减的数值与设定的α有关。当α为0 时，总反应体积在各板上平均分配；α数值越大，说明Mj的调整程度越大，当α为1 时，Mj与Exloss,j为反比关系。依此，以再沸器的负荷最小为目标，通过设定不同的α值进行调优，可以确定优化的Mj。

3 实例研究

3.1 过程特征及模拟计算方法

本文以广泛研究的环氧乙烷水合制乙二醇反应精馏塔为例来验证所建立方法的有效性。该体系存在两个不可逆的连串竞争反应，如式(12)和式(13)所示。环氧乙烷（EO）首先与水反应生成乙二醇（EG），EG与EO可继续反应生成二乙二醇（DEG），其中EG 为中间产物，也是目标产物，DEG 为副产物。由于采用反应精馏技术可以显著提高目标产物EG 的选择性[11]，所以这是一个典型的以选择性为目标的反应精馏应用实例。

对于清代碑学发展的反思、批评的文章如戴逸[4]认为，“碑学派所说固然也抓住了帖学派的某些弱点，但门户之见太深。贬斥异己，一笔抹杀，未必公正。平心而论，北碑派未必都是好字，南帖派也未必都是劣书，北碑南帖各有特色。”黄惇[5]亦认为，金农、赵之谦的“稿书”融合碑帖，而杨守敬、沈曾植并不否定帖学，同时提出:“为什么刻帖滤漫、翻刻失真即当抛弃，而碑刻法漫、残破模糊，却当备加赞扬呢？”丛文俊[6]更是提出，“就连倡碑名家阮元，书法亦未能逾出主流帖学之外。”

这里说明，尽管有诸多文献研究了EG 反应精馏塔的设计问题[20-22]，但很少涉及到反应段塔板上反应体积分配的优化问题。为此，本文同文献[11]进行对比研究。文献[11]采用MINLP 法对反应精馏塔进行综合，包括对反应段各塔板上的反应体积进行优化。图3为文献[11]给出的塔示意图和部分设计参数（文献图2），表1同时给出了各反应塔板上的反应体积数据。为了方便比较，本文设计所采用的塔结构（塔板数和进料位置）和操作参数（塔压，进料流量）与图3相同，反应段总的反应体积也与文献相同。另外，本文设计规定EO 的转化率≥99.5%，产品中EG 的摩尔分数为0.95，EG 对EO 的选择性≥90%。需要说明的是，对于图3流程，如果规定了进料条件、EO 的转化率和EG 的选择性，意味着塔底产品流量和组成可直接通过系统的物料平衡关系确定，所以不能再规定其他条件（如EG 的组成）。基于以上指定，塔模拟时再沸器负荷将是唯一可调节变量。

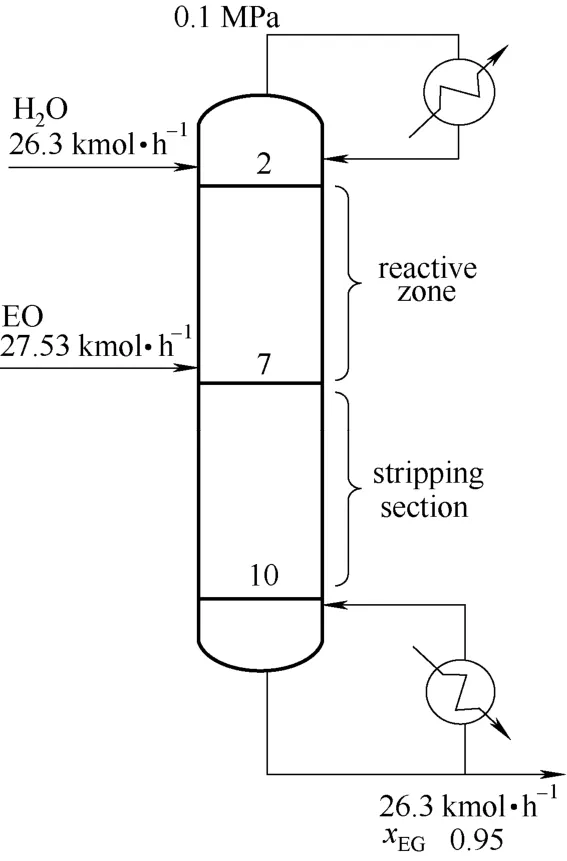
图3 EG 反应精馏塔示意图Fig.3 Schematic diagram of EG reactive distillation column

本文在Aspen Plus 软件平台上对塔进行模拟，采用的基本假设是：相平衡计算采用平衡级模型，其中气相假定为理想气体，液相活度系数用NRTL模型计算；计算涉及的所有物性参数均取自Aspen 软件数据库；模拟需要的反应动力学数据取自文 献[11]。在方法实施之前，对文献[11]的优化设计方案进行模拟重现。采用如图3给定的输入条件，同时选用文献[11]给出的反应段各塔板上的反应体积数据，指定与文献相同的塔底产品中EG 的摩尔流量（25 kmol·h-1，对于EG 的摩尔分数为0.95，对应的EG 的选择性为90.81%），由Aspen 软件模拟得到再沸器的负荷为6.97 MW，与文献给定的负荷6.9 MW 非常接近，相对误差约为1.0%。说明了本文模拟方法的可靠性和设计结果的可对比性。

将流程模拟技术和第1 节建立的㶲计算模型相结合，可进而计算反应塔板上㶲损失及其分布。具体过程为：首先，用Aspen Plus 软件对反应精馏塔进行模拟，得到每个塔板上各流股的温度、流量、各组分组成及所有组分物性参数信息；然后，根据建立的㶲计算模型[式(1)～式(9)]计算各流股的㶲及每个塔板的㶲损失分布。同时，为考察每个塔板上物理㶲损失与化学㶲损失对总㶲损失贡献的差异，本文对二者分别进行计算。对于本例，由于㶲计算涉及的焓、熵、相平衡常数等参数及其分布可直接通过商业软件模拟得到，这不仅方便于㶲的计算，同时能保证计算的准确性。

3.2 等反应体积分配设计

将文献[11]给出的总反应体积平均分配至反应段每块塔板上，即各个塔板的反应体积均按625 L进行模拟计算，结果见表1（base case）。此条件下塔再沸器的负荷为8.15 MW。

此条件下塔内㶲损失分布如图4所示。由图可见：①在EO 进料的第7 块塔板上化学㶲损失达到最大，并沿塔向上逐板减小，这是由于EO 进料处反应物浓度最高，反应速率最快，熵产生最大，过程不可逆程度和化学㶲损失也最大；②物理㶲损失与化学㶲损失分布具有相同规律，这是由于化学反应导致EO 进料板比相邻塔板上组分的浓度梯度和温度梯度更大（意味着该板上传质和传热推动力最大），这是导致过程不可逆性和㶲损失增大的主要原因；③反应塔板上物理㶲损失的数量级远远小于化学㶲损失的数量级，数值仅占后者的5%左右，这说明反应塔板上过程不可逆性和㶲损失主要由化学反应导致。这一结论揭示了反应精馏塔内部的能耗特征，对指导塔的优化设计具有重要意义。

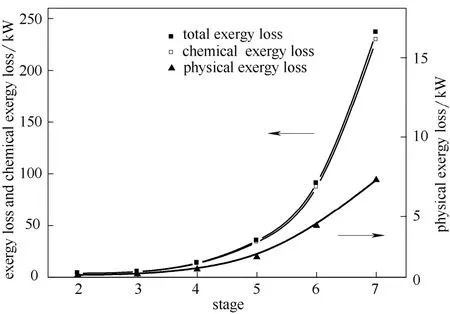
图4 反应段塔板上总㶲、物理㶲与化学㶲损失分布Fig.4 Profiles of total exergy,physical and chemical exergy loss along reactive section

3.3 反应体积分配的优化设计

在取得反应段塔板上㶲损失分布曲线及㶲损失原因分析的基础上，可根据2.2 节建立的调优方法，取不同的调优系数α对反应体积分布进行重新分配和逐步调优。表1中给出了A、B、C 和D 4种调优结果。从表1看出：①与等反应体积分布设计比较，调优后的4 个设计方案对应的再沸器负荷均有显著降低；②当逐步减小调优系数α的取值时，再沸器的负荷出现先减小后略增大的趋势，当α=0.94 时系统能耗最小，即方案C 为最佳方案，其能耗比等反应体积分配方案降低18.10%；③通过对该例反复调优，发现调优系数的取值对再沸器负荷的影响不显著，说明本文方法不需要复杂的计算和反复调优，便能取得优化的反应体积分布。另外，从能耗降低的比例分析，虽然通过反应体积分布的优化使再沸器的负荷得到降低，但再沸器的负荷或外界输入的能量仍在系统能耗中起主导作用。

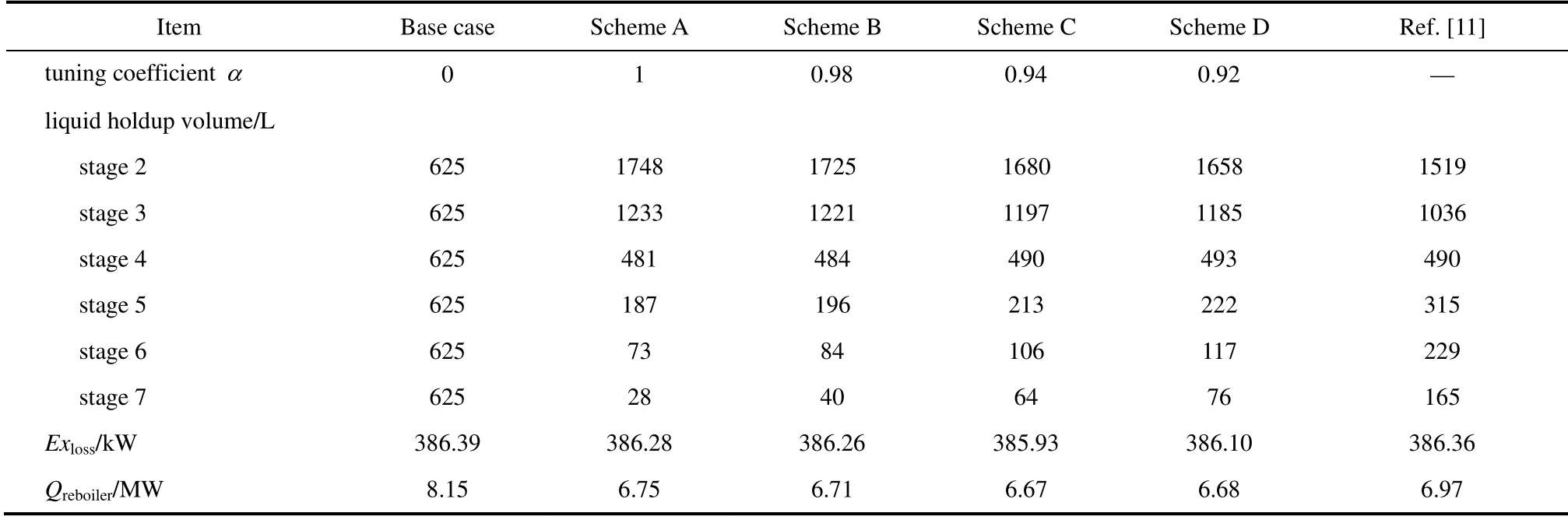
表1 不同反应体积分配方案的模拟结果及比较Table 1 Simulation results and comparison for different schemes of reaction volume distribution

图5给出了表1中5 种不同设计方案对应的反应段塔板上㶲损失分布。从中可见，等反应体积分布的设计将导致EO 进料板及相邻塔板上㶲损失急剧增大，进而增大总㶲损失及再沸器负荷；通过对反应段塔板上反应体积的分布进行优化，使㶲损失分布曲线变得平缓，塔板上总㶲损失显著降低，再沸器负荷也相应减小。由热力学第二定律分析，沿塔㶲损失分布曲线越平缓对应过程不可逆性越小，说明了本文设计和优化方法的合理性和有效性。

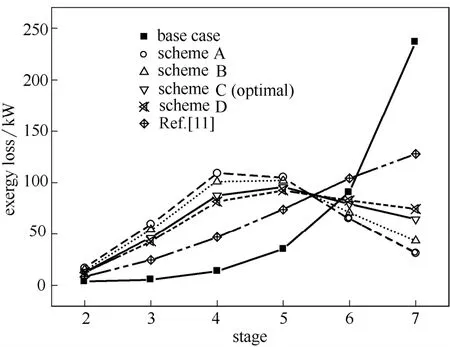
图5 不同设计方案对应的㶲损失分布比较Fig.5 Comparison of exergy loss profile between different designs

3.4 设计结果与文献结果对比

表1同时给出了本文优化设计结果和文献[11]结果的比较，其中文献[11]栏给出的再沸器负荷和㶲损失数据是本文软件的计算结果，即将文献给出的反应体积分布数据输入软件，规定塔底产品中EG的摩尔分数均为0.95，通过模拟得到再沸器负荷和㶲损失数据。从中看出，本文获得的最佳设计（方案C）与文献[11]给出的反应体积分配规律完全一致，并且再沸器负荷比文献结果降低约4.3%，总的㶲损失降低约0.1%。图5同时给出了文献[11]设计结果对应的㶲损失分布，从图看出，两种设计得到的㶲损失分布规律非常接近。通过以上对比说明，本文方法不仅能够实现反应精馏塔板上反应体积的优化设计，同时更深层次揭示了反应精馏塔内部能量损失的部位和原因，而文献的MINLP 法则不具备此优越性。这里还强调，虽然本文方法应用于具有不可逆连串竞争反应的反应精馏体系，但由于基于热力学第二定律的㶲损失分析方法对能量密集型过程的节能优化具有普遍指导意义，所以本文方法也可以拓展到以转化率为目标的可逆反应体系，这也是将来需要研究的重要课题。

4 结 论

针对以选择性为主要目标的反应精馏塔的节能优化问题，提出一种基于㶲损失分析的反应塔板上反应体积优化分配的设计方法，并以环氧乙烷水合制乙二醇反应精馏为例验证了方法的有效性。研究表明：（1）传统采用的等反应体积分配的设计方法将导致某些反应塔板上的㶲损失剧增，是导致能量利用不合理的重要因素，而通过本文建立的方法进行设计，可使系统能量利用更加合理、能耗更低；（2）反应塔板上物理㶲损失远远小于化学㶲损失，反应塔板上过程的不可逆性和㶲损失主要由化学反应导致，优化反应精馏过程的反应条件比优化分离条件更为重要；（3）相对于MINLP 等方法，本文方法的优点在于能够更深层次分析和揭示反应精馏塔内部能量损失的部位和原因，这将为反应精馏塔的工业化设计提供重要的理论依据和模型支持。

符 号 说 明

a——组分活度

cp——比热容，kJ·kmol-1·K-1

Ex——㶲，kJ

ExC——化学㶲，kJ

Exloss——㶲损失，kJ

ExPh——物理㶲，kJ

f——㶲损失比例系数

F——进料流量，kmol·s-1

G——Gibbs 自由能，kJ·kmol-1

H——焓，kJ·kmol-1

i——第i个组分

j——第j个塔板

k——第k个塔板

L——液相流量，kmol·s-1

Mj——第j个塔板反应体积，m3

Mt——反应段总反应体积，m3

nr——反应段总板数

p——压力，kPa

r——反应速率，kmol·m-3·s-1

S——熵，kJ·kmol-1·K-1

T——温度，K

V——汽相流量，kmol·s-1

x,y——组分摩尔分数

α——反应体积调优系数

β——等压膨胀系数，K-1

γ——相变焓，kJ·kmol-1

ξ——分子中原子的个数

[1]Malone M F,Doherty M F.Reactive distillation [J].Ind.Eng.Chem.Res.,2000,39:3953-3957

[2]Backhaus A A.Continuous processes for the manufacture of esters [P]:US,1400849.1921-12-20

[3]Harmsen G J.Reactive distillation:the front-runner of industrial processes intensification [J].Chemical Engineering and Processing,2007,46:774-780

[4]Jana A K,Mane A.Heat pump assisted reactive distillation:wide boiling mixture [J].AIChE Journal,2011,54 (11):3233-3237

[5]An Weizhong (安维中),Lin Zixin (林子昕),Jiang Yue (江月),Chen Fei (陈菲),Zhou Liming (周立明),Zhu Jianmin (朱建民).Design and optimization of an internally heat integrated reactive distillation column for ethylene glycol production [J].CIESC Journal(化工学报),2013,64 (12):4634-4640

[6]Sun Lanyi (孙兰义),Wang Rujun (王汝军),Li Jun (李军),Liu Xuenuan (刘雪暖).Simulation of reactive dividing wall column [J].Chemical Engineering(China) (化学工程),2011,39 (7):1-6

[7]Almeida-Rivera C P,Grievink J.Process design approach for reactive distillation based on economics,exergy,and responsiveness optimization [J].Ind.Eng.Chem.Res.,2008,47:51-65

[8]Okasinski M J,Doherty M F.Design method for kinetically controlled,staged reactive distillation columns [J].Ind.Eng.Chem.Res.,1998,37:2821-2834

[9]Almeida-Rivera C P,Swinkels P L J,Grievink J.Designing reactive distillation processes:present and future [J].Computers and Chemical Engineering,2004,28:1997-2020

[10]Chadda N,Malone M F,Doherty M F.Feasible products for kinetically controlled reactive distillation of ternary mixtures [J].AIChE Journal,2000,46 (5):923-936

[11]Ciric A R,Gu D.Synthesis of nonequilibrium reactive distillation processes by MINLP optimization [J].AIChE Journal,1994,40 (9):1479-1487

[12]Doherty M F,Malone M F.Conceptual Design of Distillation Systems [M].New York:McGraw-Hill Higher Education,2003:476-478

[13]Rant Z.Exergy,a new word for “technical work capacity” [J].Forsch Ing.Wes.,1956,3:22-36

[14]Wang Dongliang (王东亮),Feng Xiao (冯宵),Li Guangbo (李广播),Liu Yongjian (刘永健).Exergy calculation method based on flowsheeting simulation and its application [J].Computers and Applied Chemistry(计算机与应用化学),2012,29 (9):1069-1074

[15]Rivero R.Exergy simulation and optimization of adiabatic and diabatic binary distillation [J].Energy,2001,26:561-593

[16]Zheng Ying’e (郑英峨),Zhang Lianke (张联科).Chemical exergy and its applications in energy saving [J].Chemical Industry and Engineering(化学工业与工程),1985,2 (2):7-17

[17]Riekert L.The efficiency of energy-utilization in chemical processes [J].Chemical Engineering Science,1974,29 (7):1613-1620

[18]Szargut J.Chemical exergies of the elements [J].Applied Energy,1989,32 (4):269-286

[19]Feng Xiao (冯霄),Li Qinling (李勤凌).Principles and Technology of Energy Saving in Chemical Processes (化工节能原理与技术) [M].3rd ed.Beijing:Chemical Industry Press,2008:52-54

[20]Baur R,Higler A P,Taylor R,Krishna R.Comparison of equilibrium stage and non-equilibrium stage models for reactive distillation [J].Chemical Engineering Journal,1999,76:33-47

[21]Kumar A,Daoutidis P.Modeling,analysis and control of ethylene glycol reactive distillation column [J].AIChE J.,1999,45:51-68

[22]Ciric A R,Miao P.Steady state multiplicities in an ethylene glycol reactive distillation column [J].Ind.Eng.Chem.Res.,1994,33:2738-2748