基于AGMF和改进灰色关联度分析的柴油机故障诊断

付兴民，潘宏侠

（1.中北大学　机械与动力工程学院，太原030051；2.中国人民解放军66336部队，河北　高碑店074000）

基于AGMF和改进灰色关联度分析的柴油机故障诊断

付兴民1，2，潘宏侠1

（1.中北大学机械与动力工程学院，太原030051；2.中国人民解放军66336部队，河北高碑店074000）

针对柴油机实测振动信号易受噪声污染而淹没有用信息的问题，设计一种自适应广义形态滤波器（AGMF），通过梯度法自适应调权值，使降噪效果达到最优。提出改进的灰色关联度分析方法进行故障诊断。实验发现，经过形态滤波降噪后的振动信号，效果较好，提取时域频域的特征值作为特征向量进行故障判别，运用改进的灰色关联度分析方法能够准确的判断故障模式，从而验证所提方法的有效性。

声学；故障诊断；自适应广义形态滤波；改进灰色关联度分析

柴油机是最常见的往复式动力机械设备，是汽车、船舶、机车、工程机械、农业机械和矿山机械等设备的动力源，被广泛应用于工业、农业、工程、建筑、国防建设和交通运输等各个行业中，柴油机在国民经济和日常生产生活中发挥着重要作用。由于柴油机的结构复杂及工况恶劣造成其故障的多发性和多样性［1，2］，能及时发现和快速、有效诊断并排除故障是国内外学者研究的主要内容。

由于柴油机工作环境复杂恶劣，随机干扰较多［3］，在故障判别时首先要对信号进行降噪处理。数学形态学算法作为一种非线性信号分析处理方法，具有降低随机噪声干扰、有效剔除脉冲、提取信号冲击成分、有效提高信噪比等优点，被逐步应用到机械故障诊断中的振动信号处理方面，并且取得到了较好的效果［4］。根据数学形态学理论，设计一种基于梯度法的自适应调权值的广义形态滤波器，取得了较好的降噪效果。灰色关联分析是灰色系统理论的一个分支［5］，灰色关联分析最主要的工具是灰色关联度，它是用来衡量两序列之间的关联程度，弥补数理统计方法的缺陷，在系统分析、方案决策和综合评估等方面应用非常广泛。运用改进的灰色关联度分析法对故障模式进行判别，实验结果表明所提方法的有效性。

1　柴油机故障模拟实验

实验在柴油机试验台上进行，主要由柴油机（潍柴R6105AZLD）、减速箱、增速箱和涡流制动器等几个部分组成，如图1所示。数据采集通过传感器将物理信号转变为电压信号，经过电荷放大器，通过DASP系统将信号存储到计算机中。实验中，转速为1 200 r/min，采样频率为48 KHz，模拟6种工况进行分析，如表1所示。

图1　柴油机试验台

表1　柴油机工况模拟方案

柴油机的气缸结构及传感器的布置，如图2所示，图中1#-9#表示传感器以及传感器的位置，1-6表示6缸，1-8#传感器采用压电加速度传感器，9#采用电涡流转速传感器。6缸柴油机气缸的点火顺序为：1-5-3-6-2-4。

图2　柴油机的气缸结构及传感器的布置

2　基于梯度法自适应广义形态滤波的滤波降噪

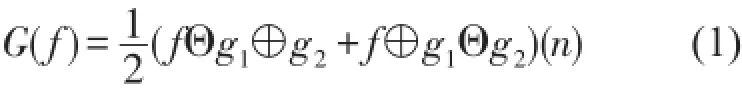
数学形态变换一般分为二值形态变换和灰值（多值）形态变换。实验中采集到的柴油机振动信号其中f表示振动信号，g1，g2表示结构元素，Θ表示腐蚀运算，⊕表示膨胀运算。由于是均值滤波器，其权系数固定值为0.5，权系数在滤波过程中保持不变。这样的话，滤波降噪效果就不能自适应达到最佳。为了使滤波效果达到最优，采用梯度法［9］确定权系数。

设柴油机原始信号x（n）=s（n）+i（n），n=0，1，…，N-1，s（n）为理想信号，i（n）为噪声。滤波器输出信号y（n），e（n）为误差信号，表示为e（n）=s（n）-y（n）。广义形态开、闭的输出为滤波器输出信号是一维离散的时间序列，其灰值形态变换包括腐蚀、膨胀、形态开和形态闭，以及形态开、闭的级联组合［6］。

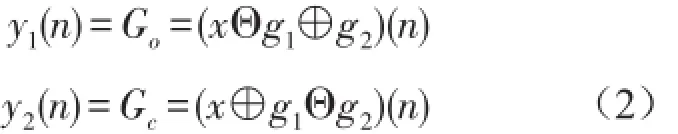
形态滤波器是基于信号的几何特征，利用预先定义的结构元素对信号进行匹配，从而达到提取信号、保持细节和抑制噪声的目的。常见的结构元素有直线型，三角形，半圆形，正弦形等等。其中，半圆形有利于降低随机噪声干扰。柴油机在运行过程中，随机噪声干扰严重，因此选择半圆形结构元素。根据Maragos的理论［7，8］，采用两个不同尺度的半圆形结构元素构建广义形态开和闭均值滤波器

其中ai（n）表示权系数。

若通过梯度法修正权系数，e2（n）对权系数的梯度定义为

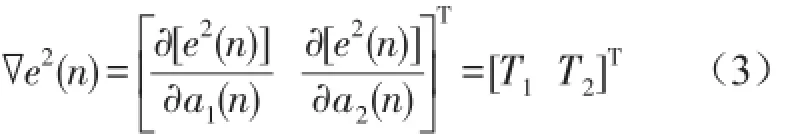
基于梯度法的自适应形态滤波迭代计算过程为：

①对原始信号x（n）作广义形态开和广义形态闭运算得到y1（n）、y2（n）。

②计算单个误差样本。

图3　原理图

其原理见下图。其中，上标k表示迭代次数，［e（n）］k为单个误差样本。

经过以上计算，选取两种半圆形的结构元素，宽度为：L1=3，L2=5，其对应的高度为：H1=2.75，H2=4.58。运用梯度法自适应调权值，求得系数a1=0.511 0，a2=0.489 0。以正常工况下的一个周期为例，经过自适应广义形态滤波前后的时域图如图4（a）（b）所示。对比两图发现，降噪后的信号峰值有所降低，信号平滑许多，信号变得系数，并且去除了一些随机噪声。

图4　降噪前后时域图

为了能更加直观的说明自适应广义形态滤波器的效果，将小波降噪、形态开和闭均值滤波与之进行对比。由文献［10］知，由于我们是实测信号，并不知道理想信号，评价降噪的指标只能由降噪后的信噪比SNR和均方根RMSE来衡量，一般的认为，SNR越大越好，RMSE越小越好。

信噪比是指原始信号能量与噪声能量的比值，记为SNR；降噪后信噪比是指降噪后的信号能量与噪声能量比。均方根误差RMSE体现原始信号和去噪之后信号之间的差异。

降噪效果对比如表2所示。可以看出，自适应形态滤波信噪比最大，均方根误差最小，比小波降噪要好得多。并且相比均值滤波要好，通过基于梯度法的自适应的调整权值，使滤波效果达到最佳。

3　基于改进灰色关联度分析故障诊断

20世纪80年代，邓聚龙教授提出灰色理论。灰色关联度分析是灰色理论中的重要分支，用来衡量两序列之间的的关联程度。灰色关联分析方法具有样本小，计算量小的优点，不会出现量化结果和定性分析结果不符的情况。在机械设备故障诊断领域中，灰色关联度分析是一种重要的模式识别方法。本文中，柴油机可以视作一个灰色系统，提取柴油机振动信号的各工况特征信息的参数值，作为各种工

表2　降噪方法的评价指标

对前文降噪后的信号，提取时域频域特征值作为特征向量，在每一种工况下取4个工作周期内信号的特征参数作为特征向量，为1个样本。取均方根值、峰值指标、脉冲指标、裕度指标、功率谱重心指标、均方频率、功率谱方差和谐波因子组成特征向量，得到标准模式特征向量和待检测模式特征向量两组特征向量。利用传统的邓氏关联度分析方法和改进灰色关联度分析法进行处理，并计算两组特征向量之间的关联度，结果如表3和表4所示，其中，G1-G6表示柴油机标准模式特征向量Xi，C1-C6表示待检测模式特征向量Yj。况下的标准模式向量，通过计算待检测特征分量与标准模式分量之间的关联度，并依据最大关联度原则，可以分析和判断待检测模式分量属于哪一种标准模式分量，从而可以推断出最大可能性的故障类型，实现对柴油机的故障模式识别。然而由传统的邓氏关联度模型［11］计算关联度时，计算方法中影响结果的因素很多，例如特征参数调整顺序、标准模式向量等，诊断结果往往不是很精确，甚至出现误判的情况，因此提出改进的灰色关联度分析方法［12］。主要原理是：采用中心化法对数据进行无量纲处理，并以距离分析法确定各指标的权值，从而求取关联度。其过程如下：

（1）采用中心法将原始数据进行无量纲处理，以期能将柴油机各工况的特征值差异性体现的最大化；

（2）确定理想样本；

（3）采用欧式距离公式，计算各样本点到参考样本点的距离；

（4）计算样本点到最优样本点的相对接近度；

（5）相对接近度的归一化处理；

对比分析两表，依据最大关联度的判据，可以判断每一种故障类型。表3中，C1和G1关联度最大，则为正常工况；C2和G2关联度最大，为单缸断油工况；C3和G3关联度最大，为双缸断油工况；C4和G5关联度最大，本应该和G4关联度最大，出现了误判；C5和G5关联度最大，为供油提前角增大工况；C6和G6关联度最大，为空气滤清器堵塞工况。而表4中，依据最大关联度判据，与实际的情况是一致的，验证了判断的准确性。其中表4的最大关联度值均比表3中最大关联度值要大，说明改进的灰色关联度分析可以提高故障诊断的精度。同时可以看出，对原始数据进行处理后，可以增大分析对象之间的差异性，提高分辨的效果。

表3　传统的邓氏关联度分析计算结果

表4　改进的灰色关联度分析计算结果

4　结语

（1）针对柴油机实测振动信号易受噪声污染而淹没有用信息的问题，研究一种基于梯度法的自适应调权值的广义形态滤波器，并且给出计算过程，通过梯度法自适应调权值，对柴油机实验实测信号进行降噪处理，对比其他方法发现，取得了较好的效果。

（2）根据灰色理论，提出改进的灰色关联度分析方法，并且给出计算过程，对降噪后的信号提取时域频域的特征值作为特征向量，利用改进灰色关联度分析法进行故障判别，并与传统的邓氏关联度分析进行对比，发现改进的灰色关联度分析方法能够提高精度，增大分析对象之间的差异性，实现精确判别，从而证明所提方法的有效性。

［1］曹龙汉.柴油机智能化故障诊断技术［M］.北京：国防工业出版社，2004.

［2］董安，潘宏侠.柴油机振动信号的分形特征及故障诊断［J］.噪声与振动控制，2014，34（2）：144-147.

［3］蔡艳平，李艾华，王涛，等.基于小波包和LMS自适应降噪的柴油机振动诊断［J］.噪声与振动控制，2011，31（1）：104-109.

［4］孙敬敬.数学形态学在振动信号处理中的应用研究［D］.保定：华北电力大学，2012.

［5］邓聚龙.灰理论基础［M］.武汉：华中科技大学出版社，2002.137-138.

［6］陈平，李庆民.基于数学形态学的数字滤波器设计与分析［J］.中国电机工程学报，2005，25（11）：60-65.

［7］Maragos P，Schafer R W.Morphological filters.Part I: Their set theoretic analysis and relation to liner shift invariant filters［J］.IEEE Transactions on ASSP，1987，35 （8）:1153-1169.

［8］Maragos P，Schafer RW.Morphological filters.Part II: Their relation to median，order-statistic，and stack filters［J］. IEEE Transactions onASSP，1987，35（8）:1153-1169.

［9］蒋章，邓艾东，蔡宾宏.基于梯度法的自适应广义形态滤波在碰摩声发射信号降噪中的应用［J］.中国电机工程学报，2011，31（8）：87-92.

［10］陶珂，朱建军.小波去噪质量评价方法的对比研究［J］.大地测量与地球动力学，2012，32（2）：128-133.

［11］周秀文.灰色关联度的研究与应用［D］.长春：吉林大学，2007.

［12］舒服华.改进灰色关联分析在铸造型砂品质评价中的应用［J］.铸造技术，2007，28（1）：15-18.

Diesel Engine Fault Diagnosis Based onAGMF and Improved Grey CorrelationAnalysis

FU Xing-min1，2，PAN Hong-xia1
（1.Mechanical and Power Engineering College，North University of China，Taiyuan 030051，China；2.Unit 66336 of P.L.A.，Gaobeidian 074000，Hebei China）

Viewing that the actual vibration signals of diesel engines could be easily contaminated and the useful information was often covered by noises，an adaptive generalized morphological filter（AGMF）was designed.The adaptive adjustment of the weights by gradient method enabled the optimal noise reduction.The improved grey correlation analysis was proposed for fault diagnosis.The results of the test show that the effect was good after denoising the vibration signal by the morphological filter.The eigenvalues in time and frequency domains were extracted as the feature vector for fault diagnosis.The improved grey correlation method could accurately judge the fault mode.So，the effectiveness of the proposed method was verified.

acoustics；fault diagnosis；adaptive generalized morphological filtering；improved grey correlation analysis

TH165+.3

ADOI编码：10.3969/j.issn.1006-1335.2015.05.031

1006-1355（2015）05-0150-04

2015－03－06

付兴民（1988－），男，山东禹城人，硕士研究生，主要研究方向为设备故障检测、诊断与控制，以及模式识别等。

E-mail:718143375@qq.com