基于小波包近似熵与LMS加权特征融合异步电机故障诊断

曾求洪，宾光富，李学军，罗　军

（湖南科技大学　机械设备健康维护湖南省重点实验室，湖南　湘潭411201）

基于小波包近似熵与LMS加权特征融合异步电机故障诊断

曾求洪，宾光富，李学军，罗军

（湖南科技大学机械设备健康维护湖南省重点实验室，湖南湘潭411201）

针对大多数情况下异步电机故障在不同传感器和转频等工况参数下的近似熵集合存在差异，难以有效提取表征不同故障状态的信号特征，进行故障状态识别的问题，提出一种基于小波近似熵与加权最小均方误差LMS的特征融合异步电机故障诊断方法。首先，通过小波包分解电机正常、转子不平衡、转子弯曲以及基座松动等故障信号，得到不同频带的信号特性，然后选取最优尺度提取不同频带上近似熵构成集合。然后，结合同种故障不同运行状态下的近似熵集合，通过采用自适应LMS算法进行加权融合提取电机不同故障状态的最优特征，将其作为SVM的输入进行故障分类，从而实现不同工况下故障状态的精确识别。最后，针对异步电机正常运行、转子不平衡、转子弯曲、基座松动四种运行状态，分别采用所提出的SVM分类法和BP神经网络法，结果表明SVM分类法比BP神经网络法的分类识别率更高，诊断效果更好。

振动与波；异步电机；小波包近似熵；最小均方误差；特征融合；SVM

异步电机是广泛应用于各工业领域的机械装置，然而由于零部件多、工作环境恶劣、安装连接方式特殊等，一旦发生故障难以有效进行诊断分析和及时的改进调整，给经济生产效益带来严重的损失，甚至潜在地威胁着工作人员的生命安全，因此能对电机故障的检测诊断，保证其安全高效的运行具有重大的意义［1-3］。异步电机故障的高效准确识别和早期预报的可靠性关键在于故障信号特征提取［4］。国内外专家学者对电机开展了深入的研究，目前常用的方法有：时频特征参量提取法，该方法对样本量较小的非线性较强的振动故障信号特征提取有一定优势［5］；自适应的方法，对强噪声背景下的故障信号具有很强抗干扰性和自适应性［6］；刘金朝等［7］提出自适应共振解调法，避免带通滤波器难以选择的困难，实现滚动轴承的故障诊断。

针对大多数情况下异步电机故障在不同传感器和转频等工况参数下的近似熵集合存在差异，难以有效提取表征不同故障状态的信号特征，进行故障状态识别的问题，充分结合小波包变换的特点，对小波包分解后各独立频带信号分量用近似熵值来量化故障特征，可以反映不同故障的不规则性和复杂性。故采用多尺度小波包近似熵对电机故障信号进行多尺度近似熵提取构成同种状态近似熵集合［8-11］；而同种故障不同传感器和转频下的近似熵集合存在着较大的差异，即同类故障的类内距离变大进而弱化异类故障之间的距离，不便于特征的完整和有效提取。本文进一步引入加权LMS（Least Mean Square）算法思想对同种故障的所有近似熵集合各自加权自适应的融合，使得电机故障的特征提取更加有效和完整，最后采用SVM（Support Vector Machine）分类器［12］实现对电机正常、电机转子不平衡、转子弯曲和基座松动四种故障识别。实验证明：该方法对故障数据源进行了完整及有效的特征提取，识别率更高。

1　小波包与小波包近似熵

1.1小波包

针对小波分析在微弱、非平稳高频信号部分分解重构乏力的不足，采用小波包对信号进行分解重构.充分利用多分辨分解更为精细的分解方法，自适应的选择相对应的频带和信号频谱相匹配满足信号特性分析的需求。设定滤波系数是，令，可以定义递归函数

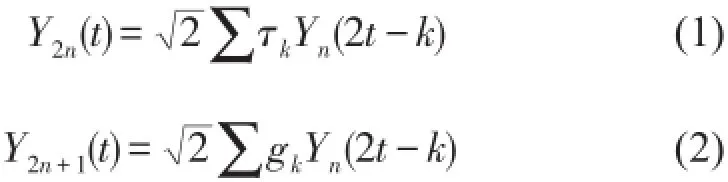
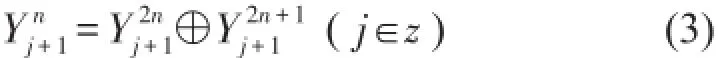
1.2小波包近似熵

近似熵用以定量描述时间序列的重复性，时间序列越复杂对应的近似熵越大，信号越趋于非平稳状态，系统越复杂，包含频率成分越丰富。设给定的时间序列为，预先给定模式维数m和相似容限r的值，则近似熵步骤为：

（1）按序列号连续顺序组成一组m维矢量X（）

i，即

其中i=1～N-m+1

（2）求出矢量X（i）与其余矢量X（j）之间的距离，这个距离为矢量X（i）与其余矢量X（j）对应元素中差的绝对值最大的一个，也就是

（3）针对每一个i值，按照即定的阀值r（r＞0），统计的数目及此数目与总的矢量个数的比值，可以记做，即

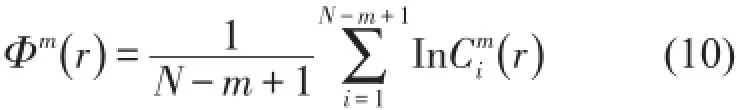
（6）输出此序列的近似熵值ApEn（m，r）为

此极限值以概率1存在，但在实际中N值不可能为∞，当N能取到有限值时，按上面所述的步骤求出的是序列长度为N时近似熵值Ap En的估计值，记做

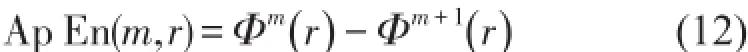
Ap En（m，r）显然是与m，r的取值有关的，通常取m=2，r=0.1～0.25 SD（u）（SD表示序列｛u（i）｝的标准差）。

2　加权LMS算法

难以获得传统数据融合中传感器方差参数，观测误差统计特性也不容易确定和实时变化，采用自适应算法中的最小均方误差算法（LMS），其对实现不同运行环境下多传感器故障特征融合具有独特的优势。该方法假设同一状态下有n个传感器T1，T2，∙∙∙，Tn，各个传感器的测量数据分别是x1，x2，∙∙∙，xn，方差分别是σ1，σ2，∙∙∙，σn，w1，w2，∙∙∙，wn分别是各个传感器的权重值［13，14］。设第p个传感器的第i个时刻数值是xp（i），则数据融合的状态估计值和权重条件是

设等权值是w，公式（13）可知w=1/n，通过局部融合状态估计值为

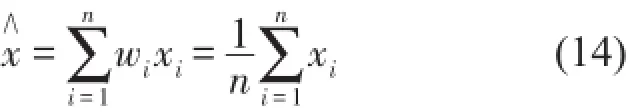
总均方误差是

由式（15）可知，总均方误差是关于加权因子的多元二次函数，进而可知总均方误差必定会存在最小值，根据数学方程拉格朗日极值求法构造函数

求解可知总均差最小时的加权因子是

传感器方差求取式

总均方误差为

因为x1，x2，∙∙∙，xn相对独立，且都是x的无偏估计，由p=q可知

因此对应的总均方误差为

3　数据采样和处理

3.1振动数据采集

异步电机故障实验以美国Spectra Quest公司的机械故障综合实验台为载体，针对Marathon公司的三相变频异步电机，标准电压是380 V，标准功率2.2 kW。采用美国PCB 608A11振动加速度传感器和丹麦B&K公司推出的PULE数据采集系统对三相变频异步电机进行传感器布置测点和故障数据采集，采样频率是8 192，如图1所示。在转频不同（分别为10 Hz、20 Hz、30 Hz、40 Hz和50 Hz）情况下，采集时间t=10s正常电机、转子不平衡、转子弯曲和基座松动四种状态，左右两端横向、纵向、径向三个方位，6个加速度传感器，共120组信号（120=4×2×3×5）的诊断数据N1、N2、N3、N4，作为原始的故障数据样本。

图1　电机故障模拟实验及数据采集

3.2数据分析处理

以异步电机转子不平衡为例，阐述对故障数据N2的分析和处理：先对转子不平衡数据进行预处理，五种转频的前60 000个数据点训练样本如图2所示。

异步电机故障诊断流程如图3所示，包括如下步骤：

（1）在一定采样频率下，实验采集故障振动信号有电机正常、转子不平衡、转子弯曲和基座松动四种状态的故障信号，各4 N组。

（2）选用函数wpcoef，采用“db 2”对某故障单一通道和单一转速的故障数据，用3层多尺度得到8个不同的独立频带，再对各个频带进行特征提取。

（3）对不同频带进行Ap Eni（i=1，∙∙∙，M）特征提取，进一步构成最优尺度近似熵集合Ap En。

（4）在不同转速和传感器下，对同一故障的最优尺度近似熵集合Ap En进行LMS算法加权融合，以此提取故障信息最佳融合特征，形成故障特征向量。

（5）建立SVM（SVM1、SVM2、SVM3、SVM4）组成的故障分类器，将4种故障特征向量输入SVM分类器，对特征向量进行训练学习。

（6）采集实时的电机故障数据，同样进行步骤（2）—（4），将测试样本形成的故障特征向量输入到SVM分类器中，确定异步电机故障类别。

图2　同一故障不同转频故障数据集合

图3　基于小波近似熵与LMS加权的特征融合故障诊断方法

对训练样本的每一列划分成若干小矩阵，然后进行小波包分解与重构，消除故障冗余信息和防止信息疏漏选取，针对每一个重构信号进行特征提取，近似熵构成了单状态的近似熵特征集合，以此类推获取其它五个的近似熵（近似熵值取四位有效数字）集合。

由表1可以看出不同的故障特征呈现出不同的分布特征，同种故障各个状态类内间的差距比较大而弱化了异类故障的类间距离，不利于进行特征提取。

针对这一实际情况，为了获得故障近似熵集合的最优融合，进一步实现故障特征完整有效的提取，引入LMS算法加权的思想，应用类内的近似熵集合实现最优融合，以此达到类内距离变小而类间距离放大化的目的。由公式（15）求的总均方误差确定权值，调节不同的提取特征，最终实现故障特征的最佳融合，为故障识别提供足够和充分的准备。图4和图5分别是不平衡故障特征自适应算法图像和不平衡情况下两组故障特征加权自适应算法融合图像。

图4　两组转子不平衡故障信息LMS融合

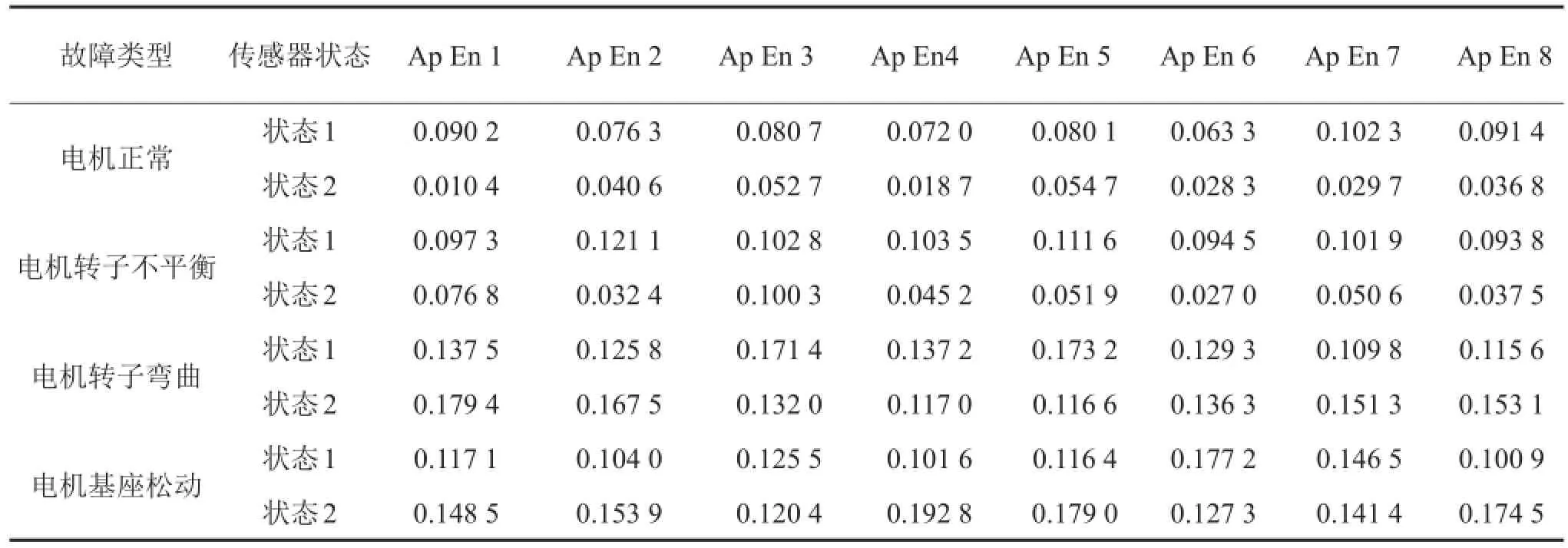
表1　电机四种故障状态的部分近似熵

绿色代表故障近似熵集合的预期输出，红色代表LMS算法输出，从图4可以看出通过自适应近似熵融合的特征向量，差异比较大，融合效果不理想；图5是自适应LMS算法加权融合近似熵的特征向量，由计算可知两组信号的融合权值分别是k=1、k= 0.4，两组信号差异小，融合效果好。以此类推将电机同一故障的多个状态近似熵集合进行自适应LMS算法加权处理，进一步对电机故障特征进行整合和提取。图6—图9分别是通过自适应LMS算法加权信息最佳融合之后的部分特征向量。

从图6—图9可以看出不同类型的故障经过多尺度近似熵集合和LMS算法加权融合处理之后，实现了最佳的特征近似熵集合特征融合，融合特征向量

特征各不相同。说明电机故障最佳融合特征向量作为SVM分类器的输入量是切实可行的。

图5　两组转子不平衡故障信息加权LMS融合

图6　正常状态最佳融合部分特征向量

图7　电机转子不平衡最佳融合部分特征向量

图8　电机转子弯曲最佳融合部分特征向量

图9　电机基座松动最佳融合部分特征向量

4　故障识别

在实验过程中选取60组、30组故障数据分别作为训练样本和测试样本，属于小样本情况。针对异步电机正常、电机转子不平衡、电机转子弯曲、基座松动四种运行工况，分别采用BP神经网络和SVM方法对电机故障进行识别，结果如表2所示。其中采用BP神经网络的诊断准确率分别是86.6%、80%、90%和76.6%，而采用本文所提出的SVM方法的诊断准确率分别是96.6%、93.3%、96.6%和90%。针对这四种运行工况，分别应用BP神经网络和SVM两种分类算法进行故障识别的平均值为83.3%和94.2%。因此，从识别结果可知，采用本文所提出的SVM作为分类器的故障识别精度比BP神经网络要好。

综合对比，针对异步电机故障在不同传感器和转频等工况参数下的近似熵集合存在差异，难以有效提取表征不同故障状态的信号特征，进行故障状态识别的问题，采用多尺度小波包近似熵的方法对电机故障信息进行第一步特征提取，结果发现同种故障不同传感器和转频的近似熵存在着较大的差异，即类内距离变大进而弱化异类故障之间的距离，给特征的完整和有效提取带来了难度。故进一步引入自适应LMS算法加权的思想，对同种故障不同状态的近似熵集合进行加权自适应的融合，最终实现电机故障的特征最优融合。最后通过BP神经网络和SVM方法对最优融合特征分类识别，分析比较证明SVM方法能对四种状态进行识别，识别率高，效果良好。

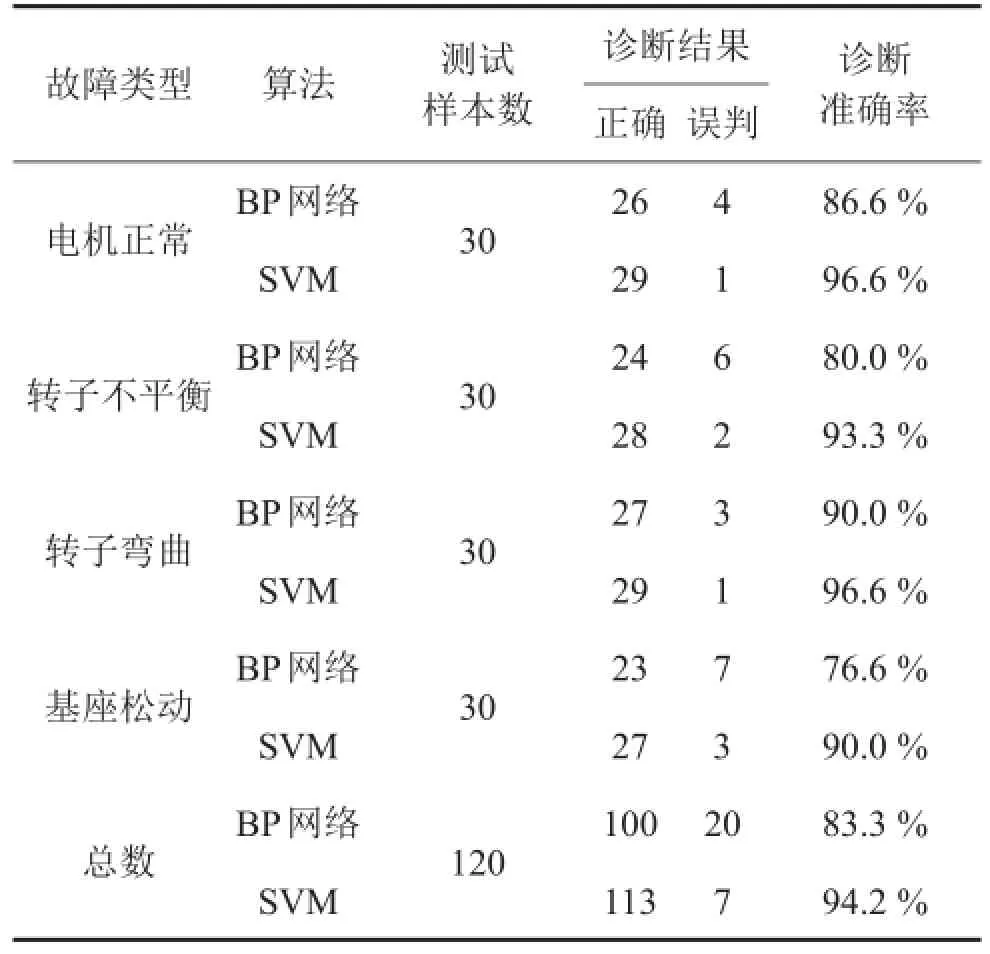
表2　 BP神经网络和SVM方法准确率分析对比

5　结语

（1）提出基于小波近似熵与LMS加权的特征融合异步电机故障诊断方法，针对传统时频特性方法难以挖掘异步电机故障非线性信号特征的问题，对故障信号进行多尺度、多分辨率分解提取近似熵，突出了原始信号的局部特征信息，能有效对故障特征进行提取；

（2）为了进一步对近似熵集合进行最佳特征融合以便于故障识别，针对同种故障不同状态的近似熵集合类内距离差异大，而弱化故障类间的距离不利于故障识别，引入自适应加权思想，将同种故障所有状态近似熵集合进行加权LMS方法的处理，进一步实现故障特征最优融合；

（3）分别采用BP神经网络和SVM法对四种故障状态进行识别诊断，实验结果表明：SVM分类法比BP神经网络法更能有效的对异步电机正常运行、转子不平衡、转子弯曲、基座松动四种状态进行分类识别，诊断率更高。

［1］IAS Motor Reliability Working Group.Report of large motor reliability survey of industrialand commercial installations，part I-II［J］.IEEE Transactions on Industry Applications，1985，21（4）:853-872.

［2］IAS Motor Reliability Working Group.Report of large motor reliability survey of industrial and commercial installations，part III［J］.IEEE Transactions on Industry Applications，1987，23（1）:153-158.

［3］Thorsen O V，Dalva M.A survey of faults on induction motors in offshore oil industry，petrochemical industry，gas terminals，and oil refineries［J］.IEEE Transactions on IndustryApplications，1995，31（5）:1186-1196.

［4］马宏忠，电机状态监测与故障诊断［M］.北京：机械工程出版社，2008.296-310.

［5］李平，李学军，蒋玲莉.基于KPCA和PSOSVM的异步电机故障诊断［J］.振动、测试与诊断，2014，34（4）：616-620.

［6］李天云，李光，杨春玲.基于自适应随机共振的异步电动机转子断条故障检测［J］.中国电机工程学报，2007，27 （15）：88-92.

［7］刘金朝，丁夏完.自适应共振解调法及其在滚动轴承故障诊断中的应用［J］.振动与冲击，2007，26（1）：38-41.

［8］何正友，蔡玉梅.小波熵理论及其在电力系统故障检测中的应用研究［J］.中国电机工程学报，2005，22（5）：38-43.

［9］Rosso O A，Blanco S.Wavelet entropy:a new tool for analysis of short duration branin electrical signals［J］. Joumal of Neurose Science Methods，2001，105:65-75.

［10］赵晶晶，杨燕，李天瑞，等.基于近似熵及EMD的高铁故障诊断［J］.计算机科学，2014，41（1）：91-94.

［11］Pincus S M.Approximate entropy as a measure of system complexity［J］.Proc National Academy Sciences，1991，88（6）:2297-2301.

［12］邹龙庆，陈桂娟.基于LMD样本熵与SVM的往复压缩机故障诊断方法［J］.噪声与振动控制，2014，34（6）：174-177.

［13］蔡艳平，李艾华，王涛.基于小波包和LMS自适应降噪的柴油机振动诊断［J］.噪声与振动控制，2010，30（1）：104-109.

［14］刘效武，王慧强，梁颖.基于异质多传感器融合的网络安全态势感知模型［J］.计算机科学，2008，35（8）：69-73.

Asynchronous Motor Fault Diagnosis Based on Wavelet Packet Approximate Entropy and Weighted LMS

ZENG Qiu-hong，BIN Guang-fu，LI Xue-jun，LUOJun
（Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment，Hunan University of Science and Technology，Xiangtan 411201，Hunan China）

The approximate entropy set of asynchronous motor faults is usually different under different condition parameters such as sensors type and switch frequency etc.So，it is difficult to effectively extract the signal characteristics for different faults in fault identification.In this paper，a feature fusion fault diagnosis method for asynchronous motors based on wavelet approximate entropy and weighted least mean square（LMS）error was proposed.First of all，through wavelet packet decomposition of the signals such as normal motor，rotor unbalance，rotor deflection，rotor and pedestal looseness etc.，the signal features in different frequency bands were obtained.Then，the optimal scale was chosen and the approximate entropy in different frequency bands was extracted to form a set.And the approximate entropy collections of the same fault but different operation conditions were combined.Using the adaptive LMS algorithm with weighted fusion，the motor optimal characteristics of different fault state were extracted.Using the fault characteristic as the input of the SVM，the faults were classified so that the precise identification of fault state under different working conditions was realized.Finally，considering four kinds of operation states:the normal operation of asynchronous motor，rotor unbalance，rotor bending and pedestal looseness，the proposed SVM classification method and BP neural network were applied respectively to the fault identification.The results show that the SVM classification has better recognition rate and higher accuracy than the BP neural network classification.

vibration and wave；asynchronous motor；approximate entropy of wavelet packet；least mean square error；characteristics fusion；SVM

TM343.2；TH165.3

ADOI编码：10.3969/j.issn.1006-1335.2015.05.029

1006-1355（2015）05-0139-06

2015－01－29

国家自然科学基金项目（51215121；51375162）

曾求洪，男，湖南娄底人，研究生，研究方向：机械设备故障诊断。

E-mail:1248579609@qq.com

宾光富，男，湖南衡山人，博士，副教授。研究方向：机械故障诊断。

E-mail:abin811025@163.com