基于遗传算法汽车动力总成悬置系统解耦优化

伍建伟，刘夫云，李　峤，周洪威，李应弟

（桂林电子科技大学　机电工程学院，广西　桂林541004）

基于遗传算法汽车动力总成悬置系统解耦优化

伍建伟，刘夫云，李峤，周洪威，李应弟

（桂林电子科技大学机电工程学院，广西桂林541004）

为避免传统优化算法在对汽车动力总成悬置系统优化中陷入局部最优解，采用遗传算法对其进行优化。在深入分析设计变量选取、约束函数的提取及目标函数的选取原则基础上，以悬置刚度为优化变量、固有频率的范围和固有频率之差为约束函数、六自由度方向的解耦率为目标函数，利用MATLAB平台的遗传算法进行优化。开发基于遗传算法汽车动力总成悬置系统解耦优化系统，并对某型号汽车动力总成系统优化。优化结果表明：系统的固有频率的分配和解耦率得到极大的改善，效率和精度都得到很大的提升。

振动与波；动力总成；悬置系统；遗传算法；优化；MATLAB

汽车动力总成的振动是汽车振动的主要激振源之一，对汽车NVH特性有很大的影响。设计合理的动力总成悬置系统［1-3］可以减少振动传递，提高乘坐舒适性。通过优化悬置刚度、悬置的位置和悬置的倾角来减小汽车动力总成系统向车架的振动传递。目前，大多采用的是传统的优化算法（梯度法、变尺度法、复合形法等），而汽车动力总成悬置系统能量法解耦的数学模型和悬置参数与解耦程度之间的关系复杂，极易限入局部最优解。

遗传算法［4-6］具有很强的适用性，能很好的解决工程实际中所遇到的问题，具有极强的全局寻优能力。同时随着MATLAB软件的升级和函数的优化，遗传算法函数ga在适用性、可靠性及稳定性等方面，都有很大的提高和改善。对于传统遗传算法求解不太好解决的问题，如大海捞针问题［7］、Schaffer函数最大值问题［8］、Ackley函数的最大值问题［9］，ga函数求解起来也都变得十分有效。正因如此，成为本文汽车动力总成悬置系统进行优化的首选算法。

本文在建立汽车动力总成悬置系统模型的基础上，对设计变量、约束函数、目标函数选取的原则展开深入的分析，然后利用遗传算法对系统进行解耦优化。考虑在ADAMS中进行优化存在很多不便［10］，因此利用MATLAB程序开发了基于遗传算法汽车动力总成悬置系统解耦优化系统。

1　汽车动力总成悬置系统

1.1汽车动力总成悬置系统模型

以动力总成四点悬置系统为研究对象，其动力学模型如图1所示。将动力总成视为6自由度的刚体，悬置视为具有三向刚度的弹性阻尼元件［1］。

图1　动力总成悬置系统动力学模型

为便于分析，在该模型上建立三个坐标系，分别为动力总成坐标系（G0-XYZ）、动坐标系（G0-xyz）和悬置系统坐标系（e-uvw）。动力总成坐标系的原点G0位于动力总成静平衡的质心位置，X轴与曲轴方向平行，指向发动机缸体前端面，Z平行于汽缸中心线，正方向指向气缸盖，Y轴由右手法则确定。动坐标系固结在动力总成质心处，当动力总成静止时，两坐标系相互重合。系统的广义坐标定义为：G0-xyz相对于G0-XYZ的坐标（平动与转动），即图2为橡胶悬置力学模型，坐标系的弹性主轴方向为其坐标轴方向。由于安装位置和角度的关系，悬置坐标系与广义坐标系不一致，故需组建式（3）的位置转移矩阵B和方向余弦矩阵T［11］。

1.2动力总成悬置系统动力学方程

在不考虑外力及阻尼作用下，动力总成悬置系统振动微分方程为

其中M为系统质量矩阵，K为系统刚度矩阵，q为广义坐标列阵，q¨为广义加速度列阵，转动惯量和惯量积的参考坐标系为G0-XYZ。

图2　橡胶悬置动力学模型

2　能量法解耦

通常的动力总成悬置系统的六个刚体模态之间存在不同程度的耦合作用，即耦合振动中的某一模态受到激发的同时，其它模态振动也受到激发。耦合作用不仅使系统的激振频带加宽，给隔振和频率配置带来困难。用某一自由度方向的动能占某一阶振动模态总动能的百分比作为模态解耦的评价指标，即能量法解耦［12，13］。

根据式（1）即可求得固有频率ωi（i=1，...，6）及振型矩阵Φ，由此便可求得系统各阶主振动时的能量分布，将它写成矩阵的形式，即为能量分布矩阵。

当系统作i阶主振动时的最大动能为

展开得

mkl表示质量矩阵的第k行、第l列元素，（ϕi）k和（ϕi）l分别表示振型（ϕi）的第k、l个元素。

第k个广义坐标在第i阶主振动最大动能所占的百分比为

如果Tp（k，i）=100%，则意味着第i阶主振型能量全部集中在第k个广义坐标上，其余广义坐标分配到的能量均为零，即该阶模态对应的主振动没有耦合性。

尽管能量法解耦具有一定的局限性［14］，但其在工程应用中已经成熟，仍具有很强的工程应用价值。在合理的刚度下提高动力总成悬置系统的解耦率和改善固有频率的配置仍然是优化设计的目标。

3　基于遗传算法汽车动力总成悬置系统解耦优化

由于文献［10］采用的是遍历算法，求解效率低。本文是其工作的继续，目的是提高该系统的求解效率及求解精度。对此，深入分析汽车动力总成悬置系统设计变量、约束函数、目标函数的选择原则的基础上，利用遗传算法求解。

3.1动力总成悬置系统的参数

以康明斯某型号的发动机为例，动力总成的总质量为1 111.6 kg。表1为动力总成系统在G0-XYZ坐标系下的转动惯量和惯性积。表2为悬置点在G0-XYZ坐标系下的坐标。其中，前左和后左悬置点主轴坐标系方位相对于G0-XYZ坐标系绕X轴正方向转过30°，前右和后右悬置点主轴坐标系方位相对于G0-XYZ坐标系绕X轴负方向转过30°。表3为悬置元件优化前的主轴静刚度，其动刚度系数为1.5。采用对称布置，故前左和前右、后左和后右悬置元件的刚度相同。

3.2优化前动力总成悬置系统的振动分析

优化前动力总成悬置系统的固有频率和能量分布，如表4所示。表中可以看出，优化前动力总成悬置系统尽管固有频率分配得比较合理，但沿y轴的平

表1　动力总成系统的转动惯量和惯性积/kg·m2

表2　悬置点相对G0-XYZ坐标系的坐标/mm

表3　优化前悬置元件的主轴静刚度/（N/mm）

动、绕x轴的转动和绕z轴的转动解耦率较低，最低的为54%，即这几个方向存在着严重的振动耦合。因此，需要对该系统进行优化改进。

3.3遗传算法优化

3.3.1数学模型

数学模型实质是联系设计变量与目标之间的纽带，是进行优化的前提条件。本文模型已经开发成动力总成悬置解耦优化系统，其求解结果经过了与ADAMS进行反复的对比，结果一致，验证了模型的正确性。目前，该系统已在东风柳州汽车有限公司得到推广和使用。因此，优化的前提条件已经满足。

3.3.2设计变量

设计变量是指在优化的过程中需要进行调整或者是可以改变的设计参数。将模型中可以改变且符合实际要求的量提取出来，作为设计变量，通过设计变量的变化使目标得到改善。理论上，增加设计变量的个数会使目标进一步的优化，但设计变量的增加会使得模型变得更为复杂，优化求解的效率大幅度下降。

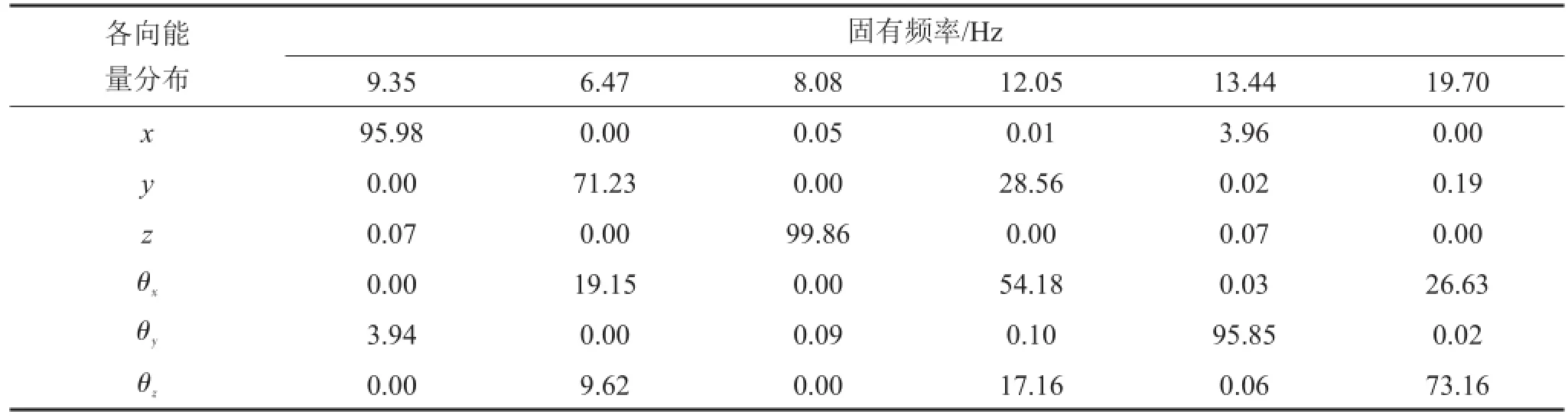
表4　优化前动力总成系统的固有频率和能量分布

动力总成系统的质量和转动惯量参数由厂家所提供，属于该型号的固有参数。同时，受到汽车总体布局的限制，悬置点的安装位置和安装角度也难以改变，能改变的参数往往是悬置点的主轴刚度。因此，设计方案选用悬置点的主轴静刚度作为设计变量。

3.3.3目标函数

目标函数也称适应度函数，目标函数实质上是指通过所建立的模型，最终所要达到的目标。因此，可以根据实际问题来选择目标函数，也可以通过优化的思维转化成目标函数。汽车动力总成悬置系统的目标是：最大程度地提高6个方向上的解耦率。如果分别将6个方向的解耦率作为目标函数，就会形成多目标优化问题，加大问题的复杂性。对此，利用加权系数法将其转化成单目标优化问题。

目标函数设计成如下的形式

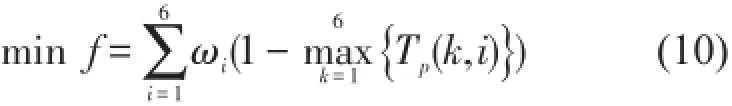
其中ωi表示权重系数，考虑到各个方向的解耦率是同一量级也近乎同等重要，因此，可令ωi=1。故目标函数简化为

由式（11）可知，当各个方向的解耦率均为100%时，该目标函数将达到最小值0。遗传算法寻优的过程中，f取得最小值时，解耦率最高。

3.3.4约束条件

将数学模型中所有的限制条件，提取出来建立线性或非线性约束函数，这就需要编程人员能清晰地知道模型中所有的限制条件。动力总成悬置系统的各个悬置点主轴静刚度的范围、各个方向固有频率的范围以及各个方向的固有频率差，均属于对模型的限制条件，因此都要将其编入约束函数中。各个约束条件具体的限制范围为：

（1）动力总成的固有频率通常可确定在5～18 Hz之间，以避开整车其他部分的固有频率和其他激振引起的共振固有频率。

（2）各个方向固有频率的限制，如表5所示。

（3）各个方向上固有频率差的限制。考虑到动力总成振动主要集中的z向和θx向，需要保证z向和θx向的频率差大于1 Hz，并且还要保证这两个方向及其他四个方向相互之间的频率差不小于0.5 Hz，避免各方向的振动耦合。

（4）各悬置点刚度的上下限也属于限制条件，也需要加入到约束函数中。综合考虑各悬置制造、安装等要求，主轴静刚度的范围设定为：100～1 000（N/mm）。

表5　动力总成系统固有频率的配置

此外，为了更加符合工程实际的要求，如果还有更为苛刻的条件，均可一并加入到约束函数中。

3.3.5遗传算法优化

确定设计变量、建立目标函数和提取约束函数后，通过调用MATLAB遗传算法函数ga，即可求得给定迭代代数和初始种群个数下的最优解。本文将迭代代数和种群个数均设置为500下求得最优解。

3.4遗传算法优化后动力总成悬置系统分析

表6为遗传算法优化后所得到的静刚度。为了满足工程实际要求，将刚度圆整到整数的十位，如表7所示。目标函数f=0.230 9（圆整前），f=0.233 5（圆整后），可以看出刚度圆整前后，目标函数值变化很小，说明系统的解耦率变化也很小。表8为遗传算法优化后动力总成的固有频率和解耦率。表9为优化后MATLAB与ADAMS计算的固有频率对比。其中，表8和表9均是圆整后的刚度所计算出的结果。

一般来说，某阶模态的解耦率达到85%，则认为是基本解除耦合，达到90%，即可认为是完全解耦。从表8可以看出，悬置主轴静刚度均在设定范围内、各个方向固有频率及其频率差分配合理（圆整后，第6阶固有频率稍稍高于固有频率的取值范围，但偏差很小可以忽略），并且优化后系统各个方向的解耦率均在90%以上，其中，x、z、及θz方向的解耦率均达到了99%，说明在此悬置刚度方案下，系统完全解耦。

从表9中可以看出由MATLAB开发软件求解与ADAMS计算的结果几乎完全相同，再次验证了该模型的正确性。考虑到计算效率在一定程度上受到计算机配置上的限制，大多文献也并未提及优化所耗时间。本文进行优化的计算机配置如下：Win 7系统、英特尔Xeon（至强）W3503双核处理器、内存2GB、MATLAB R2012 a版本。遗传算法优化耗时约1 159 s。较文献［10］需要两天才能得到的优化结果，效率和精度上都有很大的提高。

表6　优化后悬置元件的主轴静刚度（N/mm）

表7　优化后悬置元件圆整的主轴静刚度（N/mm）

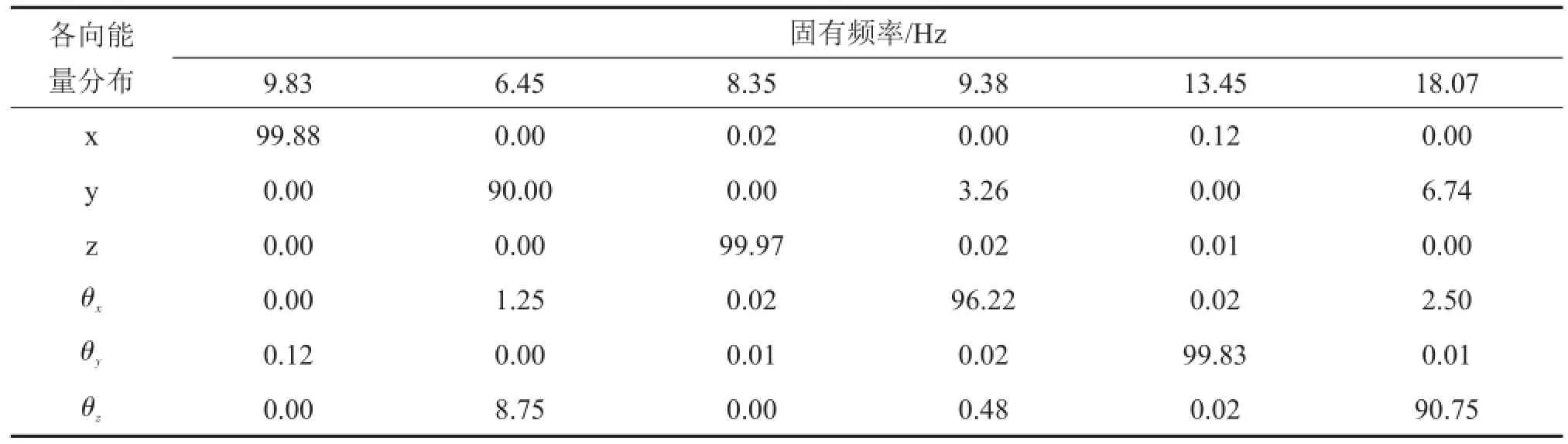
表8　遗传算法优化后系统的固有频率和能量分布

表9　优化后MATLAB与ADAMS求解的系统固有频率对比

另外，利用ADAMS来验证时，只是将所优化结果直接输入到模型中，因此，计算速度很快。

4　结语

对汽车动力总成悬置系统展开了深入的研究，采用能量对其进行解耦，在MATLAB平台开发了程序系统，即基于遗传算法汽车动力总成悬置系统解耦优化系统。利用该系统对某型号动力总成系统进行优化，结果表明：与前期工作（文献［10］）使用遍历算法优化相比，求解精度和效率有很大的提高。

［1］吕振华，范让林.动力总成—悬置系统振动解耦设计方法［J］.机械工程学报，2005，41（4）：49-54.

［2］吕兆平.能量法解耦在动力总成悬置系统优化设计中的运用［J］.汽车工程，2008，30（6）：523-526.

［3］李令兵，陈剑，吴赵生.基于ADAMS的发动机悬置系统设计［J］.噪声与振动控制，2007，27（6）：42-44+48.

［4］Holland J H.Adaptation in natural and artificial systems: An introductory analysis with applications to biology，control，and artificial intelligence［M］.Michigan Press，1975.

［5］Goldberg D E，Others.Genetic algorithms in search，optimization，and machine learning［M］.Addison-wesley Reading Menlo Park，1989.

［6］戴晓晖，李敏强，寇纪淞.遗传算法理论研究综述［J］.控制与决策，2000，15（3）：263-268+273.

［7］李敏强，寇纪淞.遗传算法的一种非单调适应值标度变换方法［J］.自然科学进展，2001，11（5）：530-536.

［8］张彤，王宏伟，王子才.变尺度混沌优化方法及其应用［J］.控制与决策，1999，14（3）：285-287.

［9］Back T.Evolutionary algorithms in theory and practice: evolution strategies，evolutionary programming，genetic algorithms［M］.Oxford University Press Oxford，1996.

［10］靳国才，刘夫云，邓聚才.汽车动力总成悬置系统的优化研究［J］.机械科学与技术，2014，33（2）：271-275.

［11］时培成.汽车动力总成悬置系统隔振分析与优化研究［D］.合肥：合肥工业大学，2010.

［12］孙蓓蓓，张启军，孙庆鸿，等.汽车发动机悬置系统解耦方法研究［J］.振动工程学报，1994，7（3）：240-245.

［13］阎红玉，徐石安.发动机—悬置系统的能量法解耦及优化设计［J］.汽车工程，1993，15（6）：321-328.

［14］吴飞，胡朝辉，成艾国，等.综合考虑解耦率和隔振率的发动机悬置系统多目标优化［J］.汽车工程，2013，30（1）：18-22.

Decoupling Optimization of anAutomotive Powertrain Mount System Based on GeneticAlgorithm

WU Jian-wei，LIU Fu-yun，LIQiao，ZHOU Hong-wei，LI Ying-di
（School of Mechanic and Electronic Engineering，Gulin University of Electronic Technology，Guilin 541004，Guangxi China）

To avoid the local optimal solution of the automotive powertrain system by traditional optimization algorithm，the system was optimized by genetic algorithm.The principles of the selection of design variables，the extraction of constraint functions and the selection of the objective functions were deeply analyzed.On this basis，taking the stiffness parameters of the mounting system as the design variables，the scope and the interval of natural frequency as the constraint function，and the decoupling rate of the 6 degrees-of-freedom as the objective function，the powertrain mounting system was optimized by genetic algorithm using MATLAB.The optimization system for powertrain mounting system decoupling of automobiles was developed based on the genetic algorithm.As an example，the powertrain mounting system of a vehicle was optimized.The results show that the distribution of the natural frequency and decoupling rate of the system are greatly improved，and the efficiency and accuracy are greatly raised.

vibration and wave；powertrain；mounting system；genetic algorithm；optimization；MATLAB

U461.1

ADOI编码：10.3969/j.issn.1006-1335.2015.05.016

1006-1355（2015）05-0077-05

2014－12－22

国家自然科学基金项目（51265006）；广西科技开发项目（桂科攻1348005-11）；柳州市科技开发项目（2013H020401）；桂林电子科技大学研究生教育创新计划资助项目（GDYCSZ201442）

伍建伟（1989－），湖南永州人，硕士生。研究方向为机械动力学及优化算法研究。E-mail:wujianwei081x@163.com

刘夫云，教授，博士。

E-mail:liufuyun310@aliyun.com