非线性系统随机振动响应限界极大极小控制

张　巍，应曌中，应祖光

（1.浙江理工大学　经济管理学院　实验中心，杭州310018；2.浙江大学　竺可桢学院，杭州310058；3.浙江大学　航空航天学院力学系，杭州310027）

非线性系统随机振动响应限界极大极小控制

张巍1，应曌中2，应祖光3

（1.浙江理工大学经济管理学院实验中心，杭州310018；2.浙江大学竺可桢学院，杭州310058；3.浙江大学航空航天学院力学系，杭州310027）

研究非线性系统随机振动的限界极大极小最优控制。引入调控变量放大振动峰响应，用高阶多项式作为性能指标函数，提高其中峰值占比，建立非线性随机振动峰响应的极小化最优控制问题方程；应用随机动态规划原理建立HJB方程，考虑控制作用的有界性，确定半连续与跳变型极大极小最优控制律；最后通过数值结果，说明该最优控制能够有效地抑制非线性随机振动，并调控变量、控制界限、跳变型控制等对于控制效果的影响。

振动与波；最优控制；控制饱和；非线性随机振动；峰响应降低

振动响应峰值的降低，例如地震等强激励产生的振动幅值抑制，是工程结构控制的一个重要研究主题，对于提高结构的强度具有重要意义［1-3］。振动最大响应的最小化控制是一个极大极小控制问题［4］。然而，振动响应峰值难以解析地表达，导致最优控制设计的困难，有关研究相对很少。Soong等提出对于响应峰值的近似控制性能指标表达［4］，文［5］发展了响应峰值最优控制的调控策略，并给出理论分析与数值验证。因实际的控制大小是有限的，需要考虑限界或饱和的最优控制问题，关于参外激系统响应的限界最优控制已有一定研究［6-10］。但非线性随机振动的限界极大极小（最大响应最小化）控制策略尚有待于发展。

随机动态规划原理是确定非线性系统随机振动最优控制的一个基本理论，响应峰值的极小化可以设计一定的控制性能指标通过缩放调控实现，控制饱和可作为一个约束结合到极大极小设计，其中限界的最优控制包括半连续与跳变情形。本文选用高阶多项式作为性能指标函数，引入一个调控变量放大其中大响应；然后基于随机动态规划原理建立动态规划（HJB）方程，结合控制限界约束条件，确定半连续与跳变型极大极小最优控制律；最后通过数值结果说明控制效果。

1　非线性系统随机振动响应峰值的最优控制问题方程

考虑下列非线性随机系统

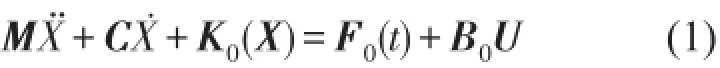
式中X是位移向量，M、C分别是质量与阻尼阵，K0是非线性保守力，F0是高斯白噪声，U是控制力向量，B0是其位置阵，控制的限界约束为UÎ［U1，U2］。对于振动峰值控制，引入一个调控变量xc，变换方程（1）并转化为状态方程［5］

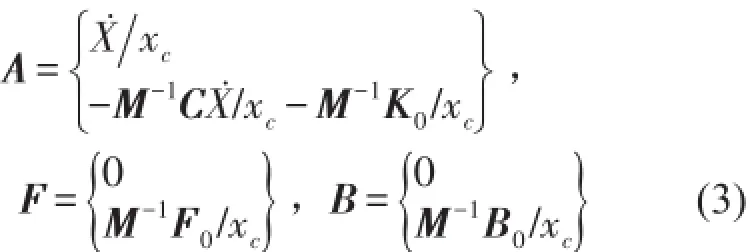
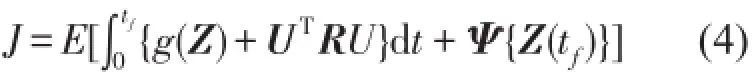
系统（2）随机最优控制的目标是极小化下列性能指标式中E［·］是期望算符，tf是控制的终时，R是对称权参数阵，g（Z）³0，ψ是控制终值。对于半连续限界控制，R正定；对于跳变控制，R取零。响应峰值通过变量xc放大，则g取高阶多项式将提高指标（4）中峰值的占比，从而使J的极小化增强对于峰值的抑制。关于J切近峰值的分析见文［5］。因此，系统（2）和指标（4）组成一个限界的极大极小控制问题。

2　限界的极大极小半连续与跳变控制律

根据随机动态规划原理，建立系统（2）和指标（4）的HJB方程［11］

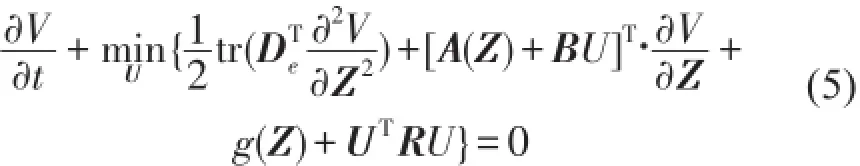
式中V是值函数，De是白噪声强度阵。由式（5）左边第二项泛函极小，并考虑控制U的限界约束条件，可得极大极小控制的最优反馈律。半连续型的限界最优控制律为

式中Ui、U1i、U2i、UVi分别是U、U1、U2、UV的第i个元数，UV=-R-1BT¶V/¶Z/2。跳变型的限界最优控制律为

将式（6）或（7）代入（5）得到关于V的方程，由此确定最优控制U*的跳变条件。适当选择高阶函数g，可得相应的值函数解，式（6）中的函数UV为

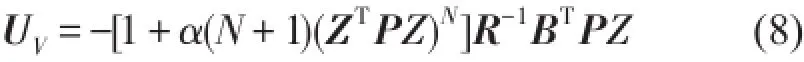
其中α、N是常数，对称常数阵P由下列Riccati方程确定

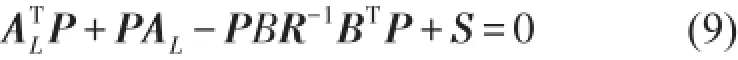
式中AL是A的线性化系数阵，S是g的二次型系数阵。控制（6）与（7）都是有界的，前者保留了界限内的连续性控制律，而后者总是达到其界限，故代价也更高，两者分别是相应极大极小控制问题的最优解。由式（6）或（7）确定最优控制，分别代入（1）可计算系统控制前后的响应，比较控制效果。

3　算例与控制效果

考虑单自由度非线性随机系统

式中x是位移，m、c、k分别是质量、阻尼与线性刚度，k3是非线性刚度，f0是高斯白噪声，u是控制力，限界约束为uÎ［u1，u2］。引入调控变量xc，变换方程（10）为状态方程（2），对于指标（4），建立HJB方程（5），得到极大极小半连续型最优控制（6）与跳变型最优控制（7），分别代入（10）计算系统控制前后的响应。

设系统（10）的参数m=1 kg，c=1 Nsm-1，k=10 Nm-1，k3=10 Nm-3，u1=-5 N，u2=5 N，取xc=0.5 m，R=1 N-2，S=30 diag［1，4］m-2，α=0.3，N=1。分别按式（6）与（7）确定最优控制，用龙格-库塔法计算受控与未控系统的位移，并计算相应的响应标准差，结果如图1—图5所示。图1是随机激励样本，图2展示半连续限界控制前后的位移样本，其响应峰值与标准差分别降低80.4%、82.0%（控制标准差为3.22），可见该限界极大极小控制达到好的非线性随机振动抑制效果。图3表明调控变量的减小（xc=0.1 m）可进一步降低振动位移，此时响应峰值与标准差分别降低85.8%、87.1%。图4表明控制界限的适当扩大（u2=-u1=10 N）可改善振动控制效果，此时响应峰值与标准差分别降低84.4%、85.2%，但改进是有限度的。图5展示跳变限界控制前后的位移样本，其响应峰值与标准差分别降低87.3%、91.8%（控制标准差为5.0），可见在相同条件下跳变型控制效果优于半连续型控制，但控制标准差也更大。因此控制策略需要结合效果与成本综合确定。

图2　半连续控制前后位移（xc=0.5，u2=5）

图3　半连续控制前后位移（xc=0.1，u2=5）

图4　半连续控制前后位移（xc=0.5，u2=10）

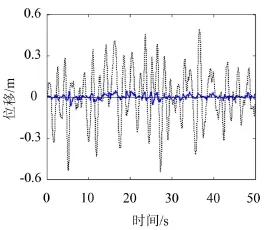
图5　跳变控制前后位移（u2=5）

4　结语

本文提出非线性系统随机振动的限界极大极小最优控制策略。通过引入调控变量，放大振动峰响应，用高阶多项式作为性能指标函数，并考虑控制作用的有界性，建立非线性随机振动峰响应的极小化最优限界控制问题方程。应用随机动态规划原理建立HJB方程，结合控制限界约束条件，对半连续与跳变型限界控制分别得到两类非线性随机振动的极大极小最优控制律。数值结果表明，该最优控制能够有效地抑制非线性随机振动，通过减小调控变量可进一步提高控制效果，增大控制界限可有限度地改善控制效果，跳变型控制比半连续型控制更有效，但总控制作用耗费也更高。

［1］Housner G W，Bergman L A，Caughey T K，et al. Structural control:past，present，and future［J］.ASCE Journal of Engineering Mechanics，1997，123:897-971.

［2］Spencer B F，Nagarajaiah S.State of the art of structural control［J］.ASCE Journal of Structural Engineering，2003，129:845-856.

［3］Soong T T，Cimellaro G P.Future directions in structural control［J］.Structural Control Health Monitoring，2009，16:7-16.

［4］Wu Z，Lin R C，Soong T T.Non-linear feedback control forimprovedpeakresponsereduction［J］.Smart Materials and Structures，1995，4:A140-147.

［5］Ying Z G，Ni Y Q.Optimal control for vibration peak reduction via minimizing large responses［J］.Structural Control Health Monitoring，2015，22:826-846.

［6］Maurer H，Osmolovskii N P.Second order optimality conditions for bang-bang control problems［J］.Control and Cybernetics，2003，32:555-584.

［7］Dimentberg M F，Iourtchenko D V，Bratus A S.Optimal bounded control of steady-state random vibrations［J］，Probabilistic Engineering Mechanics，2000，15:381-386.

［8］Potter J N，Neild S A，Wagg D J.Generalisation and optimization of semi-active，on-off switching controllers for single degree-of-freedom systems［J］，Journal of Sound and Vibration，2010，329:2450-2462.

>

［1］马大猷.噪声与振动控制工程手册［M］.北京：机械工业出版社，2002.

［2］哈里斯（Harris，C.M.），皮索尔（Piersol，A.G.）著；刘树林等译.冲击与振动手册（第5版）［M］.北京：中国石化出版社，2007.

［3］张欣.低压载水型油船的总体振动性能研究［D］.大连：大连理工大学，2013.

［4］王娜.半潜式起重生活平台总体振动特性预测［J］.噪声与振动控制，2013，33（3）：34-37.

［5］林哲，赵德有.大型及超大型油船振动分析方法研究［J］.大连理工大学学报，1997，（4）：88-92.

［6］王显正.船舶总振动特性研究［D］.大连：大连理工大学，2006.

［9］Ying Z G，Ni Y Q，Duan Y F.Parametric optimal bounded feedbackcontrolforsmartparameter-controllable compositestructures［J］.JournalofSoundand Vibration，2015，339:38-55.

［10］张巍，应祖光，胡荣春.拉索非线性随机振动的最优有界半连续控制［J］.噪声与振动控制，2014，34（2）：133-135.

［11］Stengel R F.Optimal Control and Estimation［M］.New York:John Wiley&Sons，1994.

Optimal Bounded Control of Large Random Vibration Responses in Nonlinear Systems

ZHANGWei1，YING Zhao-zhong2，YING Zu-guang3
（1.Laboratory Center，School of Economics and Management，Zhejiang Sci-Tech University，Hangzhou 310018，China；2.Chu Kochen Honors College，Zhejiang University，Hangzhou 310058，China；3.Department of Mechanics，School ofAeronautics andAstronautics，Zhejiang University，Hangzhou 310027，China）

The optimal bounded minimum-maximum control for random vibration of nonlinear systems was studied.A variable was employed for rescaling system responses and a high-order power polynomial was used as the cost function of performance index for magnifying large vibration responses.The optimal bounded minimum-maximum control problem for nonlinear random vibration was expressed by a transformed differential equation and a performance index of the system. Then，the HJB equation was derived based on the random dynamical programming principle.The optimal bounded semicontinuous and switching control laws were obtained by solving the equation with the consideration of the control bound. The control effects for different variable values，control bounds，semi-continuous control and switching control were compared one-another.Numerical results show that the proposed control can effectively suppress the nonlinear random vibration.

vibration and wave；optimal control；control saturation；nonlinear random vibration；peak response reduction

O32；TB53

ADOI编码：10.3969/j.issn.1006-1335.2015.05.010

1006-1355（2015）05-0053-03+59

2015－02－28

国家自然科学基金项目（11432012）；浙江省自然科学基金项目（LY15A020001）

张巍（1965－），女，江苏南通人，高级工程师，学士，主要从事信息系统与控制研究。

E-mail:zhweihz@zstu.edu.cn