反导预警作战资源调度方法

赵新爽，汪厚祥，蔡益朝

（1．空军预警学院空天预警实验室，湖北武汉430019；2．海军工程大学电子工程学院，湖北武汉430033）

反导预警作战资源调度方法

赵新爽1，2，汪厚祥2，蔡益朝1

（1．空军预警学院空天预警实验室，湖北武汉430019；2．海军工程大学电子工程学院，湖北武汉430033）

针对反导预警作战中多部预警资源协同探测多批弹道导弹目标的问题，根据反导预警作战资源调度的特点，提出了反导预警作战任务分解策略，并以调度效益、交接次数和资源负载均衡度为目标建立了多目标优化模型。通过重新设计粒子编码方式以及对重新定义粒子群优化算法中的位置更新公式，使其适用于求解离散变量优化问题。针对粒子群优化算法容易过早收敛的缺点，在进行局部搜索时使用变邻域搜索算法，从而增强算法的寻优能力。通过仿真实验验证，将两种算法相结合能够快速有效地解决反导预警作战资源调度问题。

资源调度；粒子群－变邻域搜索；多目标优化问题；反导预警

0 引 言

反导预警作战资源调度面向的是对处于中段飞行的中远程弹道导弹进行预警探测时，预警任务对资源的分配问题。由于中远程弹道导弹飞行距离远，没有一部地基雷达能够单独地完成整个飞行阶段的预警探测任务，需要多部雷达对同一目标进行接力跟踪。而如果同时出现多批目标，在目标与预警资源的可见关系改变、雷达跟踪目标容量限制以及目标威胁程度变化等因素的作用下，如何有效地调度可用的预警资源，使其能最好地完成预警探测任务是一项必须解决而又棘手的问题。

目前，对反导预警作战资源调度方面的研究大部分集中在天基预警系统的资源调度上，文献［1－4］对天基预警系统中的低轨卫星资源调度问题进行了研究，建立了该问题的约束满足问题模型，并设计了一些算法求解相应的模型。而在利用地基预警装备进行弹道导弹预警探测的资源调度方面，目前极少有人研究。地基预警探测的资源调度与天基预警探测的资源调度有着很大的不同：首先，天基预警资源只有低轨卫星一种，而地基预警资源有P波段远程预警雷达和X波段多功能地基雷达，在进行预警探测时，这两种雷达有不同的优先级；其次，利用天基预警资源探测目标时，需要多部资源同时探测一个目标，而一部地基预警装备可以同时探测多批目标。而且，文献［1］所建立的模型都是单目标的优化模型，不能够很好地反映反导预警作战资源调度的问题。

针对此，本文建立了反导预警作战资源调度的多目标优化模型，并设计一种粒子群－变邻域搜索算法求解调度模型，进而利用仿真实验验证该算法的性能。

1 反导预警任务分解

在预警探测任务的执行过程中，预警任务必须指派到预警装备上才可以直接执行，而目标与预警资源之间复杂的可见关系给预警任务的指派带来了极大难度。任务分解是处理这种复杂关系很好的手段。任务分解是指将复杂的任务细化为能由作战资源直接执行和完成的元任务序列。这里的元任务是指不再进行分解、可直接一次性执行的最基本任务［5］。经过任务分解后，每个元任务都会对应一个可用的预警资源集合。预警任务分解极大地降低了任务与资源之间复杂的对应可见关系，同时，将调度周期内的预警任务分解为一系列的元任务，每个元任务都对应一个或多个可用资源，只需从中选择一个执行该元任务即可。而对整个预警探测任务而言，在每个元任务对应的可用资源集中挑出一个资源即可形成一个满足预警探测任务需求的调度方案。

1．1 任务分解策略分析

不同的任务分解策略往往会得出不同的元任务集，最终导致调度方案也不同。目前，比较常见的任务分解策略有两种，分别是“基于最长观测时间”和“基于均匀分割”。“基于最长观测时间”的任务分解策略的思想是在任意一个必须对目标进行交接的时间点处，在其可选的资源中，寻找一个对目标观测时间最长的资源作为切换的对象。该分解策略的优点是能减少目标在预警资源之间的频繁交接，而缺点是可能出现某些元任务的执行时间过短的情况。预警资源在对目标进行探测时，需要一定的时间才能进入稳定跟踪状态，元任务对应的时间区间过短可能导致预警资源还没有对目标形成稳定航迹就必须放弃探测任务，从而导致该目标丢失。“基于均匀分割”的任务分解策略的思想是设定一个最小的区间长度Tm，每隔Tm时间对预警任务划分一次，每个元任务对应的区间长度为Tm的整数倍。该分解策略优点是分解方式简单，任务执行的时间比较固定。但是在分解时，元任务对应的最小区间长度很难确定，太短则会引起频繁的切换，太长则可能导致没有一个预警资源能独立地执行该元任务。

另外，文献［3］设计了一种基于关键点的预警任务分解策略，但该策略针对的是天基预警系统资源调度过程，而且该分解过程复杂，可操作性不强，不适合本文预警资源调度的特点。以上3种任务分解策略都不适用于对反导预警作战任务的分解。

1．2 反导预警作战的任务分解策略

根据反导预警过程和反导预警资源的特点，结合后续资源调度建模的需要，在对预警任务进行分解时，要遵守以下约束条件：

（1）两个相邻的元任务在时间上不要求是必须紧密衔接的，但是其间隔不能超过特定阈值T0，以保证在该时间间隔内目标不会丢失。

（2）每个元任务对应时间区间内的预警资源不发生变化，即在对预警资源进行调度时，可以从每个元任务的可用资源集中任选一个来完成对该元任务的全程探测。

（3）每个元任务具有最短持续时间Tmin，以保证预警资源能进入稳定跟踪状态。

在以上约束的限制下，本文设计出反导预警作战的任务分解策略，其步骤如下：

步骤1 计算所有预警资源同目标的可见时间窗口。

步骤2 按可见时间窗口的端点进行分割。找出每个可见时间窗口的端点，根据这些端点将整个预警任务涵盖的时间区间进行分割，由于每一个时间片是通过窗口的端点进行划分的，因此可以保证每个时间片对应的可用预警资源不发生变化。

步骤3 检查每两个相邻端点之间的区间。如果该区间内没有预警资源可用，而且该区间长度超过了T0，则无论采用何种任务分解策略，都会存在预警的盲区，只有增加或者重新部署预警资源，否则预警任务会失败；如果不存在这样的区间，则开始预警资源的优化调度。

预警任务经过分解后，可以得到一系列的元任务，此时，预警资源的调度问题就转化为对这些元任务调度的问题，即确定哪些元任务要执行，如果执行，应该分配哪个预警资源进行执行。

2 调度模型

调度周期内的每一个目标对应一个预警探测任务，按照反导预警作战的任务分解策略进行任务分解后，每个预警探测任务可以分解为多个元任务，而每个元任务都对应着若干个可用的资源，因此，对该调度问题存在着很多种可行的调度方案。对预警资源进行调度并不是要找到一个可行的调度序列，而是找到能使整个系统调度的目标完成得最好的调度序列。

2．1 符号说明

为准确描述反导预警作战资源调度问题，先定义以下一些符号：MS表示当前所有预警探测任务的集合；NMS表示当前预警探测任务的数量，即当前目标的数量；Rsc表示当前可用预警资源的集合；NRsc表示当前可用预警资源的数量；STsk（i）表示第i个预警探测任务经过分解后得到的所有元任务的集合；Rsci［j］表示第i个任务的第j个元任务的可用预警资源集合；Ti表示第i个任务的持续时间；STimei［j］、ETimei［j］和Ti［j］分别表示第i个任务的第j个元任务的开始时间、结束时间和持续时间；Pri［j］和Erri［j］分别表示第i个任务的第j个元任务的优先权和探测精度；Err表示拦截武器系统要求预警系统提供的目标指示精度；Benr表示预警资源r的优先权；Nr表示资源r的最大跟踪数量；WTr表示资源r的总计工作时长；EWT表示当前所有资源的平均工作时长。

2．2 决策变量

2．3 目标函数

反导预警作战资源调度的目标可以从以下3个方面进行刻画：

（1）从整个反导预警系统的角度来看，要尽可能提高调度产生的效益，即尽量多地完成优先权高的元任务，而且尽量用优先权高的预警资源完成。元任务的优先权与目标的探测精度和目标距离落地时间有关，将其定义为

式中，ω1，ω2为目标探测精度和距离落地时间对应的权重，其中ω1＋ω2＝1。定义预警资源的优先权为

于是

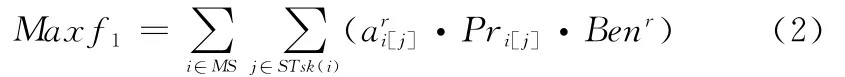
（2）从对每一个任务执行的角度来看，要尽量减少目标在不同预警资源间交接的次数，即

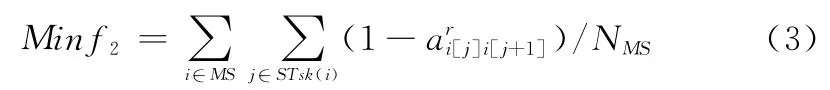
（3）从资源利用的角度来看，期望每个预警资源能得到最大限度的利用，同时又要尽量让预警资源负载均衡，即

式中

2．4 约束条件

（1）预警资源的最大跟踪目标数量限制

（2）每个元任务只能在其备选资源集上选择资源执行

（

3）每个元任务只占用一个资源只被执行一次

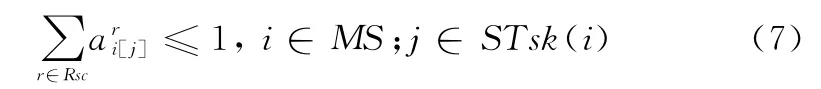
（4）当时间跨度超过T0的元任务不能被成功执行时，其后续的元任务也不能执行

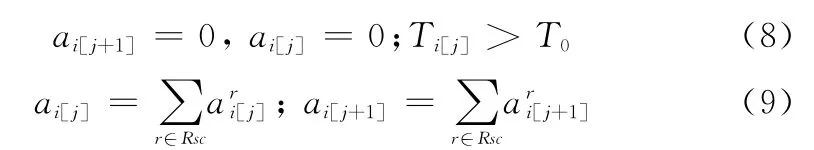
（5）当某个元任务的持续时间小于要求的最短持续时间时，要求它与其紧前或者紧后的元任务使用同一预警资源进行探测

3 基于粒子群－变邻域搜索求解反导预警作战资源调度模型

反导预警作战资源调度问题可以归结为一个多目标优化模型，目前对于多目标优化模型的求解方法较多，其中，粒子群优化（particle swarm optimization，PSO）算法在解决该类问题上具有较大优势［6］。PSO算法中多个粒子同时进行搜索，这种并行的搜索方式有助于快速地找到多目标优化问题非支配解［7］，同时，PSO算法具有较强的通用性，对目标函数和约束条件没有过高的要求，而且容易与其他算法相结合，从而对自身的缺陷进行改进，快速有效地得到最优解。但是，标准的PSO算法针对的是连续的实数型粒子编码，而本文中模型的决策变量为整数变量，不能直接使用标准PSO算法中的公式对粒子位置和速度进行更新。同时，与其他智能搜索算法一样，PSO算法有早熟和易陷入局部最优解的缺陷［8］。本文首先重新定义粒子的位置更新公式，然后将PSO算法与变邻域搜索（variable neighborhood search，VNS）结合起来求解所建立的模型。

3．1 粒子编码方式

本文建立的资源调度模型是一个多目标整数规划模型，如果按照离散粒子群算法常用的二进制编码方式进行编码［9］，需要判断每个元任务与每一个可用资源之间的指派关系，从而导致粒子的维度巨大，严重影响算法的运行效率，对此，重新设计编码方式如下：

3．2 粒子位置更新策略

上述编码方法简单、直接，但由于粒子在各个维度上的取值均为整数，所以不能直接使用标准粒子群算法中的公式对位置进行更新［10］，本文对连续粒子群算法的公式进行修改，定义位置更新公式如下：

式中，ω、c1、c2以及和gBk的定义与标准粒子群算法中相同；f1，f2和f3是操作算子。粒子位置更新公式（11）由3部分［11］组成。

（1）粒子根据自身当前的状态进行调整的部分

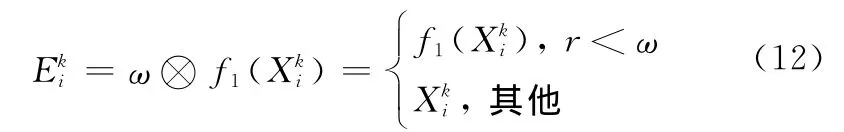
该式的具体实现方法为：首先产生一个（0，1）之间的随机数r，如果r＜ω，则定义ω⊗f1（）＝f1（），否则为。f1（）的实现方法为：针对粒子编码，随机产生一个1～L之间的整数a，其中L为粒子编码长度，在Xki中a位置对应的可选预警资源中随机选择一个，替换原来的预警资源。

（2）粒子根据自身最优位置pBki进行调整的部分

该式的具体实现方法为：首先产生两个（0，1）之间的随机数r1和r2，如果r1＜c1，则执行，其中采用POX（precedence preserving order based crossover）算子进行操作［11］，首先随机地将任务集划分为两个子集Q1和Q2，这两个子集都非空；接着挑选出中与Q1有关的分量，将其复制到子代1，复制中针对任务Q1的分量到子代2，并都保持分量原来的位置顺序不变；复制中针对Q2的分量到子代1，复制中针对Q2的分量到子代2，并都按照原来的位置顺序进行排列；最后选择其中一个作为后代。如果r2＜c1，则执行＝g（，），其中g（，）采用MPX（rand－point preservation crossover）算子进行操作［12］，首先产生一个与粒子维数相等数组RA，RA中所有元素的值都为（0，1）区间内的随机数；接下来遍历数组RA，若RA中的数小于p（p∈（0，1）），则记录下相应的位置，复制中同样位置上的预警资源号到，这里，其中iter和gen分别为迭代次数和当前运行代数；利用MPX算子对g（，）进行操作，其中p的值可以自适应调整，从而对提高获得最优解的概率有一定的帮助。

（3）粒子根据全局最优位置gBk进行更新的部分

其中，对f3（，g）的操作与g（，p）相同。

3．3 多目标全局搜索策略

为了避免粒子在全局搜索过程中快速趋同，引入粒子适应度的概念。精英集中第i个粒子的适应度的定义如下：

其中，E为精英集，而

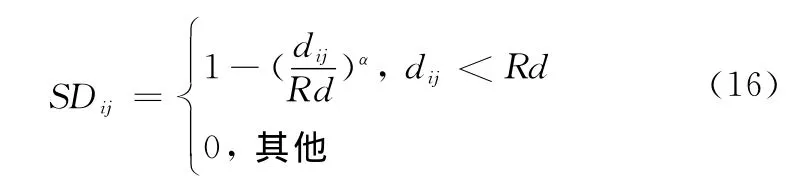
式中，dij表示两个粒子之间的空间距离；Rd为一个固定的值；α为调节参数。通过定义粒子的适应度，并将其作为依据，可以对精英集中的粒子进行筛选，从而使整个粒子群具有良好的学习信息。

3．4 多目标局部搜索策略

采用式（11）的方式更新粒子位置时，粒子直接在离散域中进行更新，收敛速度快，但是粒子的搜索容易出现停滞。对此，本文结合PSO算法与VNS算法，对局部搜索的过程进行改进。

VNS算法由Hansen［13］首次提出，其基本思想是：基于一定的初始解，设计若干种邻域结构，这些邻域结构产生的邻域解对现有局部最优解的扰动不断扩大［14］，首先在第一个邻域结构内搜索局部最优解，当这个最优解无法得到有效更新时，改变邻域结构继续搜索，直至获得理想的最优解或者达到最大迭代次数［15］。

对于本文所建立的反导预警资源调度模型，结合PSO算法，对每个局部最优解执行变邻域搜索的过程为：

步骤1 初始解构造。设定VNS算法以PSO算法最后一代群体中的部分优秀个体极值作为初始解。

步骤2 产生邻域解。根据反导预警作战资源调度的特点设计3种邻域，分别为：邻域1是在局部最优解对应的调度方案中任选两个元任务，交换他们所对应的预警资源；邻域2是在局部最优解对应的调度方案中任选两个元任务，交换与之相邻的两个元任务（左或右）的对应的预警资源；邻域3是在局部最优解对应的调度方案中任选两个元任务，交换与之相邻的左右两个元任务的对应的预警资源。这3个邻域结构对现有调度方案的扰动程度不断变大，对于这3种邻域的每次交换，首先要判断交换之后是否能满足模型中的约束条件，如果能则执行交换；如果不能，则再次任选两个元任务，以此为基准再次进行交换并判断交换后能否满足模型中的约束条件。

步骤3 局部搜索。按照邻域1到邻域3的顺序依次选择一种邻域结构，在该邻域结构内采用穷举的策略，搜索整个邻域内的可行解，运用目标函数评价局部搜索的效果，从而选取最优解。

步骤4 当前最优解更新。比较原有最优解与当前获得的最优解，保留较好的一个作为当前最优解，并决定是否更换邻域结构继续进行搜索。

步骤5 当任意邻域都不能使当前解得到进一步的优化时，重新选择一个初始解，开展新的搜索过程［16］，当算法迭代的次数达到最大迭代次数MaxIter时，算法退出，输出当前最优解。

将PSO与VNS结合起来求解预警探测任务周期重调度模型时，首先基于PSO算法得到模型的一个或多个较优解，并将这个（些）解作为VNS算法的初始解，再进行局部搜索得到最优解。整个算法的具体流程如下：

步骤1 确定参数。设定粒子群中粒子的个数P，循环的代数G，进化的周期数gen，PSO公式中的常量ω、c1和c2，VNS中的最大迭代次数MaxIter。

步骤2 种群初始化。初始化粒子群的位置为X1，X2，…，Xp。

步骤3 根据Pareto支配关系，将非支配解置入精英集中，并随机选择一个非支配解作为全局最优值gB，同时，初始化局部最优值pBi＝Xi（i＝1，2，…，P）。

步骤4 根据式（11）更新粒子位置。计算新种群中粒子的适应度值，并更新精英集、pBi和gB。若精英集已满，则剔除其中适应度最小的一个粒子，并从精英集外选择适应度最大的粒子加入精英集。

步骤5 从所有的局部最优解中选择N个较优的个体作为初始解，对每个解分别执行VNS，同时更新粒子位置、局部最优位置和全局最优位置，输出最优解。

步骤6 若精英集连续gen代没有改进，则从精英集中随机地挑选出若干个粒子替代种群中相同数量的粒子。

步骤7 若迭代的次数达到MaxIter，则输出最优值；否则，转入步骤3。

这种将PSO的快速搜索能力和VNS的局部探索能力相结合的混合算法称为粒子群－变邻域搜索（PSO－VNS）算法。

4 仿真实例

以具体的仿真运行为例，设置两组不同的仿真场景，分别利用PSO－VNS算法、非支配排序遗传算法（nondominatedsorting genetic algorithm，NSGA）以及多目标粒子群优化算法［17］（muti－objective PSO，MOPSO）对模型进行求解，通过比较求解的结果和运行的时间来对不同算法的性能进行分析。两组不同的仿真场景分别设定10枚（FBM＿1～FBM＿10）和20枚（FBM＿1～FBM＿20）同一型号的中远程弹道导弹目标，从不同位置发射，同时攻击某一地区。表1给出了10枚导弹的弹道参数（包括发落点的经度和纬度、射程以及导弹飞行时间）。

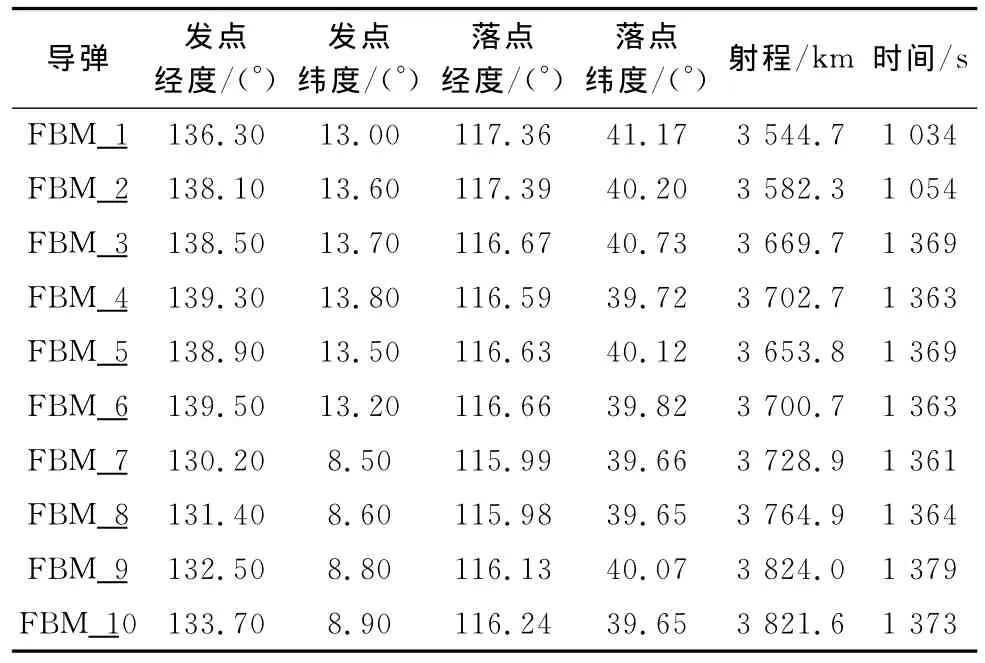
表1 导弹弹道参数配置表

反导预警系统包含6部单阵面P波段远程预警雷达（P1～P6），分别部署在山东、湖南、安徽、江西、河北以及黑龙江，4部X波段多功能地基雷达（X1～X4），部署于P波段雷达周边。表2给出了这10部预警资源对第一枚导弹的可见时间窗口。

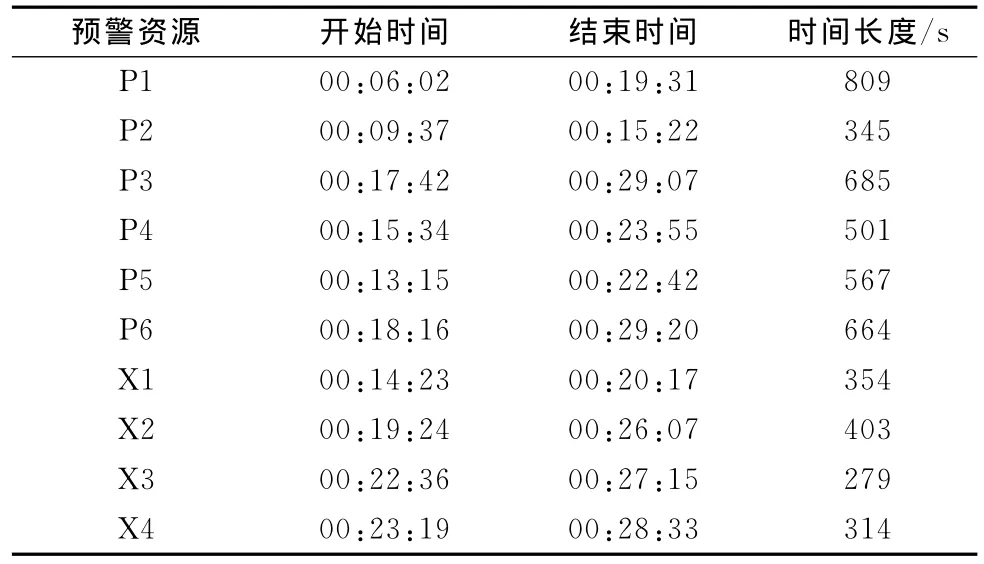
表2 目标1的可见时间窗口

多目标优化模型中目标探测精度和距离落地时间对应的权重取值ω1＝ω2＝0．5，拦截武器系统要求的目标指示精度设定为Err＝300m。PSO－VNS中参数设置如下：设定种群的规模P＝20，最大循环代数G＝200，惯性常量ω＝0．9，学习因子c1＝c2＝2，精英集中解的个数N＝10，进化停滞周期gen＝10，最大迭代次数MaxIter＝5。

在Pentium IV 2．8－GHz，内存2GB的计算机上对每组场景进行10次独立实验，3种算法所获得非支配解的数量、调度效益、任务平均交接次数、资源负载情况以及运行时间如表3所示。非支配解的数量和运行时间的计算方法为取10次实验结果的平均值；而调度效益、任务平均交接次数和资源负载的计算方法为先对每次得到的非支配解取平均，然后取10次实验的平均值。从实验结果可以看出，采用3种算法都能得到有效的调度方案，而利用本文提出的算法得到的结果在前4个指标方面都明显好于其他两种算法。而且，随着目标数量的增加，3种算法的运行时间都有所增加，得到的非支配解的数量有所减少，这与实际情况是吻合的。另外，与MOPSO算法的对比还可以说明变邻域搜索确实增强了算法的局部搜索性能，只是在运行时间上有所增加，但处于可以接受的范围以内。

表3 不同场景下3种算法性能比较

5 结 论

本文对反导预警作战资源调度问题进行一些探索性的研究，提出了适合反导预警任务分解的策略，并在此基础上，建立了该问题的模型，提出利用PSO－VNS算法求解该模型。仿真结果表明，PSO－VNS算法能够快速地找到最优调度方案，有效解决反导预警作战资源调度问题。不足的地方在于：所建立的资源调度模型还不够完善，比如目标在资源之间交接的约束条件没有得到反映；同时，对两种预警资源优先权的赋值均为常量，没有考虑相关因素的影响。下一步重点解决以下3个方面的问题：①进一步分析目标交接的方式与条件，并在模型中加以反映；②分析影响预警资源优先权的因素，并建立模型；③构建更多的仿真场景，验证在不同场景下算法的性能。

［1］Du Z S，Yi X Q．Research on satellite scheduling of the spacebased early warning system［J］．Fire Control ＆Command Control，2009，34（7）：32－36．（杜占帅，易先清．天基预警系统资源调度方法［J］．火力与指挥控制，2009，34（7）：32－36．）

［2］Feng M Y，Tang S X，He J．Resource scheduling for spacebased early warning system based on improved particle swarm optimization［J］．Journal of China Academy of Electronics and Information Technology，2010，5（1）：97－101．（冯明月，汤绍勋，何俊．基于改进粒子群算法的天基预警系统资源调度方法［J］．中国电子科学研究院学报，2010，5（1）：97－101．）

［3］Feng M Y，Li G H，Yi X Q．Sensor scheduling method for space－based early warning system［J］．Computer Engineering and Applications，2009，45（2）：225－228．（冯明月，李国辉，易先清．天基预警系统传感器调度方法［J］．计算机工程与应用，2009，45（2）：225－228．）

［4］Tang S X，Yi X Q，Luo X S．An improved particle swarm optimization algorithm for early warning satellites scheduling problems［J］．Systems Engineering，2012，30（1）：116－121．（汤绍勋，易先清，罗雪山．面向预警卫星调度问题的改进粒子群算法［J］．系统工程，2012，30（1）：116－121．）

［5］Dong T，Liu F X，Li X．Task decomposition of terminal phrase multilayer antimissile operation［J］．Modern Defense Technology，2012，40（4）：17－20．（董涛，刘付显，李响．末段多层反导作战的任务分解［J］．现代防御技术，2012，40（4）：17－20．）

［6］Sharaf A M，El－Gammal A A A．Particle swarm optimization PSO：a new search tool in power system and electro technology［M］∥Panigrahi B K，Abraham A，Das S，ed．Computation Intelligence in Power Engineering．Berlin：Springer Verlag，2010：235－294．

［7］Lei D M．A pareto archive particle swarm optimization for multiobjective job shop scheduling［J］．The International Journal of Advanced Manufacturing Technology，2008，37（1／2）：157－165．

［8］Leong Y，Wen F，Gary G．PSO－based multi－objective optimiza－tion with dynamic population size and adaptive local archives［J］．IEEE Trans．on Systems，Man，and Cybernetics—Part B：Cybernetics，2008，38（5）：1270－1293．

［9］Cabrera J C F，Coello C A C．Handling constraints in particle swarm optimization using a small population size［C］∥Proc．of the 6th Mexican International Conference on Artificial Intelligence，2007：41－51．

［10］Alvarez－Benitez J E，Everson R M，Fieldsend J E．A MOPSO algorithm based exclusively on pareto dominance concepts［J］．Lecture Notes in Computer Science，2005，3410：459－473．

［11］Zhang J，Wang W L，Xu X L．Hybrid particle－swarm optimization for multi objective flexible job－shop scheduling problem［J］．Control Theory ＆Applications，2012，29（6）：715－722．（张静，王万良，徐新黎．混合粒子群算法求解多目标柔性作业车间调调度度问题［J］．控制理论与应用，2012，29（6）：715－722．）

［12］Tavakkoli－Moghaddam R，Azarkish M，Sadeghnejad－Barkousaraie A．A new hybrid multi－objective Pareto archive PSO algorithm for a bi－objective job shop scheduling problem［J］．Expert Systems with Applications，2011，38（9）：10812－10821．

［13］Hansen P，Mladenovic N．Variable neighborhood search：principles and applications［J］．European Journal of Operational Research，2001，130（3）：346－354．

［14］Burke E K，Li J P，Qu R．A hybrid model of integer programming and variable neighborhood search for highly－constrained nurse roistering problems［J］．European Journal of Operational Research，2010，203（2）：484－492．

［15］Chen T S，Tang K，Chen U，et al．Analysis of computational time of simple estimation of distribution algorithms［J］．IEEE Trans．on Evolutionary Computation，2010，14（1）：1－22．

［16］Polacek M，Doerner K，Hartl R．A variable neighborhood search for the capacitated arc routing problem with intermediate facilities［J］．Journal of Heuristics，2008，14（5）：405－423．

［17］Tripathi P，Bandyopad S．Multi－objective particle swarm optimization with time variant inertia and acceleration coefficients［J］．Information Sciences，2007，177（22）：5033－5049．

E－mail：xinsher＠163．com

汪厚祥（1960－），男，教授，博士，主要研究方向为网络应用技术和分布式系统。

E－mail：hxwang＠163．com

蔡益朝（1976－），男，副教授，博士，主要研究方向为信息管理与决策支持。

E－mail：cyc＠163．com

Resource scheduling method in antimissile early warning campaign

ZHAO Xin－shuang1，2，WANG Hou－xiang1，CAI Yi－chao2
（1．Space and Air Early Warning Lab，Air Force Early Warning Academy，Wuhan 430019，China；2．Electronic Engineering College，Naval University of Engineering，Wuhan 430033，China）

In order to solve the problem that several equipment detect multi－target in antimissile early warning campaign，the task decomposition strategy based on the endpoint is proposed，which is according to the characteristics of resource scheduling for antimissile early warning．A multi－objective optimization model is established based on this task decomposition strategy，and the objective of this model includes scheduling benefit，handover times and resource loading degree．By redesigning the particle encoding mode and redefinition the position updating formula in particle swarm optimization，the algorithm is suitable for solving the discrete optimization problem．Aiming at the problem of premature，a modified algorithm combining the particle swarm optimization－variable neighborhood search is presented．The experimental results show that this algorithm can resolve the problem of resource scheduling for antimissile early warning rapidly and effectively，and it has good application value．

resource scheduling；particle swarm optimization－variable neighborhood search；multi－objective optimization problem；antimissile early warning

E 844；N 945

A

10．3969／j．issn．1001－506X．2015．06．12

赵新爽（1980－），男，讲师，博士，主要研究方向为指挥控制与优化决策、系统建模与仿真。

1001－506X（2015）06－1300－06

2014－01－03；

2014－10－06；网络优先出版日期：2014－12－09。

网络优先出版地址：http：／／www．cnki．net／kcms／detail／11．2422．TN．20141209．0122．007．html

国家自然科学基金（61302193）资助课题