基于SINGER模型的实时误差配准算法及分析

李 洋，张 靖

（中国电子科学研究院，北京100041）

基于SINGER模型的实时误差配准算法及分析

李 洋，张 靖

（中国电子科学研究院，北京100041）

系统误差配准是多平台、多传感器目标跟踪的关键环节，可以有效地估计雷达跟踪系统误差，并进行准确误差补偿。若不进行精确的系统误差配准，则可能导致多平台、多传感器跟踪系统对目标融合跟踪的错误或对同一目标产生多条航迹，从而导致系统性能恶化。给出了基于目标SINGER运动模型的扩维卡尔曼滤波算法。通过仿真实验分析了误差配准精度与机动频率的关系，结论为针对不同机动频率目标进行雷达跟踪系统的误差配准提供理论参考。

误差配准；SINGER运动模型；扩维卡尔曼滤波；航迹关联

0 引 言

近年来，多平台、多传感器目标跟踪系统由于其高跟踪精度、大跟踪范围和高目标发现概率而受到相关研究人员的重视。但跟踪系统误差在跟踪起始阶段、滤波阶段和航迹关联阶段等始终存在，严重影响跟踪精度和融合结果，甚至导致出现丢失目标、产生虚假目标等问题，降低跟踪系统对目标的监视性能。所以系统误差配准对于形成准确的目标航迹具有重要意义，是建立清晰、一致的战场态势的重要环节［1－2］。

随着跟踪技术的深入发展，各种配准算法相继被提出，目前主要的配准算法包括极大似然配准算法、最小二乘配准算法、实时质量控制误差配准算法、扩维卡尔曼滤波算法等。而扩维卡尔曼滤波算法由于其思路清晰、运算量低等特点而在工程领域大量使用［3－5］。

通常在作战过程中，跟踪目标具有机动特性。SINGER运动模型对于机动目标跟踪具有非常好的效果，其目标的机动特性由机动频率所表征。SINGER运动模型的状态转移表达形式也具有自身独有的特征。本文针对目标SINGER运动模型给出了其扩维卡尔曼滤波算法，并对系统误差进行补偿。分析了机动频率对于补偿精度的影响，为机动目标跟踪系统的误差配准提供理论支撑。

1 状态与量测方程

1．1 SINGER运动模型

SINGER模型是针对加速度期望为零而建立的一阶时间相关模型，其模型［6］具有如下表达形式：

式中，α是机动时间常数的倒数，通常被称为机动频率。机动频率的确切值要经过实际实时测量才能得到，一般情况下对于转弯机动时机动频率通常取1／60，逃避情况下机动频率取1／20，大气扰动取1。

对于方程式（1）进行离散化处理，采样间隔设为T，SINGER模型离散化后状态转移矩阵［7］如下所示

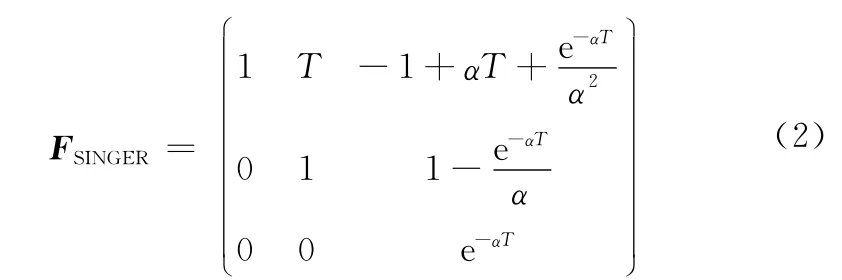
状态转移方程式（1）离散化后的过程噪声协方差矩阵［］为

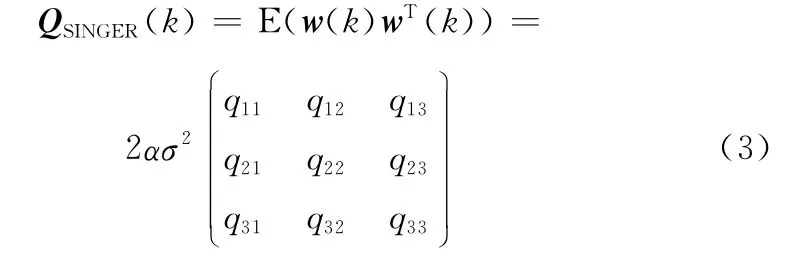
式中

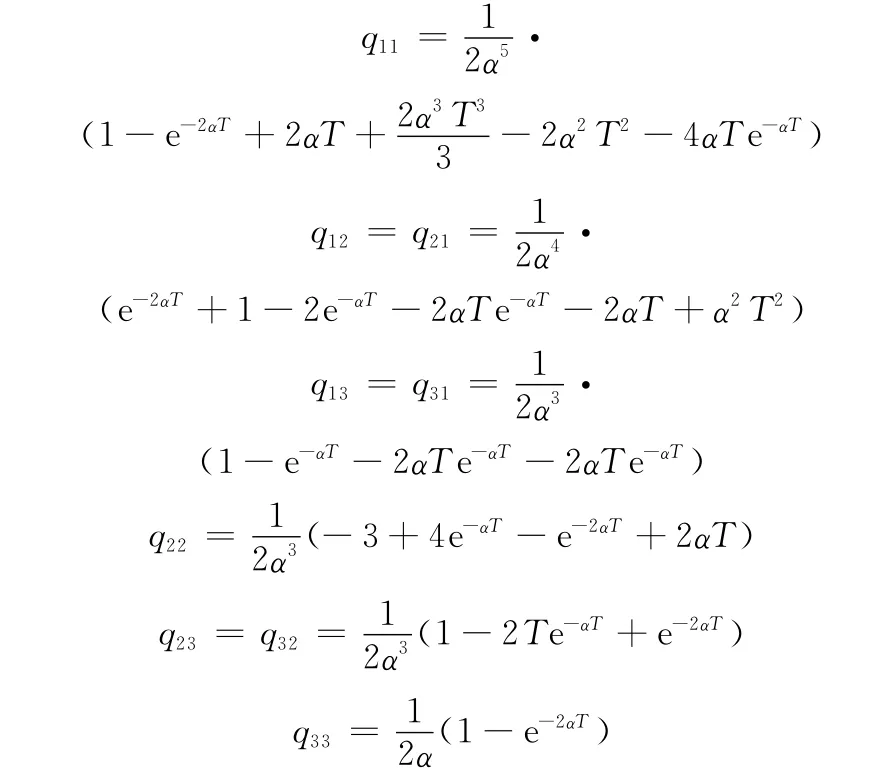
1．2 量测方程与系统误差设置

假设多平台跟踪系统包含两部雷达，同时对一个目标进行跟踪。雷达在极坐标系下进行观测，量测数据存在距离向误差和方位向误差，并满足加性噪声的性质。这样在距离向和方位向系统误差表示为

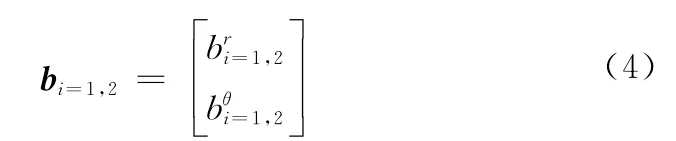
式中，i＝1，2表示多平台跟踪系统传感器标号，上标分别表示距离向和方位向。

传感器i的量测方程表示为

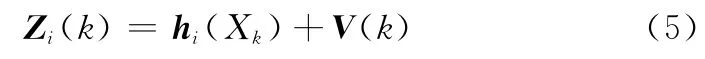
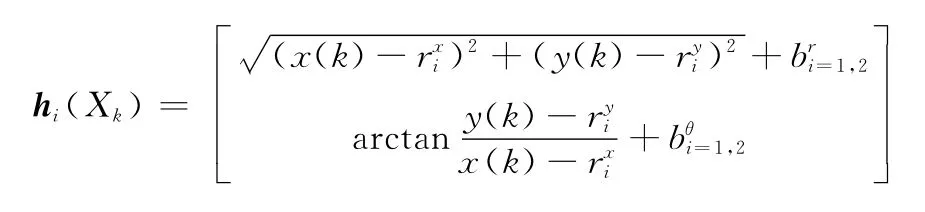
而将极坐标下量测转换为笛卡尔坐标系下量测须将系统误差和量测噪声方差分别进行转换，转换方程［9］如下：

（1）系统误差转换

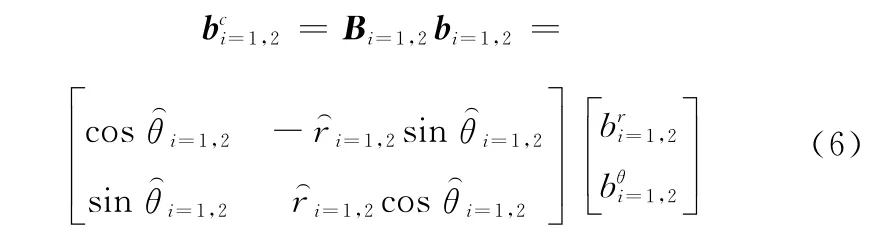
（2）量测噪声方程转换

式中

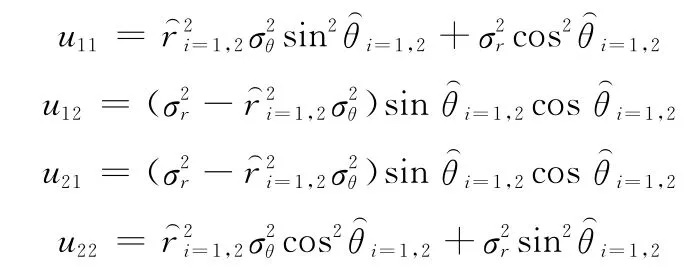
其中，σr和σθ分别表示为极坐标系下噪声V（k）的方差，且满足距离向和方位向噪声量测相互独立。

2 SINGER运动模型目标扩维卡尔曼误差配准

扩维卡尔曼滤波算法的主要思想是将状态空间扩展到状态空间和系统误差空间二者并集上，其维度也相应地得到扩展。考虑系统误差，目标在SINGER运动模型的假设下状态向量更新为

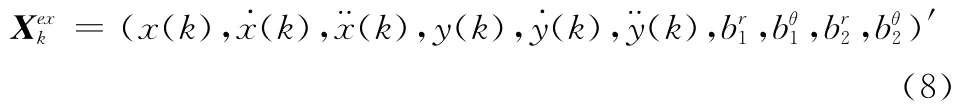
相对于单纯考虑状态空间，式（8）增加了4个维度，分别为传感器1的距离向和方位向误差，传感器2距离向和方位向误差。

目标转移方程为

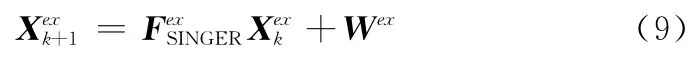
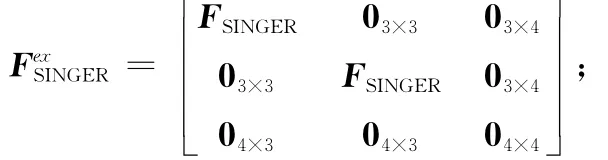
Wex是扩维后的噪声方程矩阵，其方差为

目标量测方程表示为

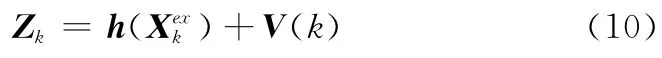
其中

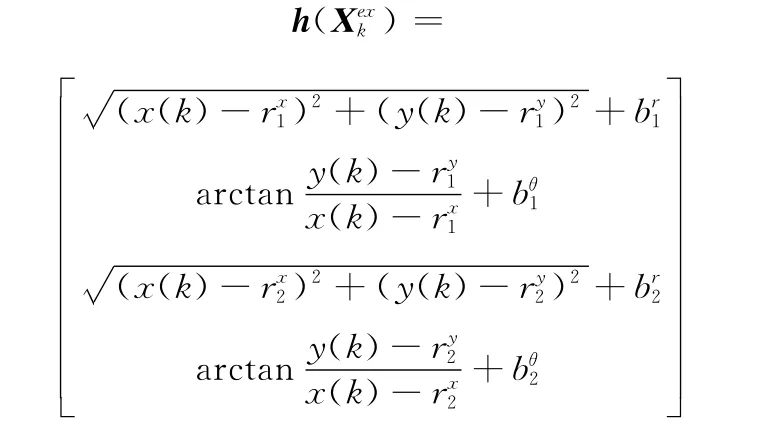
基于SINGER模型的扩维卡尔曼滤波算法步骤如下：

论证会议后的报告修改工作不重视，一些论证企业,在论证会议结束后认为专家组基本同意报告书内容后,不重视修改工作，反复修改，延长论证周期，降低工作效率又影响论证报告书质量。

步骤（3）～步骤（5）中的扩维量测矩阵可以表示为

式中

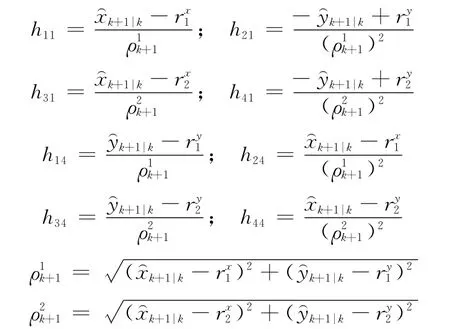
将式（2）～式（11）代入到步骤1～步骤6中就得到了基于SINGER模型多平台目标跟踪系统误差配准算法。

3 仿真验证

在式（9）中，状态转移方程是由目标运动的机动频率决定的，不同的机动频率对应不同的状态转移矩阵和状态转移噪声方差矩阵。所以有必要讨论机动频率与误差配准精度之间的变化关系，相关结论可为实际工程提供理论参考。

3．1 仿真条件

假设目标初始速度为（15m／s，15m／s），加速度为（1m／s2，1m／s2），雷达1和雷达2系统估计误差分别为（20m，2e－3rad）和（30m，3e－3rad），量测噪声方差分别为（15m，1e－3rad）和（30m，1．5e－3rad），过程噪声功率谱密度qx＝qy＝5m2／s3。雷达扫描周期同为1s，共采样1 000个点。

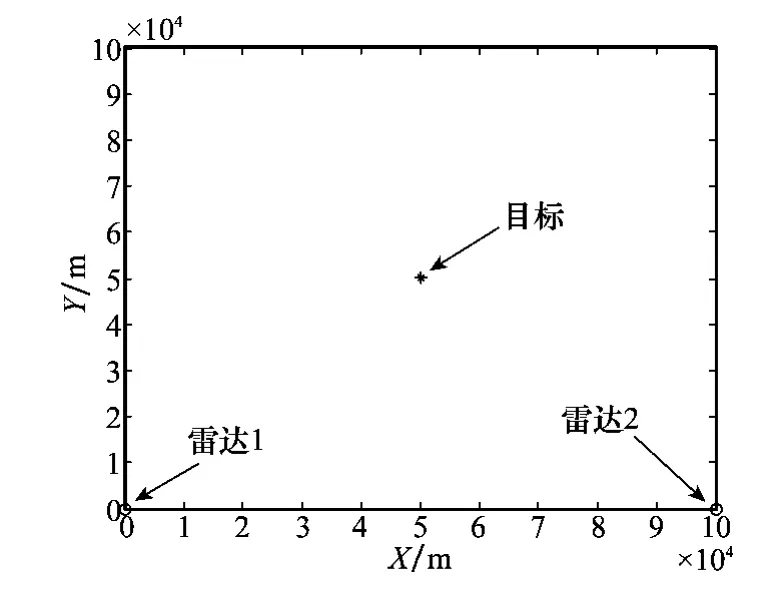
图1 多平台传感器与目标位置

3．2 仿真结果

采用蒙特卡罗仿真实验方式，仿真次数为200次。机动频率α分别取1／20，1／60和1／100。3种机动频率对应的雷达1和雷达2距离向量测误差在图2中给出。

图2（a）和图2（b）给出了不同机动频率对应的距离向误差配准均方根关于采样点仿真图。从图中可以发现随着采样点数的增加，蓝线与红线接近于重合，说明机动频率越大，误差配准均方误差越大，而当机动误差达到一定程度，均方误差趋于一致。显然较小的机动频率更加有利于系统误差配准。

图2（c）和图2（d）给出了不同机动频率对应的误差配准在方位向上均方误差仿真图。从图中可以得到与距离向相似的结论。同样随着采样点数的增加，较小的机动频率对应的误差配准均方误差越来越小，α＝1／60与α＝1／100均方误差在采样点超过300个时接近一致。所以较小的目标机动频率更加有利于系统误差配准操作，而较大的目标机动频率较之误差较大。

分析目标机动频率与系统误差配准关系具有很重要的实际意义。通常机动频率表示目标机动时间常数τm的倒数，其值取决于目标机动持续的时间，通常取经验值。当目标机动时间常数τm增加时，SINGER模型将趋近于匀加速运动模型，而当常数τm减小时，趋近于匀速模型。

根据本文结论匀加速运动模型将更加有利于系统误差配准的操作，而匀速运动模型的系统误差配准相对更加困难。造成这种现象的原因在于：对于匀加速运动模型，系统误差可以通过加速度、速度和位置等目标状态进行估计进而配准补偿，但是对于匀速运动模型其系统误差仅通过速度和位置两个状态反映，而对于实际目标跟踪系统，目标速度通常变化，系统误差在匀速运动模型条件下配准不够准确，在匀加速运动模型更加准确。

同时对于转弯机动目标其机动频率通常在1／60的小区间内变化，逃避机动目标其机动频率大约在1／20附近震荡，大气扰动机动频率通常为1。根据本文结论对于转弯机动目标跟踪系统误差配准相对容易，对于大气扰动造成系统误差配准更加复杂。造成该现象的内在原因分析将是团队下一步重点研究内容。

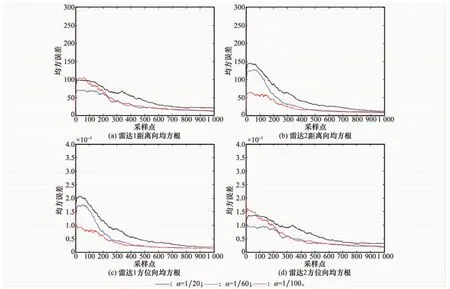
图2 误差配准均方误差

4 结 论

本文研究了基于SINGER运动模型的系统误差配准的扩维卡尔曼滤波方法，并讨论了不同机动频率对应的系统误差配准均方误差，得到了不同机动频率对应均方根误差的规律。但是较大机动频率对应较大配准误差结论的内在本质仍然需要从内在规律入手进行更加深入的研究，进而探究目标机动运动对于系统误差配准的本质影响。

［1］He Y，Xiu J J．Radar data processing with applications［M］．3rd ed．Beijing：Electronic Industry Press，2013．（何友，修建娟．雷达数据处理及应用［M］．3版．北京：电子工业出版社，2013．）

［2］Chen L，Wang G H，He Y，et al．Analysis of mobile 3－D radar error registration when radar sways with platform［J］．Journal of Navigation，2014，67（3）：451－472．

［3］Farina A，Studer F A．Radar data processing［J］．Research Studies LTD，1985（3）：325－339．

［4］Burke J J．The sage real time quality control function and its interface with buic II／buic III［R］．Bedford：MITRE Corporation，1996．

［5］Cui Y Q，Song Q，He Y．Performance comparison and analysis of three real－time registration bias estimation algorithms［J］．Fire Control and Command Control，2011，36（9）：55－59．（崔亚奇，宋强，何友．三种实时误差配准算法性能分析与比较［J］．火力与指挥控制，2011，36（9）：55－59．）

［6］Singer R A．Estimating optimal tracking filter performance for manned maneuvering target［J］．IEEE Trans．on Aerospace and Electronic Systems，1970，6（4）：473－483．

［7］Chen L Y，He J Z，Pan J H，et al．Study of multi－sensor range system bias estimation algorithm and simulation analysis［J］．Journal of System Simulation，2013，25（10）：2509－2514．（陈林元，何佳洲，潘江怀，等．多传感器距离误差配准算法研究及仿真分析［J］．系统仿真学报，2013，25（10）：2509－2514．）

［8］Boer Y，Driessen J N．Multi－target particle filter track before detect application g［J］．IEE Proceedings Radar，Sonar and Navigation，2004，151（6）：351－357．

［9］He Y，Wang G H．Multisensor information fusion with applications［M］．2nd ed．Beijing：Electronic Industry Press，2007．（何友，王国宏．多传感器信息融合及应用［M］．2版．北京：电子工业出版社，2007．）

E－mail：110988068＠qq．com

张 靖（1975－），女，高级工程师，博士，主要研究方向为信息融合、航迹关联。

E－mail：15652540242＠163．com

Real－time error registration algorithm and analysis based on the SINGER model

LI Yang，ZHANG Jing
（China Academy of Electronics and Information Technology，Beijing 100041，China）

System error registration plays a key role in the target track with multi－platform multi－sensor，which can estimate and compensate the system error of radar track．If without the accurate system error registration，the target track with multi－platform multi－sensor might generate an error or multi－tracks and cause the system track performance deterioration．An augmented Kalman filter is proposed to compensate the system error based on the target SINGER model，while the relation between the error registration accuracy and maneuvering frequency is also discussed by a simulated experience which provides a helpful theory for the system error registration in the target track with different maneuvering frequencies．

error registration；SINGER model；augmented Kalman filter；track association

TN 953

A

10．3969／j．issn．1001－506X．2015．06．05

李 洋（1983－），男，工程师，博士，主要研究方向为信息融合、误差配准。

1001－506X（2015）06－1255－04

2014－07－18；

2014－10－23；网络优先出版日期：2014－11－21。

网络优先出版地址：http：／／www．cnki．net／kcms／detail／11．2422．TN．20141121．0929．003．html