利用SIFT特征联合匹配的非刚体目标跟踪算法
侯志强,黄安奇,余旺盛,刘 翔
(空军工程大学信息与导航学院,陕西西安710077)
利用SIFT特征联合匹配的非刚体目标跟踪算法
侯志强,黄安奇,余旺盛,刘 翔
(空军工程大学信息与导航学院,陕西西安710077)
为了解决非刚体目标跟踪过程中由目标形状快速变化带来的困难,提出了利用SIFT特征联合匹配的非刚体目标跟踪算法。首先分别提取目标模板和当前搜索区域的SIFT特征点;然后利用改进的联合匹配策略在目标模板和当前搜索区域之间进行特征匹配;最后根据匹配结果确定目标在当前帧的位置和尺度。改进的联合匹配策略在构建相似度矩阵时,不但利用了具有旋转和尺度不变性的SIFT特征向量,并且充分考虑了特征点的空间位置信息,有效提高了特征匹配的准确性。将这种改进的联合匹配策略成功地引入到SIFT匹配跟踪中,克服了传统SIFT匹配算法用于非刚体目标跟踪时的缺陷。实验结果表明,该算法对目标的非刚性形变、尺度变化以及背景干扰都具有较强的鲁棒性。
视觉跟踪;非刚体目标;SIFT特征;联合匹配
0 引 言
视觉跟踪问题是计算机视觉领域中的一个重要问题,近年来被越来越多的学者所关注[1]。由于非刚体目标在运动过程中形状和外观都会不断发生变化,从而使得对非刚体目标的跟踪任务更具挑战性。如何对运动目标建立一个简单、准确、有效的外观模型是解决非刚体目标跟踪问题的关键。从选取模板形式的不同,可以将典型的非刚体目标跟踪算法分为以下几类:基于规则模板的跟踪、基于变形模板的跟踪、基于局部分块的跟踪和基于特征匹配的跟踪。目前已有大量基于规则模板的算法用于非刚体目标的跟踪中。经典的Mean Shift算法[2]对简单场景下的非刚体目标可以实现准确有效的跟踪,但是对遮挡和背景干扰比较敏感,算法容易收敛到局部极值。文献[3]通过偏最小二乘分析,使用在线学习获得的多个表观模型对目标进行描述。该算法由于同时利用了在线学习的目标及背景信息,能够有效地减少跟踪漂移问题。文献[4]利用推土机距离(earth mover’s distance,EMD)提出了一种新的目标变化概率模型,并将其应用到跟踪中。该算法针对刚体目标和非刚体目标都能取得较好的跟踪性能。非刚体目标也可以使用参数化的变形模板来构建目标模型,例如常用的主动轮廓模型(active contour models,ACM)[5]非常适合可变形目标的跟踪。但是这类参数化模型的数学描述往往比较严格,并且这类算法耗时严重,从而限制了它们的使用。水平集算法作为一种可实现对目标的精确分割与跟踪的理论框架也已经成功应用到非刚体目标的跟踪中[6]。基于局部分块的跟踪算法在对非刚体目标进行跟踪时也表现出了较为出色的跟踪性能[7-8]。文献[8]在对目标进行分块表示时利用了目标前景与背景间的差异信息,使得该算法对遮挡和背景干扰都具有较好的鲁棒性。利用目标的特征点来进行建模是解决非刚体目标跟踪的另一种思路,常用的特征点有角点[9]和SIFT特征点[10]等。文献[11]通过提取目标的局部特征点来进行表观特征描述,并利用传统的特征匹配策略进行跟踪。然而这种传统的特征匹配跟踪算法需要建立单个特征之间的对应关系,再通过求解仿射模型来确定跟踪结果。该方法受非刚体目标特征点空间位置的变化扰动较大,因此跟踪效果较差。文献[12]针对传统匹配跟踪算法的缺陷,提出一种联合匹配策略,将目标的局部特征集合看作一个整体并利用整体匹配最优的原则来实现特征匹配。该算法实时性较好,对目标的非刚性形变适应性较强。但是该算法提取的Harris角点不具有尺度不变性,在尺度变化剧烈的情况下,会导致匹配点的数量明显减少。同时该算法采用的灰度直方图对光照变化以及背景干扰也都比较敏感,且该算法忽略了特征点重要的空间位置信息,容易发生误匹配。
综合考虑以上算法的优缺点,本文提出一种利用SIFT特征联合匹配的非刚体目标跟踪算法。相对于文献[12],本文在特征点的描述和相似度矩阵的构造上更具优势。首先在特征点的描述上采用SIFT特征,增强了特征点的旋转和尺度不变性以及抑制背景干扰的能力;然后通过考虑特征点的空间信息,对原始的相似度矩阵进行了改进,进一步提高了抗干扰能力和匹配准确性。相对于传统的SIFT匹配跟踪算法,本文由于采用了联合匹配策略,能够有效地处理目标的非刚性形变。
1 基于SIFT特征的表观模型构建
1.1 SIFT特征提取
SIFT特征是图像的局部特征,该特征对旋转、尺度缩放、亮度变化保持不变性,对视角变化、仿射变换、噪声也保持一定程度的稳定性。而文献[12]使用的Harris角点只对旋转具有不变性,而对于尺度不具有不变性。如图1所示,目标原来的角点在尺度变大后变成了边缘点,表明Harris角点不具有尺度不变性。

图1 Harris角点不具有尺度不变性
SIFT算法依据其提出的高斯差分(difference of Gaussian,DOG)算子提取图像在不同尺度上的特征点,利用具有不同均方差参数σ的高斯函数G(x,y,σ)将一帧图像扩展到尺度空间的一系列图像。特征点通过对相邻尺度2幅图像的差分D(x,y,σ)求局部极值得到,即

式中,L代表图像的尺度空间;I(x,y)代表图像在位置(x,y)处的像素值,二维高斯核函数为
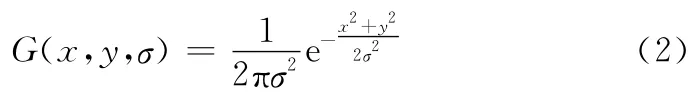
式中,σ代表高斯正态分布的均方差,称为尺度空间因子。在极值点所处的位置和尺度上,利用2×2的Hessian矩阵H作为稳定性判别标准剔除不稳定的特征点,以增强匹配稳定性、提高抗噪声能力。然后利用特征点邻域像素的梯度方向分布特性为每个特征点指定方向信息,并为每个关键点生成l=128维的SIFT特征向量。将目标模板的特征点集合记为{p1,p2,…,pm},对应的特征向量集合记为{sp1,sp2,…,spm}。
1.2 目标模型表示
首先在初始帧手动选择目标模板,此处模板为略大于目标的矩形;然后提取目标模板的SIFT特征。目标模型的具体表示如图2所示。

图2 目标模型表示样例
至此,目标的表观模型可表示为P={(p1,sp1),(p2,sp2),…,(pm,spm)}。
2 基于SIFT特征的联合匹配
文献[10]提出用Hough变换提取至少3对稳定匹配的关键点对,然后构建匹配点之间的仿射模型,通过求解模型的最小二乘解来确定参数。这种传统的SIFT匹配算法用在刚体目标的图像配准中能够取得良好的效果,然而当目标发生非刚性形变时,由Hough变换提取的稳定特征匹配数目可能少于3对,此时仿射模型便无法求解。并且,由非刚体目标形变引起的匹配点对之间相对位置的变化,会对仿射模型造成很大的扰动,最终导致较大的跟踪误差。
因此,本文借鉴文献[12]中联合匹配的思想,将目标模型中的所有SIFT特征点当作一个整体,通过整体匹配最优的原则来确定SIFT特征点之间的匹配关系。在构建相似度矩阵时,不但考虑了SIFT特征向量之间的相似度,并且加入了特征点的空间位置信息,有效地减少了误匹配。本文进行SIFT特征匹配的思路为:首先构建相似度矩阵;然后根据相似度矩阵将关键点的匹配问题转化为平衡指派问题;最后通过确定使整体效益最优的指派来确定关键点之间的匹配关系。
2.1 构建相似度矩阵
设目标表观模型为P={(pi,spi),当前搜索区域对应的表观模型为Q={(qj,sqj)。在联合匹配策略中,使用Bhattacharyya系数来量测SIFT特征向量之间的相似度,即点pi与qj之间的SIFT特征相似度为
特征点集的离散程度反映了目标的尺度大小,为了进一步减少背景中的孤立特征点对特征匹配的干扰,提高跟踪稳定性,引入距离约束对特征匹配的精度进行优化。设点qj与目标在上一帧的中心位置()之间的欧氏距离为:,则点pi与qj之间的距离相似度定义为


则点pi与qj之间的总体特征相似度为

式中,a为控制巴氏系数与距离约束比例关系的系数。计算出所有关键点之间的相似度,则相似度矩阵可表示为

对相似度矩阵进行归一化处理,使其满足标准的最优化模型求解条件,其公式为

式中,ρmax和ρmin分别表示相似度矩阵ρ中元素的最大值和最小值,相似度矩阵R中的元素用rij表示。
2.2 匹配关系模型的建立与求解
对目标模型中任意的pi=(i∈{1,…,m}),在当前搜索区域中找到与之匹配的qj=(j∈{1,…,n}),并且要求pi与qj之间的特征相似度rij之和最大。这是一类典型的指派问题,可以将其描述为0-1规划问题,即

式中,xij为匹配决策变量,当pi与qj匹配时,xij=1;否则,xij=0。
上述模型描述的问题为非平衡指派问题,可以通过在矩阵R中加入0元素将其转化为平衡指派问题。此时,式(8)所描述的模型可转化为标准的平衡指派问题模型:

上述模型可以用匈牙利算法(Hungarian algorithm,HA)[13]进行求解。
3 算法总结
3.1 算法描述
首先确定目标在当前帧的搜索区域,考虑目标运动过程在空间上的连续性,将搜索范围设定为以上一帧跟踪结果为中心的2倍于目标区域的范围。搜索区域的设定大大减少了SIFT特征变换的计算量。
将本文算法与文献[12]算法进行对比,来验证本文算法在特征点描述上更具鲁棒性。为保证实验对比的公平性,此处2种联合匹配策略都未加入距离约束。如图3所示,其中图3(a)和图3(c)为文献[12]基于Harris角点特征的匹配结果,图3(b)和图3(d)为本文基于SIFT特征的匹配结果。由图3(a)和图3(b)的对比结果可知,当目标的非刚性形变较大时,角点特征的稳定性较差,目标在当前帧的匹配点聚集在目标的局部区域。由图3(c)和图3(d)的对比结果可知,基于Harris角点特征的匹配策略容易受背景中灰度相似目标的干扰。而基于SIFT特征的匹配策略对于剧烈的非刚性形变和灰度相似目标干扰,都具有较强的鲁棒性。

图3 不同局部特征的匹配结果对比
在构建目标模型与当前帧候选模型的相似度矩阵时,通过引入距离约束来充分考虑特征点的空间位置信息,有效提高了抑制背景干扰的能力,降低了误匹配的概率。需要特别说明的是,由于联合匹配策略是通过整体匹配最优的原则来确定特征点之间的匹配关系,而不是点到点的严格匹配,因此这里所说的误匹配是指目标模板上的特征点匹配到当前帧背景上的特征点。为了验证引入距离约束对提高匹配精度的有效性,进行如下对比。同样,为了保证实验对比的公平性,本文联合匹配策略所使用的特征检测子与原始联合匹配策略一样,均使用Harris角点检测子。如图4所示。

图4 距离约束对匹配结果的影响
传统的SIFT特征匹配追求点到点的严格匹配,这对于刚体目标来说一般会得到精度较高的匹配结果。对于非刚体目标,由于目标不断发生着严重的非刚体形变,使用传统的SIFT特征匹配将难以得到足够的特征匹配点并容易产生误匹配。对此,本文首次将改进的联合匹配策略应用到SIFT特征匹配中。图5(a)为使用传统SIFT特征匹配策略的匹配结果,由于剧烈的非刚性形变使得成功匹配的特征点数量很少,且容易产生误匹配。图5(b)为使用本文联合匹配策略的匹配结果,成功匹配的特征点数量很多,且没有产生误匹配。

图5 特征匹配策略对比
在特征联合匹配完成后,根据特征点集分布的离散程度来确定最终的跟踪结果。本文以中心坐标(x,y)和目标尺度(h,w)来描述跟踪结果。假设目标的初始位置和尺度分别为为所有特征点的坐标均值。目标在当前帧的坐标位置为)为特征联合匹配得到的特征点坐标的均值。
当目标的尺度发生变化时,其内部特征点坐标的方差也相应发生变化,目标缩小时方差随之变小,目标变大时方差随之变大。据此,可通过特征点坐标方差之间的比例关系将当前目标的尺度描述为(σxkh0/σx0,σykw0/σy0)。其中,(σx0,σy0)为模板特征点坐标的方差,(σxk,σyk)为联合匹配所得特征点坐标的方差。图6(a)为特征联合匹配的结果,图6(b)为目标跟踪结果的最终描述。

图6 跟踪结果的最终描述
3.2 算法步骤
本文算法步骤的具体描述如下。
步骤1 在初始帧手动选择目标模板,并提取目标模板的SIFT特征来构建目标的表观模型
步骤2 读入新的视频帧,并在当前搜索区域内提取SIFT特征来构建当前搜索区域的表观模型
步骤3 依据联合匹配策略,对提取的SIFT特征进行联合匹配。
步骤4 依据特征联合匹配的结果,确定目标的位置和尺度,并输出当前帧的跟踪结果。
步骤5 对目标的位置和尺度信息进行更新,并反馈到步骤2,进行下一帧的跟踪。
4 实验结果与分析
本文的仿真环境为:Intel G1610CPU,2G内存,Windows XP系统,MATLAB 7.12.0。对6组常用的非刚体目标视频序列进行了跟踪测试,并与目前优秀的算法进行了对比分析,包括PLS[3],LOT[4]和TUJM[12]。目标的真实位置和尺度通过手工标定得到,图7所示为对非刚体目标进行标定的样例。为了便于对比分析,且保持结论的一般性,本文在测试算法性能时,目标模板的初始化是相同的。

图7 非刚体目标标定样例
4.1 Cartoon视频序列
如图8(a)所示,本段视频序列中的运动目标在形状、尺度和外观上都发生着快速、剧烈的变化。PLS算法不能适应目标的快速变化以及背景特征的干扰,很快便丢失目标(从第25帧开始)。LOT算法在目标急速运动时也出现了丢失目标的情况(25~95帧)。TUJM算法和本文算法采用联合匹配策略进行特征匹配,使得算法能够适应目标的快速变化。相比TUJM算法,本文算法提取的SIFT特征点数目更多且更加稳定,匹配结果更加准确。
4.2 Skaters视频序列
本组实验包含2组视频(Skater1序列和Skater2序列)。其中Skater1视频序列的跟踪结果如图8(b)所示。PLS算法能够有效地抑制背景元素,但是跟踪框逐渐收敛到了目标的中心位置。LOT算法在目标形变剧烈的情况下,跟踪结果也出现较大偏差,如第88帧。TUJM算法和本文算法都实现了对目标的有效跟踪,本文算法在尺度适应上具有更大优势。相比Skater1视频序列,Skater2视频序列的跟踪场景更加复杂,不但有大量与目标特征相似的背景元素的干扰(225帧),而且有跟踪视角的快速切换(从373~374帧),如图8(c)所示。其他3种算法显然不能够有效地解决这些困难,而本文算法成功地完成了跟踪任务。
4.3 Dancers视频序列
本组实验的2组视频展示了2种风格不同的舞蹈(Dancer1序列和Dancer2序列),如图8(d)和图8(e)所示。Dancer1视频序列的跟踪场景较为简单,但目标依然存在尺度和外观的不断变化,本文算法相比其他3种算法能够更加有效地处理这些难题。相比Dancer1视频序列,Dancer2视频序列中目标的形变以及尺度变化更加快速、剧烈。PLS算法不能正确地适应目标的尺度变化。LOT算法能够自动估计目标中存在的局部无序特征(local disorder,LD),并利用这些特征信息对目标实施有效的跟踪,得到了较为准确的跟踪结果。TUJM算法由于提取的Harris角点特征不具有尺度不变性,在目标形变剧烈的时候,匹配的特征点会明显减少,造成跟踪漂移(57~60帧)。本文算法提取的SIFT特征点具有良好的尺度不变性,因此在目标尺度变化剧烈的情况下,依然能够对目标实施准确、鲁棒的跟踪。

图8 跟踪算法性能的定性比较
4.4 Deer视频序列
如图8(f)所示,本段视频序列的背景特征与目标特征十分相似,且目标运动速度很快。LOT算法由于不能适应目标的快速运动和抑制背景特征的干扰,导致跟踪框很快发散。PLS算法和TUJM算法由于不能正确地区分目标特征和背景特征,导致跟踪出现较大偏差。而本文算法采用的SIFT特征在匹配时能够很好地抑制背景元素的干扰,匹配结果更加准确。
4.5 定量分析
为了定量地评价跟踪算法的性能,本文采用中心位置误差和覆盖率2项标准来对以上4种算法的跟踪结果进行比较。图9和图10分别展示了各个算法在跟踪视频序列时的中心位置误差和覆盖率,同时表1和表2给出了各个算法的平均中心误差和平均覆盖率(其中,粗体展示的是最优结果,粗斜体展示的是次优结果)。由定量分析可知,PLS算法的跟踪误差最大,覆盖率最低;TUJM算法和LOT算法在个别视频序列下的跟踪误差较大,覆盖率较低;而本文算法在各个视频序列下的跟踪结果都比较理想。

图9 中心位置误差比较

表1 目标平均中心位置误差比较
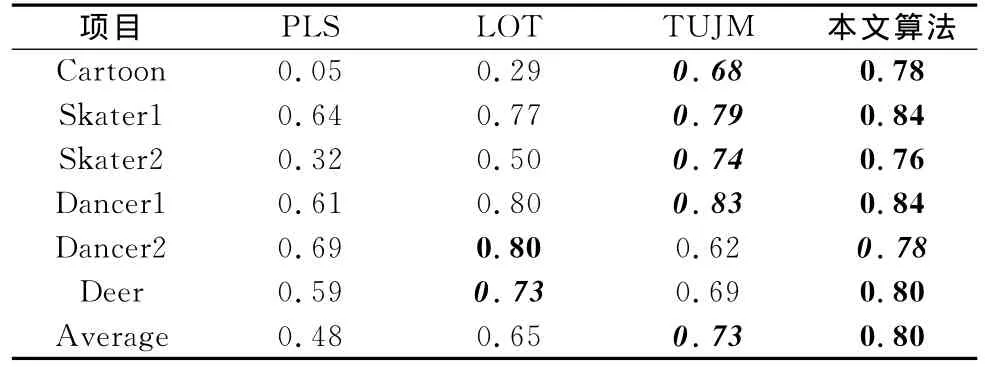
表2 目标平均覆盖率比较
PLS算法本质上属于基于分类的跟踪算法,通过对前景元素和背景元素进行采样并在线更新,构建一个鲁棒的分类器。该算法对刚体目标的跟踪性能较好,但是在跟踪非刚体目标时,很容易将跟踪框收敛到目标的局部位置。LOT算法通过将目标的表观信息和空间信息进行有效融合,提高了对非刚体目标的跟踪性能。但是当目标形变剧烈或是受到大量与目标特征相似的背景元素干扰时,跟踪性能明显下降,如图9和图10(a)和图10(f)所示。TUJM算法采用Harris算子进行关键点检测,并采用灰度特征进行描述,能够较好地适应非刚体目标的剧烈形变。但是Harris角点最大的缺陷在于其不具有尺度不变性,使得该算法提取的特征点不够稳定,特征点有时会集中在目标的局部位置,而且仅用灰度特征来描述关键点,很容易受到背景相似特征的干扰。相较于参考算法,本文采用SIFT特征对关键点进行描述,并有效利用了特征点的空间位置信息,使得该算法对目标的尺度变化、非刚性形变及背景干扰都具有较强的鲁棒性,最终取得了更加准确的跟踪结果。
6 结 论
针对非刚体目标的鲁棒跟踪问题,本文提出了一种利用SIFT特征联合匹配的非刚体目标跟踪算法。首先提取目标的SIFT特征点对目标模型进行描述,然后利用改进的联合匹配策略实现SIFT特征的匹配,最后根据匹配结果确定目标的位置和尺度。与原始的联合匹配策略相比,本文在特征点的描述和相似度矩阵的构造上都进行了改进,并通过详细的实验对比分析,验证了改进联合匹配策略的优势。相较于传统的SIFT匹配算法不适用于非刚体目标跟踪的问题,改进后的SIFT联合匹配算法能够很好地适应目标的非刚性形变,且对目标的尺度和旋转变化以及背景干扰,都具有较强的鲁棒性。通过与目前优秀的算法(stateof-the-art)进行对比,可以发现本文算法在跟踪精度和稳定性方面都具有较为出色的表现。需要指出的是:①本文算法在对更为复杂的背景条件和发生遮挡情况下目标的跟踪性能有待提高。②对SIFT特征点进行有效的在线更新也是影响跟踪性能的一个关键问题。下一步工作将着重解决这2个问题。
[1]Wu Y,Lim J,Yang M H.Online object tracking:a benchmark[C]∥Proc.of the Computer Vision and Pattern Recognition,2013:2411-2418.
[2]Comaniciu D,Ramesh V,Meer P.Real-time tracking of nonrigid objects using mean shift[C]∥Proc.of the Computer Vision and Pattern Recognition,2000:142-149.
[3]Qing W,Feng C,Wen L X,et al.Object tracking via partial least squares analysis[J].IEEE Trans.on Image Processing,2012,21(10):4454-4465.
[4]Shaul O,Aharon B,Dan L,et al.Locally orderless tracking[C]∥Proc.of the Computer Vision and Pattern Recognition,2012:1940-1947.
[5]Kass M,Witkin A,Terzopoulos D.Snakes:active contour models[J].International Journal of Computer Vision,1988,1(4):
321-331.
[6]Xiao C,Gan J,Hu X.Fast level set image and video segmentation using new evolution indicator operators[J].The Visual Computer,2013,29(1):27-39.
[7]Adam A,Rivlin E,Shimshoni I.Robust fragments-based tracking using the integral histogram[C]∥Proc.of the Computer Vision and Pattern Recognition,2006:798-805.
[8]Nejhum S M S,Ho J,Yang M H.Online visual tracking with histograms and articulating blocks[J].Computer Vision and Image Understanding,2010,114(8):901-914.
[9]Harris C,Stephens M.A combined corner and edge detector[C]∥Proc.of the Fourth Alvey Vision Conference,1988:147-151.
[10]Lowe D.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[11]Hare S,Saffari A,Torr P H S.Efficient online structured output learning for keypoint-based object tracking[C]∥Proc.of the Computer Vision and Pattern Recognition,2012:1894-1901.
[12]Yu W S,Hou Z Q,Tian X H,et al.Non-rigid object tracking using joint matching of local features[J].Journal of Xidian U-niversity,2014,41(6):183-189.(余旺盛,侯志强,田孝华,等.利用局部特征联合匹配的非刚体目标跟踪[J].西安电子科技大学学报,2014,41(6):183-189.)
[13]Kuhn H.The Hungarian method for assignment problem[J].
Naval Research Logistics,2005,2(1):7-21.
E-mail:hou-zhq@sohu.com
黄安奇(1988-),男,硕士研究生,主要研究方向为视觉跟踪。
E-mail:13319270512@163.com
余旺盛(1985-),男,博士研究生,主要研究方向为图像分割、视觉跟踪。
E-mail:xing_fu_yu@sina.com
刘 翔(1990-),男,硕士研究生,主要研究方向为视觉跟踪。
E-mail:liu_xiang000@126.com
Non-rigid object tracking based on joint matching of SIFT features
HOU Zhi-qiang,HUANG An-qi,YU Wang-sheng,LIU Xiang
(Information and Navigation Institute,Air Force Engineering University,Xi’an 710077,China)
To solve the problems in non-rigid object tracking,such as the significant and rapid variation in shape as well as appearance,an efficient tracking algorithm based on joint matching of SIFT features is proposed in this paper.Firstly,local SIFT key points of the object template and the current searching area are detected and described.Then,the key points are matched via the improved joint matching strategy,and the right matching pairs are picked out.Finally,the object’s location and size are calculated according to the matching results.When constructing the similarity matrix,the improved joint matching strategy exploits the rotation and scale invariance of SIFT features,and considers the spatial information of the key points,which effectively enhances the feature matching accuracy.This paper successfully introduces the improved matching strategy to the SIFT matching tracking,which overcomes the defect of the traditional SIFT matching algorithm in non-rigid object tracking.The experimental results indicate that the proposed algorithm is robust to object’s non-rigid deformation,scale change and background distraction.
visual tracking;non-rigid object;SIFT feature;joint matching
TP 391.4
A
10.3969/j.issn.1001-506X.2015.06.29
侯志强(1973-),男,教授,博士,主要研究方向为图像处理、计算机视觉和信息融合。
1001-506X(2015)06-1417-07
2014-01-21;
2014-06-27;网络优先出版日期:2014-11-05。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20141105.1633.015.html
国家自然科学基金(61175029,61473309);陕西省自然科学基金(2011JM8015)资助课题

