鲁棒原子范数降噪及其在线谱估计中的应用

王洁洁，张建秋

（复旦大学电子工程系，上海200433）

鲁棒原子范数降噪及其在线谱估计中的应用

王洁洁，张建秋

（复旦大学电子工程系，上海200433）

针对测量数据中含有异常值的线谱估计问题，提出了一种对异常值鲁棒的原子范数降噪方法来提高线谱估计的性能。该方法构建了一个可以联合估计出异常值及原始信号的优化问题，并在代价函数中加入l1范数和原子范数惩罚项来分别对异常值的稀疏性和信号本身的特性进行约束。一旦获得了该优化问题的解，那么就可利用现有的算法对降噪后的信号进行线谱估计。仿真结果表明，在数据中存在异常值的情况下，所提的算法能够更准确地恢复原始信号，从而使降噪后的谱估计的精度和分辨率明显提高。

线谱估计；异常值；鲁棒降噪；原子范数；l1范数

0 引 言

从含噪声的采样数据中提取出信号的频率信息是统计信号处理中的一个重要问题。它在雷达目标波达角估计、传感器阵列信号处理以及图像处理等方面都有普遍的应用［1－3］。

一般地，对于由若干频率线性组合构成信号的线谱估计问题，通常假设其信号的采样数据叠加了高斯白噪声。为了获得更好的线谱估计结果，在利用一些常见的算法进行谱估计之前，可以先对测量数据降噪。对此，文献［4］提出一种原子范数降噪方法以及其在线谱估计中的应用，其理论和仿真结果均证明对数据首先进行降噪，然后再进行线谱估计，其估计结果远远优于现有对含噪声数据直接进行谱估计的结果。

可是在实际中，采样数据不一定符合文献［4］的信号模型假设。例如：在一些应用场景中，采样数据中除了符合文献［4］信号模型的有效数据之外，还存在着由测量者一时操作不当或仪器突然失常等因素导致的采样异常值［5－7］。目前，对于异常值，还没有严格的数学定义，一般认为的异常值是指与其他大部分数据差异较大的观测值。异常值的存在，往往意味着测量误差或者观测数据具有拖尾分布［8］。文献［8－9］的研究表明：含重尾噪声的数据与含高斯噪声的数据相比，其概率分布的拖尾较大，有较大的可能性产生与均值差异较大的观测值。这样的观测值在统计特性上与含有异常值的数据十分相似，因此这类数据也常常被认为是含异常值的数据。一般考虑的重尾分布包括高斯混合模型（Gaussian mixture model，GMM）和α－稳定分布等。

为了对存在异常值的数据进行降噪，在本文中将异常值视为一未知的辅助变量，并考虑信号本身的特性，构建了一个对含异常值数据降噪的优化问题，该问题利用l1范数正则项对异常值的稀疏性进行约束［5，10］，期待以此去除异常值对降噪过程的影响，进而获得信号的鲁棒估计。分析表明本文提出的优化问题有如下优点：①可以同时处理测量数据中的异常值和高斯背景噪声；②不需要已知异常值的分布；③在测量数据中仅叠加有高斯噪声的情况下依然有效。在此基础上，可以利用现有算法［11－14］对降噪后的信号进行线谱估计。仿真结果表明：在测量数据含有异常值的情况下，本文提出的鲁棒降噪方法能够更准确地恢复原始信号，此时利用谱估计算法得到的线谱估计精度和分辨率都明显优于现有方法。

1 信号模型

考虑信号模型

式中，y＝［y1，y2，…，yN］T表示测量数据矢量；o是具有稀疏特性的异常值矢量，它有I个非零元素，对应于观测数据中的异常值，且有可能为较大的值；n为N×1的零均值高斯白噪声矢量；表示由K个频率成分构成的原始信号，A＝［a1，a2，…，aK］为频率导向矩阵，且

式中，ωk表示频率；｛tn＝nT′｝Nn＝1表示均匀的采样时刻，T′为采样周期；s＝［s1，s2，…，sK］T为信号K个频点的复幅度。

在测量信号y存在异常值的谱估计中，如果能在去除测量数据中异常值的同时，对含有噪声的信号进行降噪，进而获得期待的有效数据，那么显然利用这样获得的有效数据，可更准确地估计出信号的频谱信息。下面讨论获取这种有效数据的方法。

2 鲁棒原子范数降噪的谱估计方法

2．1 原子范数简介

首先，简单介绍一下原子范数的定义［4］。假设信号g为一集合A⊂CN中若干元素的非负线性组合，则信号g的原子范数‖g‖A定义为

式中，inf｛V｝为集合V的下确界；conv（V）为集合V中点的凸包。原子范数是一个抽象而丰富的概念，在不同的场合中有不同的意义，但其本质是约束信号中的某种稀疏特性［4］。例如：如果将原子范数作为惩罚项纳入稀疏矢量估计问题，它将表现为l1范数，而在低秩矩阵恢复中它则为核范数。

2．2 基于鲁棒原子范数的降噪算法

测量异常值通常具有稀疏特性［5－7］，如果同时考虑待恢复信号和信号采样数据异常值的稀疏性，而希望恢复的信号尽可能准确，那么可以描述为优化问题P1

式中，‖o‖0为非凸l0范数，即矢量o的非零元素个数；‖x‖A为信号x的原子范数；λ0和τ均为正则化参数。下面具体分析优化问题P1的合理性以及对异常值的鲁棒性能。

首先是合理性。在优化问题P1中，x为期待恢复的信号，而式（3）中的第一项则表示观测数据与恢复的信号x以及异常值o之和的误差应该尽可能地小，由于y－x－o符合高斯分布，即该项也对应高斯噪声场景下的线性回归问题。第二项中，利用l0范数正则项对异常值的稀疏性进行了约束，通过正则化参数λ0来控制异常值的稀疏度，即：如果测量数据中的异常值越少，那么λ0的值应该取更大的值，以强调异常值的稀疏性对问题P1的影响，反之亦然。第三项则通过原子范数惩罚项约束了问题中信号本身的特性。由此可以看出，提出的优化问题P1同时处理了数据中的异常值以及背景噪声以恢复原始信号。

当测量数据中不包含异常值，即测量数据中仅含高斯白噪声时，该优化问题依然可以有效地降噪。此时，通过取参数λ0为较大的值，则可以使待求解优化问题P1得到的异常值元素几乎全部为0。此时优化问题将退化成P2

P2描述问题就是文献［4］不含异常观测数据的降噪问题。由于优化问题P2试图通过拟合带异常值的观测数据来估计原始数据，因此当测量数据中包含异常值时，该算法已经失效。为分析本文算法的鲁棒性能，先对本文提出的优化问题进行简化。

在谱估计场景中，信号是频率导向矢量的非负线性组合，则信号的原子集为

其中

信号所对应的频率导向矢量集合subA＝｛a1，a2，…，aK｝为该原子集的真子集：subA⊂A。

此时，信号的原子范数［4］可以表示为

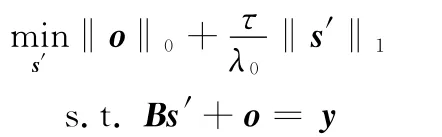
式中，B为信号的原子集A中的原子构成的N×P矩阵，由于A为无限集，因此在此问题中P为无穷大；s′为稀疏矢量，其非零值对应原始信号K个频点的复幅度；‖s′‖1为s′的l1范数

式中，sa为频点对应的信号幅度。将式（4）代入问题P1中，可以得到P1的等价问题P3

对于该优化问题有如下命题成立［15］：

令s0∈CP，且‖s0‖0＝K，o∈CN，且‖o‖0＝I，B∈CN，P，N≤P，且B中每一列相互正交。假设y＝Bs0＋o＋n，o为稀疏矢量，其I个非零元素为较大值，n为零均值高斯白噪声矢量。如果满足N≥2×I＋（τ／λ0＋1）×K，则当τ／λ0≥1时，问题P3有唯一的解s＾′＝s0。

根据该命题，当满足上述条件时本文提出的算法能够在测量数据带异常值的情况下有效地估计出原始数据。

在对问题的简化过程中，构造了一个列维度无限大的矩阵。可以看出，采样原子范数对原始数据进行约束，与最小绝对值压缩方法（least absolute shrinkage and selection operator，LASSO）中的l1范数约束有相似的物理意义。两者都强调在一个较大的候选频率点集合中，信号包含的频率成分较少。不同的是LASSO问题中的候选频率点集合是离散有限的，而在原子范数相应的频率点集合中，频点f可以是［0，1］间的任意数值，因此是连续无限的［4］。这意味着在信号包含的频点没有落在LASSO问题中的候选频率点集合时，采用原子范数约束信号特性将会更准确。

通过上面的分析，可知本文提出的优化问题可以带来以下好处：①可以同时处理测量数据中的异常值和背景噪声；②不需要已知异常值的概率分布；③在测量数据中仅叠加有高斯噪声的情况下依然有效。

众所周知，式（3）基于l0范数的优化问题是非凸且多项式时间内不可解的NP－hard问题，因此可以松弛式（3）中的l0范数为l1范数约束［16］，以此得到多项式时间内可解的凸优化问题，即P4

式中，σes为估计得到的噪声方差［4］。在确定了τ后，参数λ1的确定仅依赖于异常值矢量的稀疏性，而与信号本身的约束无关，因此可以参考文献［5］中的方法进行选取。

2．3 算法的运算量分析

下面介绍该优化问题的解法。在谱估计问题中信号的原子范数［4］可以表示为正则化参数λ1控制。

需要注意的是，正则化参数λ1和τ的选取是否合适对本算法的性能有很大的影响。在优化问题P4中，若λ1的选取使得异常值矢量估计准确，则y－x－o符合高斯分布。此时本文的优化问题退化为文献［4］中不含异常值的数据降噪问题，那么，τ可以根据文献［4］中给出的方法确定：

式中，算子T（u）表示将矢量u作为第一列构成托普利兹矩阵；trace（M）表示矩阵M的迹。

将式（7）代入优化问题P4中，则得到

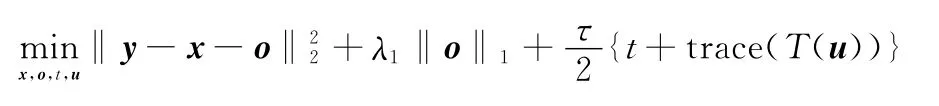
该问题可以采用常见的凸优化求解工具来求解，亦可以采用基于交替方向乘子算法（alternating direction method of multipliers，ADMM）的方法来提高算法的速度［17］。ADMM的思想是将总体问题分为若干子问题，通过子问题间的交叉迭代得到最终的解。下面具体分析本优化问题的求解过程。

重新书写上面的优化问题为

其拉格朗日函数为

式中，‖MC×D‖F为弗罗贝尼乌斯范数，为任意C×D矩阵。

则ADMM算法包含以下的更新步骤：

式中，l为迭代次数。

在第一步的更新过程中，再将优化问题分解为

式中，y′＝y－ol；y″＝y－xl＋1。

引入标记

则t，u，x，o的更新过程为

式中，W是对角矩阵，其对角元素为

T（u）的结果是第一列为u的托普利兹矩阵；而T＊（u）为T（u）的逆过程，称为托普利兹近似矢量。对于一个N×N的方阵U，其托普利兹近似矢量为N×1的矢量u［4］。e1＝［1，0，…，0］，N为观测数据的长度。

而算子S的表达式［15］为

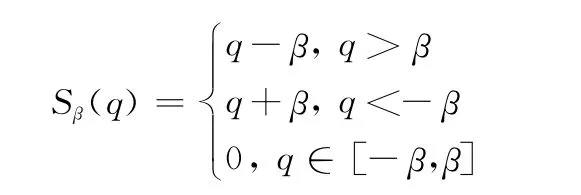
Z的更新过程需求解下述问题：

该问题的解相当于把矩阵M投影到正定椎体上。求解该问题只需简单地对M进行特征值分解，并将其负特征值置为0后重新合成新矩阵。这里矩阵M为

而Λ按照式（8）更新。

从上面的分析可以看出，每次迭代中，复杂度最高的运算为求特征值运算，因此本算法的复杂度取决于实际的求解特征值方法的复杂度。

在解优化问题P4后，得到降噪的数据序列y‴，则可以用迭代自适应算法（iterative adaptive approach，IAA）［11］，或者其他常见的算法［12－14］来进行谱估计。

3 仿真结果

3．1 仿真条件

在下面的仿真中，假设复数信号x中有K＝4个频率成分，分别是0．2Hz，0．62Hz，0．8Hz，0．82Hz。对应频点上的幅度为4V，3V，7V，3V。采样频率为2Hz，采样数据长度N＝65。下面构造两种观测数据来验证本文算法的鲁棒性：第一种仿真数据在原始信号上叠加异常值以及高斯白噪声；第二种仿真数据根据引言中提及的原因，在原始数据上直接叠加上重尾噪声。下面是两种仿真数据的具体构造过程。

3．1．1 在10%的数据上叠加异常值

数据模型为

式中，n为N×1的高斯白噪声矢量，均值为0，方差σ2由仿真过程中的信噪比（signal to noise ratio，SNR）和原始信号功率决定

式中，分子为原始信号的平均功率，E｛·｝表示求均值；η为信噪比。o为N×1的异常值矢量，只有N×10%的元素为非零值。这些非零元素是均值为零，标准差为10σ的高斯噪声，其位置随机均匀分布在数据序列中。可见异常值矢量是稀疏的，且非零值为较大的值，符合异常值的特性。｜z｜表示小于z的最大整数。

3．1．2 在原始数据中叠加上重尾噪声

（1）符合高斯混合模型的噪声

将o＋n统一合成噪声r。rn（n＝1，2，…，N）的概率密度函数为

（2）α－稳定噪声

α－稳定噪声是另外一种典型的重尾分布噪声。采用位置参数为0的对称α－稳定噪声（SαS）分布产生α－稳定噪声，其特征函数为

式中，参数α称为特征参数，α∈（0，2］。它决定该分布脉冲特性的程度，值越小，对应分布拖尾越厚，相反，值越大，分布拖尾越小［18］。高斯分布和柯西分布分别对应着α＝2和α＝1的情况。仿真中取α＝1．2，分散系数γ为

式中，x′n，j（n＝1，2…，N）为第j次实验恢复的数据序列；xn，j为第j次实验的原始信号。

频谱估计仿真图中MSE的计算方法为

本文仿真验证的算法性能包括两个方面：一是鲁棒原子范数降噪算法在数据有异常值的情况下对数据恢复的精度；二是利用恢复的数据进行谱估计的精度和分辨率。衡量标准为均方误差（mean square error，MSE）。

仿真图中的每个数据点由J＝60次仿真的结果求平均得到。在数据恢复仿真图中MSE的计算方法为

式中，f′k，j是第j次实验对真实频率点fk，j的估计。

算法中用到的正则化参数λ和τ根据第2．2节所述方法选取，ρ＝1。在本文仿真中，谱估计算法采用IAA算法。IAA方法迭代次数为15次。

3．2 仿真结果

为方便表述，下面用场景1，场景2和场景3分别指代针对第3．1．1节测量数据，第3．1．2节中（1）和（2）测量数据的仿真过程。

首先给出数据恢复的结果。图1～图3中，横坐标为SNR，范围为0～25dB；纵坐标为数据恢复MSE。从图中可以看出在场景1、场景2和场景3中本文提出的算法恢复原始数据的性能较原子范数降噪算法有较大的改进。而在α－稳定噪声，场景3中原子范数降噪的算法的效果很差，在SNR较低的情况下甚至已经失效。此外，随着SNR的提高，两种算法的恢复效果都有所提高，并且差距缩小。

图1 场景1下数据恢复MSE与SNR的关系

图2 场景2下数据恢复MSE与SNR的关系

图3 场景3下数据恢复MSE与SNR的关系

图4～图6分别为3个场景下直接进行IAA谱估计以及降噪后的IAA谱估计的MSE曲线。图中，横坐标为SNR，范围为0～25dB；纵坐标为频率估计MSE。从图中可以看到在这3种场景下本文提出的算法与直接用IAA算法以及原子范数降噪后的IAA算法相比较，频率估计的MSE明显降低，这说明本文算法对真实频率点的估计更为准确，精度提高。而原子范数降噪后的IAA在场景3下，当SNR较低时其效果甚至不如直接进行IAA谱估计的结果。此外，从图中也可以看出，IAA算法对异常值十分敏感，数据中少量的异常值都能使IAA算法的性能大幅下降。而随着信噪比的提高，3种处理方法的MSE性能同样都有所提高，且差距缩小。

图4 场景1下频率估计MSE与SNR的关系

图5 场景2下频率估计MSE与SNR的关系

图6 场景3下频率估计MSE与SNR的关系

最后以混合高斯噪声场景为例，给出SNR为5dB时3种处理方法得到的频谱图。在图7～图9中，横坐标为归一化频率，纵坐标为估计得到的频率点幅度。该频谱图由20次仿真得到的频谱求平均得到。从图中可以看到，在数据中有异常值的情况下，IAA谱估计结果主瓣较宽，旁瓣也较大。而本文的处理方法能够很好地抑制频谱泄漏，提高频谱估计的分辨率，更好地突出真实的频率成分。对比降噪前后IAA谱估计的结果可以看到，本文降噪方法能够有效地去除背景噪声。且从图7和图8中可以看到，IAA算法和原子范数降噪后IAA算法谱估计的频谱图中均出现伪峰。但是本文算法的缺陷是，对降噪后的数据进行IAA谱估计，在信噪比较低的情况下虽然对频率点估计更为准确，但对幅度的估计并不是很准确。在信噪比高的情况下该性能将有所改善。

图7 IAA算法的平均功率谱图

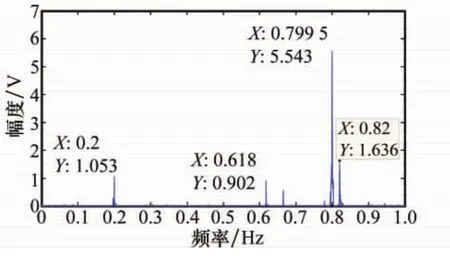
图8 原子范数降噪结合IAA算法的平均功率谱图

图9 鲁棒降噪结合IAA算法的平均功率谱图

4 结 论

针对观测数据中存在异常值的情况，本文提出了一种鲁棒的原子范数降噪方法，并将其应用于线谱估计问题。该方法构建了一个可以联合估计出异常值及降噪信号的优化问题，并在此优化问题中利用l1范数和原子范数分别对异常值的稀疏性和信号本身的特性进行约束。通过求解该优化问题，获得降噪后的有效数据，进而可利用现有的算法对降噪后的数据进行谱估计。该算法能够更准确地恢复原始信号，而且利用现有算法获得谱估计的精度和分辨率也有明显的提高。

［1］She Y Y，Wang J P，Li H H，et al．Group iterative spectrum thresholding for super－resolution sparse spectral selection［J］．IEEE Trans．on Signal Processing，2013，61（24）：6371－6386．

［2］Lin G，Huynh C P，Robles－Kelly A．Segmentation and estimation of spatially varying illumination［J］．IEEE Trans．on Image Processing，2014，23（8）：3478－3489．

［3］Malek－Mohammadi M，Jansson M，Owrang A，et al．DOA estimation in partially correlated noise using low－rank／sparse matrix decomposition［C］∥Proc．of the 8th IEEE Sensor Array and Multichannel Signal Processing Workshop，2014：373－376．

［4］Bhaskar B N，Tang G G，Recht B．Atomic norm denoising with applications to line spectral estimation［J］．IEEE Trans．on Signal Processing，2013，61（23）：5987－5999．

［5］Giannakis G B，Mateos G，Farahmand S，et al．USPACOR：universal sparsity－controlling outlier rejection［C］∥Proc．of the IEEE International Conference on Acoustics，Speech and Signal Processing，2011：1952－1955．

［6］Mateos G，Giannaikis G B．Robust PCA as bilinear decomposition with outlier－sparsity regularization［J］．IEEE Trans．on Signal Processing，2012，60（10）：5176－5190．

［7］Farahmand S，Giannakis G B，Angelosante D．Doubly robust smoothing of dynamical processes via outlier sparsity constraints［J］．IEEE Trans．on Signal Processing，2011，59（10）：4529－4543．

［8］Zeng W J，So H C，Huang L．lp－MUSIC：robust direction－ofarrival estimator for impulsive noise environments［J］．IEEE Trans．on Signal Processing，2013，61（11）：4296－4308．

［9］Chen Y，So H C，Sun W Z．lp－norm based iterative adaptive approach for robust spectral analysis［J］．Signal Processing，2014，94：144－148．

［10］Farahmand，Shahrokh．Distributed and robust tracking by exploiting set－membership and sparsity［EB／OL］．［2014－03－20］．http：∥purl．umn．edu／113021．

［11］Yardibi T，Li J，Stoica P，et al．Source localization and sensing：a nonparametric iterative adaptive approach based on weighted least squares［J］．IEEE Trans．on Aerospace and Electronic Systems，2010，46（1）：425－443．

［12］Zheng J M，Kaveh M．Sparse spatial spectral estimation：a covariance fitting algorithm，performance and regularization［J］．IEEE Trans．on Signal Processing，2013，61（11）：2767－2776．

［13］Stoica P，Babu P，Li J．SPICE：a sparse covariance－based estimation method for array processing［J］．IEEE Trans．on Signal Processing，2011，59（2）：629－638．

［14］Yan F G，Jin M．Low－complexity DOA estimation based on compressed MUSIC and its performance analysis［J］．IEEE Trans．on Signal Processing，2013，61（8）：1915－1930．

［15］Popilka B，Setzer S，Steidl G．Signal recovery from incomplete measurements in the presence of outliers［J］．Inverse Problems and Imaging，2007，1（4）：661－672．

［16］Gribonval R，Nielsen M．Sparse representations in unions of bases［J］．IEEE Trans．on Information Theory，2004，49（12）：3320－3325．

［17］Boyd S，Parikh N，Chu E，et al．Distributed optimization and statistical learning via the alternating direction method of multipliers［J］．Foundations and Trends in Machine Learning，2011，3（1）：1－122．

［18］Sadreazami H，Ahmad M O，Swamy M N S．A study of multiplicative watermark detection in the contourlet domain using alpha－stable distributions［J］．IEEE Trans．on Image Processing，2014，23（10）：4348－4360．

E－mail：12210720037＠fudan．edu．cn

张建秋（1962－），男，教授，博士，主要研究方向为信号处理及其在通信、控制、测量、图像和雷达中的应用。

E－mail：jqzhang01＠fudan．edu．cn

Robust atomic norm denoising with its applications to line spectral estimation

WANG Jie－jie，ZHANG Jian－qiu
（Department of Electronics Engineering，Fudan University，Shanghai 200433，China）

To estimate the line spectrum of data corrupted with outliers，a robust atomic norm denoising method is proposed．In the method，an optimization problem jointly estimating the outliers and the original signal is formulated．By adding an l1norm penalty on the outliers and an atomic norm penalty on the signal to the cost function，the sparsity in the outliers and the signal own characteristics are constrained．Once the optimization problem is solved，the existed spectral estimation algorithms can be used to estimate the spectrum of the denoised signal．The simulation results indicate that when the observed data are corrupted with outliers，the proposed method can acquire a more accurate original signal estimation，thus the spectral estimation will be of higher precision and resolution．

line spectral estimation；outliers；robust denoising；atomic norm；l1norm

TN 911．72

A

10．3969／j．issn．1001－506X．2015．06．04

王洁洁（1989－），女，硕士研究生，主要研究方向为信号处理及其应用。

1001－506X（2015）06－1249－06

2014－05－12；

2014－11－04；网络优先出版日期：2014－12－01。

网络优先出版地址：http：／／www．cnki．net／kcms／detail／11．2422．TN．20141201．1951．001．html

国家自然科学基金（61171127）资助课题