高阶运动目标的长时间相参积累算法

田 超，文树梁，杜智远

（1．北京无线电测量研究所，北京100854；2．中国人民解放军92493部队，辽宁葫芦岛125001）

高阶运动目标的长时间相参积累算法

田 超1，文树梁1，杜智远2

（1．北京无线电测量研究所，北京100854；2．中国人民解放军92493部队，辽宁葫芦岛125001）

针对具有任意阶运动的目标的长时间相参积累问题，提出一种基于多维非均匀快速傅里叶变换（non－uniform fast Fourier transform，NUFFT）的长时间相参积累算法。该算法先在快时间频域沿慢时间维利用多维NUFFT实现运动补偿，然后通过快速傅里叶逆变换（inverse fast Fourier transform，IFFT）最终实现相参积累。该算法积累性能接近理论最优且计算量小于已有算法。特别地，对于具有加加速度的运动目标进一步提出基于Wigner－NUFFT的相参积累算法，该算法相比多维NUFFT，计算量大大减小，但对积累前单个脉冲的信噪比提出更高要求。仿真结果证明了所提算法的有效性。

相参积累；非均匀快速傅里叶变换；高阶运动；运动补偿

0 引 言

隐身技术的广泛应用大大降低了雷达对新一代战机、导弹等目标的检测性能［1－2］，因此如何实现对这类雷达截面积较小的目标的检测已成为亟待解决的技术问题。利用长时间的信号积累是一种实现微弱运动目标检测的有效手段，其关键问题是如何实现目标回波的运动补偿［3－4］。现有积累算法多是针对匀速运动目标，但实际上目标往往具有加速度甚至更高阶的运动参数，这限制了一些算法的应用，而已有可用于高阶运动目标的积累算法主要分为非相参，相参与非相参混合以及相参3类。

非相参积累算法以Hough变换为代表，尽管文献［5－8］以处理匀速运动目标为例，但所提方法对具有高阶运动的目标同样适用，该方法运算量小，但低信噪比时性能下降明显。相参与非相参积累算法的主要思想是将回波数据分段，近似认为目标在段内进行匀速运动，从而利用快速傅里叶变换（fast Fourier transform，FFT）实现相参积累，段间则利用Hough变换进行非相参积累［9］，其低信噪比下的目标检测性能相比于文献［5］有所提高，其性能取决于帧内相参积累效果。相参积累算法以广义Radon傅里叶变换（generalized Radon Fourier transform，GRFT）为代表［10］，该算法与相参Hough变换思路有相似之处［11］，且更具一般性，其积累性能更优，但由于需要对各阶运动参数进行遍历搜索，运算量大。另外，匀速目标的相参积累中常用的Keystone变换和线性调频Z变换（chirp Z transform，CZT）在补偿掉因目标运动产生的高阶相位项后可以应用［12－14］，这种处理方式可很好地实现相参积累，但其计算复杂度仍难以满足实时处理的要求。

本文将非均匀快速傅里叶变换（non－uniform fast Fourier transform，NUFFT）推广到多维并将在快时间频域沿慢时间维进行目标回波运动补偿的问题转换为多维NUFFT（multi－dimensional NUFFT，MNUFFT）的计算问题，利用MNUFFT完成运动补偿后通过快速傅里叶逆变换（inverse fast Fourier transform，IFFT）完成相参积累。该方法对具有任意阶运动的目标均适用，积累性能可达到理论值，且运算量小于常用相参积累算法。特别针对具有加加速度的运动目标提出了基于Wigner－NUFFT（WNUFFT）的积累方法，该算法进一步减小了实现积累计算复杂度，但对积累前单个脉冲的信噪比亦提出更高要求。

1 各阶运动参数的分辨率

假设雷达发射的窄带信号为

式中

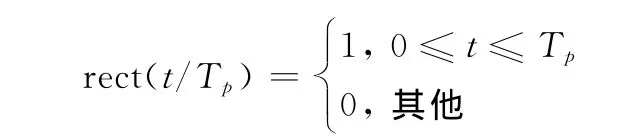
Tp为脉冲宽度；Tr为脉冲重复周期；fc为信号载频；K为调频率（K＞0）；φ为随机初相；Np为发射脉冲数。

沿径向直线运动的目标在时刻t与雷达相距R（t），若回波能量无损失，则根据式（1）可得第m个脉冲回波经混频后为

式中，p（t）＝rect（t／Tp）exp（jπKt2）；c为光速；λc为波长；为快时间；tm＝（m－1）Tr为慢时间。

由式（2）可得回波快时间维的离散频谱为

式中，fs为采样率；fk＝kfs／Ns，k＝0，1，…，Ns，Ns＝fsTr；P（f）为p（t）的频谱，可由驻定相位原理求得且｜P（fk）｜＝

若目标具有L阶运动参数（L≥2），其运动方程可表示为

记

若存在xn≥0，yn≤0满足

则R（n）（0）的分辨率即定义为Δn＝xn－yn。

当Tr较小时

根据定积分的相关知识，求解满足式（5）的xn可先转化为求解满足，进而可得，同理可求得（y′＜0）。由xn和yn的表达式可以发现，同一运动参数在不同的fk下对应不同的分辨率，但对于窄带信号，fk对分辨率的影响可以忽略。

当n＞1时，无法得到解析的y′，只能通过数值求解，表1列出通过数值求解得到的各阶运动参数的分辨率。

表1 各阶运动参数的分辨率

若在积累时间内某阶运动参数的变化不大于相应分辨单元，则可近似认为该阶参数对相参积累的影响可以忽略，反之则需在运动模型考虑该阶参数。

2 基于MNUFFT的相参积累算法

若记

则式（3）可简化表示为

令

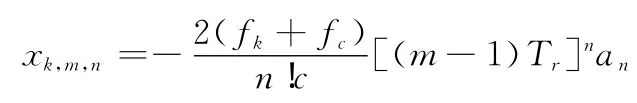
其中，an为R（n）（0）可能取到的最大值，则对式（8）完成相位补偿并沿慢时间维进行累加可得

式中，ln＝0，1，…，Nln；an／Nln与R（n）（0）的理论分辨率相等。

根据文献［15］可得

式中

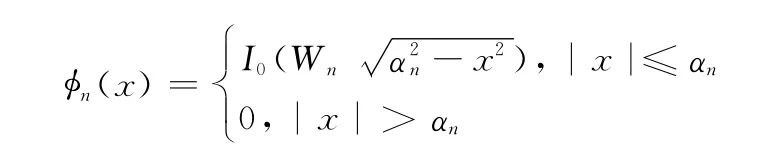
I0（x）为第一类零阶修正贝塞尔函数；un为大于1的常数，本文均取1．1；Wn为大于1的正整数，本文均取2；αn略小于π（2－1／un），本文均取π（2－1／un）－0．01；ln＝－Nln／2～Nln／2－1（n＝1，2，…，L）。

将式（10）代入式（9）通过推导可得

其中

以上利用MNUFFT实现相位补偿的过程主要分为3步：

步骤1 通过扩展长度的插值由一维向量［Sr（fk，t1），Sr（fk，t2），…，Sr（fk，tNp）］T得到L维矩阵U；

步骤2 计算矩阵U的L维FFT；

记

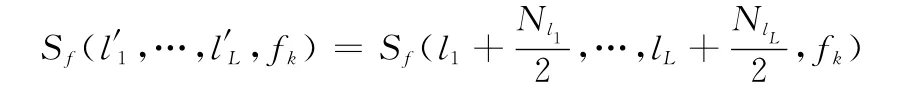
则经过对Sf（l′1，…，l′L，fk）作IFFT转换到快时间域从而最终实现对具有高阶运动特性的目标的相参积累。

若｜Sf（l′1，…，l′L，n）｜超过检测门限，则可以根据相应l′1，…，l′L，n的数值得到各阶参数的估计值

3 基于WNUFFT的相参积累算法

参照z（n）的离散Wigner－Ville分布的形式将z（n）的WNUFFT定义为

式中，Xm为m的任意函数。

当目标最高阶的运动参数为加加速度时，根据式（8）可得第m个脉冲回波的快时间频谱为

在慢时间维，对Sr（fk，tm）的前Np／2和后Np／2项分别作WNUFFT，可得

其中

式（17）和式（18）可通过一维NUFFT计算得到，且可知l＝（NpTrR（3）（0）／4＋R（2）（0））／Δa2时，｜Wfk（Np／4＋1，l）｜取得最大值；l＝（3 NpTrR（3）（0）／4＋R（2）（0））／Δa2时，｜Wfk（3 Np／4＋1，l）｜取得最大值。

若记｜Wfk（Np／4＋1，l）｜最大值点对应的l为l1，｜Wfk（3 Np／4＋1，l）｜最大值点对应的l为l2，那么可以求得加速度和加加速度的估计值分别为

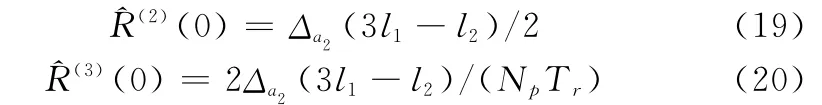
为尽量保证在高信噪比下对l1和l2进行估计，需将Wfk（Np／4＋1，l）和Wfk（3 Np／4＋1，l）通过IFFT变换到快时间域，进而搜索到峰值点对应的位置，得到l1和l2。

根据估计的加速度和加加速度值即可补偿式（14）中的二次项和三次项，从而得到

此时S′r（fk，tm）可看作匀速运动目标的快时间频谱，令为速度搜索间隔，一般设为不大于速度分辨率的数值，对S′r（fk，tm）进行NUFFT，可得

在快时间频域完成速度、加速度和加加速度的补偿后，对Sf（l，fk）作IFFT转换到快时间域，即完成相参积累，并可根据输出模值峰值点位置得到初始距离和初始速度的估计值。

基于WNUFFT的长时间相参积累算法的实现流程如图1所示。

图1 基于WNUFFT的相参积累算法实现流程图

4 仿真结果与分析

由于本文的研究背景是基于某米波全向雷达，故基本仿真参数设置如下：载频150MHz，带宽5MHz，脉冲宽度50μs，调频率2×1010Hz／s，脉冲重复周期1ms，接收脉冲个数1 000，时域采样率5MHz。

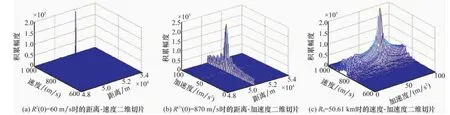
图2 匀加速运动目标积累结果

假设目标沿径向朝雷达匀加速运动，初始速度840m／s，加速度60m／s2，初始距离51．029km，则参考速度R（1）（0）为870m／s，参考距离R0为50．61km。当加速度搜索的最大值100m／s2，搜索间隔数50时，在无噪声的情况下利用MNUFFT实现相参积累的结果如图2所示。

综合图2（a）～图2（c）可知，积累最大值出现在R0＝50．61km，R（1）（0）＝870m／s，R（2）（0）＝60m／s2处，与期望的数值一致，说明利用MNUFFT可以有效补偿高阶相位项，从而实现相参积累。

GRFT作为RFT的多维推广，可直接在时域实现高阶运动目标的长时间相参积累。在频域，通过遍历搜索并完成高次相位项的补偿后，可利用Keystone变换或Chirp Z变换补偿剩余的一次相位项，从而完成所有相位项的补偿，以便最终完成积累。

在高斯白噪声背景下，分别利用MNUFFT、Chirp Z变换、Keystone变换和GRFT对匀加速运动目标进行相参积累后的检测性能曲线如图3所示，其中虚警概率为10－6。

图3 高阶运动目标相参积累算法检测性能对比

由图3可知，若要求检测概率为0．9，则MNUFFT、Chirp Z变换、Keystone变换和GRFT对应的脉冲压缩后信噪比与理论值分别相差0．2dB，0．2dB，1．8dB，4．7dB。这说明基于MNUFFT的相参积累算法在积累性能上与Chirp Z变换相同，而优于Keystone变换和GRFT。

选用何种积累算法除了考虑其积累性能，实现的计算复杂亦是一项重要依据。假设速度以及各阶加速度的搜索间隔等于各自的分辨率，距离的搜索间隔为c／（2fs），目标速度不超过nb倍盲速。由于各阶加速度在实际中出现模糊的可能性远小于速度，故仅考虑盲速。记k阶加速度的搜索间隔数为Nak（k＝1，2，…，La，La＝L－1）。

实现基于GRFT、Keystone变换、Chirp Z变换和MNUFFT的相参积累算法所需的复乘和复加次数如表2所示。

表2 高阶运动目标相参积累算法实现计算复杂度对比

由表1知，波长为2m，积累1s时，加速度的分辨率为7m／s2，加加速度的分辨率为36m／s3，更高阶的加速度因分辨率更低而实际考虑得并不多，因此在计算量的数值对比中只考虑到加加速度。当Na1＝Na2＝20时，则搜索的加速度和加加速度的最大值分别为140m／s2和720m／s3，能满足一般应用场景，同时取Ns＝5 000，则实现基于GRFT、Chirp Z变换、Keystone变换和MNUFFT的相参积累需要的复乘次数随积累脉冲数Np和速度模糊数nb的变化分别如图4和图5所示。

由图4（a）知，基于GRFT和Keystone变换的相参积累算法计算复杂度高于基于Chirp Z变换和MNUFFT的相参积累算法，且随着脉冲积累数的增加，基于GRFT和Keystone变换的相参积累算法的相对计算复杂度越来越高。由图4（b）知，nb＝1时，基于Chirp Z变换的相参积累算法相对于基于MNUFFT的相参积累算法，其计算复杂度随着脉冲积累数的增加亦越来越高，但不会高于后者的2倍，当积累脉冲数为1 000时，实现基于MNUFFT的相参积累算法所需复乘次数约为基于Chirp Z变换的算法的60%。

由图5（a）知，基于GRFT、Keystone变换和Chirp Z变换的相参积累算法相对于基于MNUFFT的相参积累算法，计算复杂度随速度模糊数的变化不大。由图5（b）知，随着速度模糊数的增大，基于MNUFFT的相参积累算法相对于基于Chirp Z变换的相参积累算法在计算复杂度上的优势越来越小。

综上所述，若目标速度小于1倍盲速，利用多维NUFFT实现相参积累的计算复杂度相对其他算法的优势最大；若目标速度大于1倍盲速，建议按照常规思路先通过各阶加速度的搜索完成高阶相位项的补偿，而后利用NUFFT完成一次相位项的补偿，这样可以保证其相对已有算法在计算复杂度上的优势。而对于米波雷达，若合理选择载频和脉冲重复频率，使飞机和一般导弹类目标在1倍盲速内是可能的。

图4 实现相参积累所需复乘次数随Np的变化曲线

图5 实现相参积累所需复乘次数随nb的变化曲线

下面验证基于WNUFFT的长时间相参积累算法的有效性。

假设某运动目标初始速度840m／s，初始加速度60m／s2，加加速度72m／s3，初始距离51．029km。当脉压前信噪比为－5dB，加速度搜索间隔为2m／s2时，在快时间频域沿慢时间维进行两次WNUFFT后转换到快时间域的结果分别如图6和图7所示。

图6 前Np／2点WNUFFT后IFFT的结果

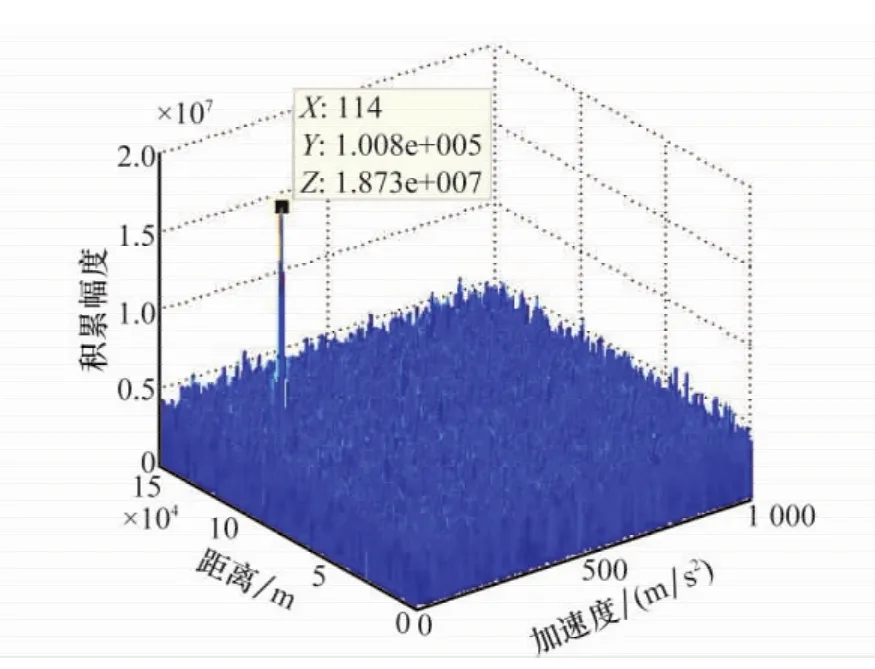
图7 后Np／2点WNUFFT后IFFT的结果

由图6知，对前Np／2点作WNUFFT再经IFFT转换到快时间域的输出幅度峰值点对应的加速度数值为78m／s2，故有＾R（2）（0）＋＾R（3）（0）NpTr／4＝78m／s2；由图7知，对后Np／2点作WNUFFT再经IFFT转换到快时间域的输出幅度峰值点对应的加速度数值为114m／s2，故有＾R（2）（0）＋3＾R（3）（0）NpTr／4＝114m／s2，从而可以得到加速度和加加速度的估计值分别为60m／s2和72m／s3。

利用得到的加速度和加加速度估计值对快时间频谱的二次和三次相位项进行补偿，而后沿慢时间进行NUFFT，并转换到快时间域完成积累，其积累结果如图8所示。

图8 完成运动补偿后积累结果

由图8知，积累峰值出现在（51．03km，840m／s）处，与设定的运动参数数值相符，说明实现了有效的积累。

然而，能否达到如图8所示的理想积累效果，取决于能否实现对初始加速度和初始加加速度的高精度估计，而利用WNUFFT实现对加速度和加加速度的准确估计对回波信号的信噪比提出了较高要求，因此基于WNUFFT的相参积累算法更适用于回波信噪比较高的情况。

记实现基于WNUFFT和MNUFFT的相参积累算法所需复乘次数分别为CWNT和CMNT。为便于比较，假定Na1＝Na2＝20，Ns＝5 000，则当nb＝1时，CMNT／CWNT随Np的变化如图9所示；当Np＝1 000时，CMNT／CWNT随nb的变化如图10所示。

图9 CMNT／CWNT随Np的变化曲线

图10 CMNT／CWNT随nb的变化曲线

由图9和图10知，随着脉冲积累数和速度模糊数的增大，CMNT／CWNT趋于某定值，说明基于WNUFFT的积累算法在计算复杂度上的优势在一定范围内的增加后将保持不变，但CWNT仍然比CMNT低2个数量级。

因此，相对于基于MNUFFT的相参积累算法，基于WNUFFT的相参积累算法极大地降低了计算复杂度，但其对回波脉压前信噪比亦有相对更高的要求。

5 结 论

本文针对高阶运动目标的相参积累问题，提出了在快时间频域沿慢时间维利用多维NUFFT进行运动补偿后利用IFFT转换回快时间域的方法，相对于已有积累算法，在目标速度不超过1倍盲速时，该方法既不存在积累损失且计算量至少减少40%。特别地，针对具有加加速的目标，进一步提出了基于Wigner－NUFFT的相参积累算法，该算法相对基于MNUFFT算法计算量极大地减小，但对其积累前单个脉冲的信噪比的要求更高。

［1］Li P，Zhou H F，Zhang B．A study on long－term integration based on segmented range［J］．Modern Radar，2012，34（7）：20－24．（李品，周海峰，张飙．基于距离分段的目标长时间积累方法研究［J］．现代雷达，2012，34（7）：20－24．）

［2］Zhang S S，Zeng T，Long T，et al．Dim target detection based on Keystone transform［C］∥Proc．of the IEEE International Radar Conference，2005：889－894．

［3］Bao Q L，Chen Z P，Zhang Y，et．al．Long term integration of radar signals with unknown Doppler shift for ubiquitous radar［J］．Journal of Systems Engineering and Electronics，2011，22（2）：219－227．

［4］Tian C，Wen S L．A long－term coherent integration algorithm based on non－uniform fast Fourier transform［J］．Journal of Electronics ＆Information Technology，2014，36（6）：1374－1379．（田超，文树梁．基于非均匀FFT的长时间相参积累算法［J］．电子与信息学报，2014，36（6）：1374－1379．）

［5］Carlson B D，Evans E D，Wilson S L．Search radar detection and track with the Hough transform（I）：system concept［J］．IEEE Trans．on Aerospace and Electronic Systems，1994，30（1）：102－108．

［6］Carlson B D，Evans E D，Wilson S L．Search radar detection and track with the Hough transform（Ⅱ）：detection statistics［J］．IEEE Trans．on Aerospace and Electronic Systems，1994，30（1）：109－115．

［7］Carlson B D，Evans E D，Wilson S L．Search radar detection and track with the Hough transform（III）：detection performance with binary integration［J］．IEEE Trans．on Aerospace and Electronic Systems，1994，30（1）：116－125．

［8］Sun Y，Willett P．Hough transform for long chirp detection［J］．IEEE Trans．on Aerospace and Electronic Systems，2002，38（2）：553－569．

［9］Wu Z P，Wu H Y，Su T．Integration of target energy in 3－D radar data of range－Doppler－time［J］．Systems Engineering andElectronics，2013，35（1）：68－72．（吴兆平，吴惠阳，苏涛．距离－多普勒－时间三维雷达数据中的目标能量积累［J］．系统工程与电子技术，2013，35（1）：68－72．）

［10］Xu J，Yu J，Peng Y N．Radon－Fourier transform for radar target detection（I）：generalized Doppler filter bank［J］．IEEE Trans．on Aerospace and Electronic Systems，2011，47（2）：1186－1202．

［11］Zeng J K，He Z S，Mahtini S，et al．Modified Hough transform for searching radar detection［J］．IEEE Geoscience and Remote Sensing Letters，2008，5（4）：683－686．

［12］Kirkland D．Imaging moving targets using the second－order Keystone transform［J］．IET Radar Sonar ＆Navigation，2011，5（8）：902－910．

［13］Yu J，Xu J，Peng Y N．Long time coherent integration method for targets with a radial acceleration［J］．Journal of Tsinghua University（Science ＆Technology），2010，50（5）：793－796．（余吉，许稼，彭应宁．径向匀加速目标的长时间相参积累方法［J］．清华大学学报（自然科学版），2010，50（5）：793－796．）

［14］Yu J，Xu J，Peng Y N．Radon－Fourier transform for radar target detection（III）：optimality and fast implementations［J］．IEEE Trans．on Aerospace and Electronic Systems，2012，48（2）：991－1004．

［15］Karsten F．Non－equispaced fast Fourier transform with applications to tomography［J］．The Journal of Fourier Analysis and Application，2003，9（5）：431－450．

E－mail：qctchao87＠126．com

文树梁（1971－），男，研究员，博士，主要研究方向为雷达系统和雷达信号处理。

E－mail：wenshul＠sina．com

杜智远（1976－），男，高级工程师，硕士，主要研究方向为测控总体技术。

E－mail：51077993＠qq．com

Long time coherent integration algorithm for moving targets with high order motion

TIAN Chao1，WEN Shu－liang1，DU Zhi－yuan2
（1．Beijing Institute of Radio Measurement，Beijing 100854，China；2．Unit 92493of the PLA，Huludao 125001，China）

A long time coherent integration algorithm based on multi－dimensional non－uniform fast Fourier transform（NUFFT）is proposed for moving targets with arbitrary orders of motion．The presented algorithm firstly utilizes multi－dimensional NUFFT to realize motion compensation in the fast－time frequency domain，and then accomplishes coherent integration via inverse fast Fourier transform（IFFT）．The performance of this algorithm is almost optimal while the computational complexity is less than that of the existed algorithms．Especially，another new algorithm with Wigner－NUFFT is used to deal with a target with a jerk．Compared to the algorithm with multi－dimensional NUFFT，the algorithm with Wigner－NUFFT has much lower computational complexity．However，the disadvantage is that a higher signal－to－noise ratio is needed．The simulation results demonstrate the effectiveness of the proposed algorithm．

coherent integration；non－uniform fast Fourier transform（NUFFT）；high order motion；motion compensation

TN 95

A

10．3969／j．issn．1001－506X．2015．06．01

田 超（1987－），男，博士研究生，主要研究方向为雷达总体技术。

1001－506X（2015）06－1229－08

2014－09－12；

2014－11－16；网络优先出版日期：2014－12－12。

网络优先出版地址：http：／／www．cnki．net／kcms／detail／11．2422．TN．20141212．0901．004．html