Adaptive Sliding Mode Control for Re-entry Attitude of Near Space Hypersonic Vehicle Based on Backstepping Design
Jingmei Zhang,Changyin Sun,Ruimin Zhang,and Chengshan Qian
Adaptive Sliding Mode Control for Re-entry Attitude of Near Space Hypersonic Vehicle Based on Backstepping Design
Jingmei Zhang,Changyin Sun,Ruimin Zhang,and Chengshan Qian
—Combining sliding mode controlmethod with radial basis function neural network(RBFNN),this paper proposes a robust adaptive control scheme based on backstepping design for re-entry attitude tracking controlofnear space hypersonic vehicle (NSHV)in the presence of parameter variations and external disturbances.In the attitude angle loop,a robust adaptive virtual controllaw is designed by using the adaptive method to estimate the unknown upper bound of the compound uncertainties.In the angular velocity loop,an adaptive sliding mode control law is designed to suppress the effect of parameter variations and external disturbances.The main benefit of the sliding mode controlis robustness to parameter variations and externaldisturbances.To further improve the control performance,RBFNNs are introduced to approximate the compound uncertainties in the attitude angle loop and angular velocity loop,respectively.Based on Lyapunov stability theory,the tracking errors are shown to be asymptotically stable.Simulation results show that the proposed control system attains a satisfied control performance and is robust against parameter variations and external disturbances.
Index Terms—Hypersonic vehicle,attitude control,backstepping design,sliding mode control radial basis function neural network(RBFNN).
I.INTRODUCTION
D URING the hypersonic re-entry ofnearspace hypersonic vehicle(NSHV),the vehicle suffers complex flight environment,the wide range of speed,the high flight altitude, and the tremendous changes of gas thermal properties and aerodynamic characteristics.Therefore,the NSHV is a complex nonlinear system with many uncertainties,and the control system design is very challenging[1−4].Different nonlinear control methods have been proposed to design flight control system for the NSHV under severe uncertainties,such as sliding mode control[5−8],fuzzy control[8−9],and predictive control[10−11].
Backstepping control[12]is an effective design method for nonlinear uncertain systems,whether the system uncertainties satisfy the matched condition or not.It shows unique advantages in dealing with nonlinear system problems.By selecting a suitable Lyapunov function,one can construct virtual control laws step by step,such that a stable control system is obtained.Moreover,the global stability of closedloop system can be guaranteed.However,a disadvantage of the traditionaladaptive backstepping design method is thatthe system should be parameterized[13−15].
Sliding mode control[16−17]is another effective method for nonlinearcontrolsystem.The sliding mode controlis designed to drive and confine the system states to stay in the prescribed sliding surface which exhibits the desired dynamics.In the sliding mode,the closed-loop system becomes insensitive to the plant parameter variations and external disturbances.
Zhou etal.[17]proposed a robustbackstepping sliding mode controlmethod for nonlinear systems to suppress the influence of uncertainties.However,the sliding mode controller was designed based on the upper bounds of the uncertainties.It required thatthe upper bounds were known in advance.In[18], by combining the backstepping control,adaptive control,and sliding mode control,a new adaptive backstepping controller was proposed.Note that in[18],the derivation of virtual control was treated as an uncertainty,which brought conservatism to design the controller.Plestan et al.[19]proposed a new adaptive sliding mode controlmethod,where the adaptive gains were adjusted in a new manner,which ensured thatthere was no over-estimation of the gains with respectto the real a prioriunknown value of uncertainties.Moreover,the proposed method guaranteed the system dynamics arrived at the sliding mode surface within a finite time.
Radial basis function neural network(RBFNN)has been proved to own the superior ability to approximate nonlinear continuous function with arbitrary precision[20].Moreover,it has less computational burden,simpler network structure,and faster convergence than a multilayer perceptron since only the connective weights between the hidden layer and the output layer of the network are adjusted during training.Therefore, the RBFNN is very useful for applications in the control of nonlinear systems[21−22].For example,based on RBFNN,a robustcontrol design method was proposed for strict-feedback block nonlinear systems with mismatched uncertainties[23].
Motivated by the discussion mentioned above,this paper proposes a robustcontrolmethod forthe attitude controlofthe NSHV.The proposed controlmethod combines the advantages of the adaptive sliding mode control method,RBFNN and backstepping.Firstly,the attitude controlmodelof the NSHVand an assumption are introduced.Then an adaptive backstepping control approach is proposed.In the attitude angle loop,an adaptive control term is designed to suppress the effect of the compound uncertainties.In the angular rate loop,an adaptive sliding mode control is integrated into the backstepping design.The adaptive gains of sliding mode control are dynamically tuned based on the constructed gain dynamics,which can ensure that there is no over-estimation of the controlgains.The stability of the proposed approach is analyzed using the Lyapunov method.To improve the control performance and increase the robustness of the backstepping control system,the RBFNNs are introduced to estimate the uncertainties in the attitude angle and angular rate loops, respectively.Thus the robust adaptive control approach not only owns a strong robustness againstparametervariations and external disturbances,but also can efficiently save the control efforts.And the stability of the closed-loop system is proved based on the Lyapunov stability theory.Finally,the simulation results show that the proposed approach attains a satisfactory performance in the presence of parameter variations and external disturbances.
II.PROBLEM DESCRIPTION
The considered attitude control model of the NSHV comes from the hypersonic vehicle of winged-cone configuration[24−25].The equations with 6 degrees of freedom and 12 states can be simplified into the affine nonlinear equations as

where x1=[α,β,µ]Tis the attitude angle vector,x2= [p,q,r]Tis the attitude angular rate vector,u=gfδδ+Mris the control input,fs,ff∈R3are nonlinear vector functions, Gs1,Gf∈R3×3are the invertible matrices.The concrete expressions of matrices above are specified in[21].Φ1,Φ2are compound uncertainties,which contain parameter variations and external disturbances.
Assumption 1.The uncertainties of the NSHV satisfy‖Φi‖≤ϕi,whereϕiis an unknown constant,i=1,2.
The main purpose of this paper is to design a robust adaptive virtual control law x2dand a control law u based on backstepping method,such that the re-entry attitude of the NSHV x1can track the given target x1dasymptotically.
III.THE ROBUST ADAPTIVE SLIDING MODE CONTROL DESIGN
Step 1.Design the virtual control law to suppress the influence of uncertainty in attitude angle loop(1).
Define the error state vector as

From(1)and(3),one can obtain

Then a virtual control law is designed as
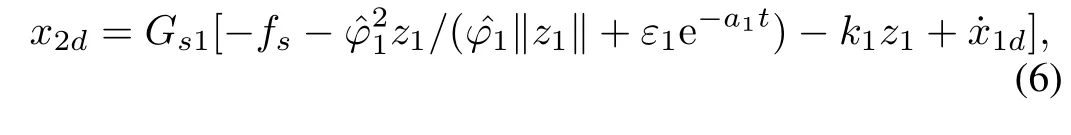
whereε1>0,a1>0.ˆϕ1is the estimated value ofϕ1and the adaptive law is shown as

Consider the following Lyapunov function:

Differentiating V1with respect to time and using(6),one can obtain

If the tracking error z2converges to zero,z1is asymptotically stable under the effect of virtual control(6).
Step 2.Design the actual control variable u to make the tracking error of angular velocity loop z2converge to zero.
In order to well dispel parameter variations and external disturbances,sliding mode control is employed to design the actualcontrollaw,such thatthe system dynamics arrives atthe sliding mode surface within a finite time.At the same time, in order to avoid the gain of the sliding mode becomes too large,this paper introduces an adaptive control law to adjust the gain of the sliding control.
According to(2)and(4),the error equation is given as

The sliding mode surface is shown as follows:
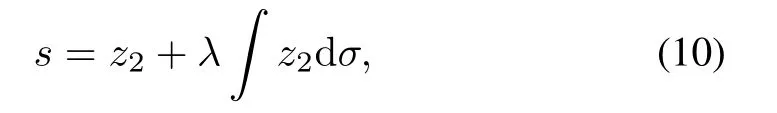
whereλ > 0 decides the bandwidth of the error state s=[s1,s2,s3]T.
The control law u can be designed as follows:
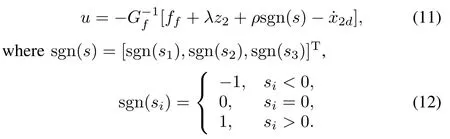
The gain of controlρ(t)∈R is selected as follows:
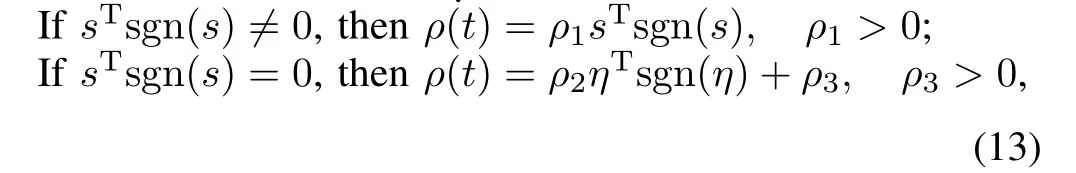
whereρ2=ρ(t∗),τ˙η+η=sgn(s),τ>0.t∗is the arrival time,such that s=0 at t=t∗.
For the firstcase sTsgn(s)/=0 in(13),a Lyapunov function candidate is chosen as

whereρ∗>0 is the upper bound ofρ,andγ2>0.The time derivative of(14)is shown as follows:

Substituting the control law(11)into the above equation yields

From Assumption 1 and(15),one can obtain

From Lemma 1 in[19],there existsρ∗> 0 such that ρ(t)≤ ρ∗for all t> 0,and thus(16)can be represented as
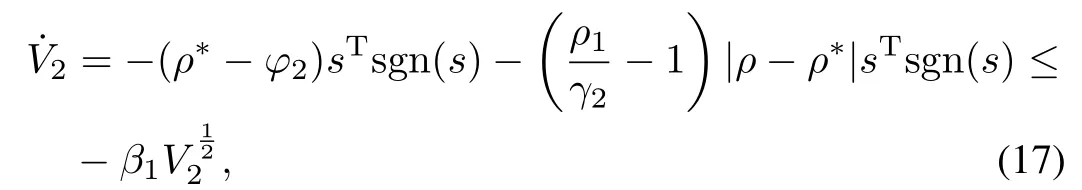

Formulation(17)shows that there exists a finite time such that s=0 for all t≥ tF.Thus,the proposed controllaw(11)and the adaptive gain given by(13) satisfy the sliding condition.
Next,let us consider the case of sTsgn(s)=0.According to Theorem 1 in[19],the control law(11)with the updated law(13)can ensure that the states of system(9)stay on the sliding surface s=0.
Based on the above analysis,we can obtain the following theorem.
Theorem 1.Considerthe closed-loop nonlinear systems(1) and(2),where the virtual control law x2dis given by(6),and the control input u is defined by(11)with the control gain of (13)and the parameter adaptive law of(7).The trajectories of the system are globally exponentially convergent,and the sliding surface s=0 is reachable.Meanwhile,the re-entry attitude state x1=[α,β,µ]Tof the NSHV asymptotically tracks the given target x1d=[αc,βc,µc]T.
Remark 1.Because the sign function sgn(·)may bring the chattering problem,the saturation function[26]sat(si/σi)is adopted in this paperto replace the sign function sgn(·),which is
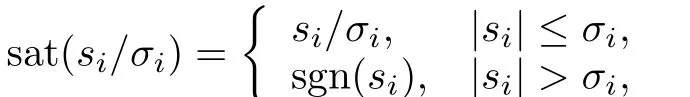
whereσi>0 is a boundary layer thickness.
IV.ADAPTIVE BACKSTEPPING SLIDING MODE CONTROL DESIGN BASED ON RBFNN
Compared to the traditional sliding mode controller,the sliding mode controller with the designed adaptive gain do not need the prior knowledge of the upper bounds of the compound uncertainties in the preceding section.So it can provide robustness in the presence of parameter variations and external disturbances.However,when the uncertainties are increased,the gains are required to increase for achieving robustness,and control chattering is aggravated.In fact,the controlgain cannotbe arbitrarily large value because ofcontrol input limitation of the NSHV.To deal with this problem,the sliding mode controller with adaptive gain is combined with neural networks to compensate for the effects of uncertainties.
RBFNN has been widely used for approximating nonlinear functions due to its structuralsimplicity.Itcomprises an input layer,a hidden layer and an output layer,which is shown in Fig.1.

Fig.1.The structure of RBFNN.
Given an input x∈Rn,the output of the RBFNN can be represented as

where W=[wij]N×mis weight matrix which connects the hidden layer to the output layer,N and m are the numbers of neurons in the hidden layer and network output dimension, respectively.φ=[φ1,···,φN]T.The Gaussian basis function φiis chosen as

whereξ=[ξT1,···,ξTN]Tis the center vector of the Gaussian basis function,andηis the width of the Gaussian basis function.
Itshould be noted thatthe weights and center values of the RBFNN have significant effects on approximation precision, while the influence of the width is little.In order to reduce computational burden,we choose the width value as constant in this paper.It has been proved that the RBFNN can approximate a bounded continuous function f(x)with arbitrary precision on the compact setin[21].So

whereδf(x)denotes the approximation error,W∗,ξ∗denote the optimal weights and center values,respectively.
Similar to the analysis of the preceding section,the design of control system is given based on backstepping method.
Step 1.Design the virtual control law to suppress the influence of the uncertainty in the attitude angle loop(1).
For the error dynamics(5)of the angular loop,we design the virtual control law as
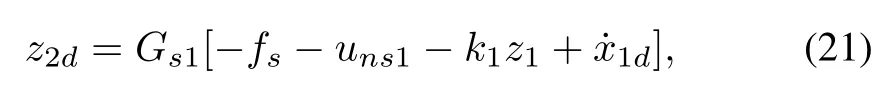
where uns1=unn1+us1,unn1is the estimation ofuncertainty Φ1,which is

and W1,ξ1are computed by the following adaptive laws, respectively:

whereζ11,ζ12are learning rates.
Moreover,to confront the approximation errorδ1=Φ1−unn1,an adaptive robust term is adopted,i.e.,

whereˆδ1is the estimated value ofδ1and the adaptive law is shown as
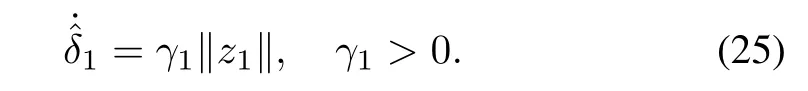
For convenience,we will rewriteΦ1as

The Taylor series expansion ofφ(z1,ξ∗1)in(19)atξ1can be represented as


According to the property of RBFNN,‖o(z1,˜ξ1)‖is bounded.Then the RBFNN approximation errorΦ1is as follows:

Consider the following Lyapunov function:

where˜W1=W∗1−W1,˜ξ1=ξ∗1−ξ1,˜δ1= ˆδ1−δ1,and ˙˜W1= − ˙W1,˙˜ξ1= −˙ξ1,˙˜δ1= −˙δ1.The time derivative of (30)is shown as follows:
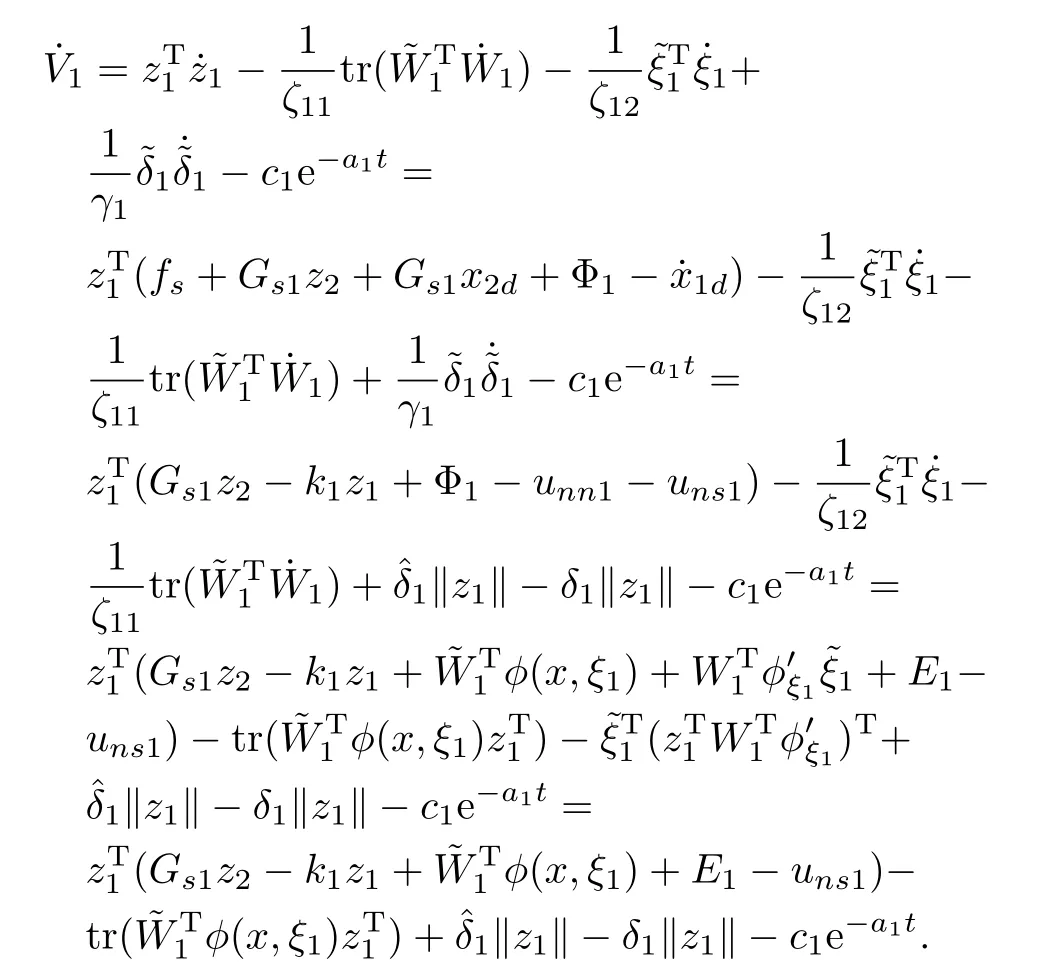
It is known that zT1˜WT1φ(x,ξ1)=tr(˜WT1φ(x,ξ1)zT1)and

So it can be referred that

Therefore,if the tracking error z2of angular velocity loop converges to zero,z1is asymptotically stable under the effect ofvirtualcontrol(21).In otherwords,state x1tracks the target signal x1dasymptotically.
Step 2.Design the actual control variable u to make the tracking error of angular velocity loop z2converge to zero. From(2)and(21),one can obtain the error dynamic equation

The sliding mode surface is chosen the same as(10).Then, the control law u can be designed as follows:

where sgn(s)is given by(12),andρ(t)∈R is calculated by (13).unn2is adopted to estimate the uncertaintyΦ2,and has the following expression:
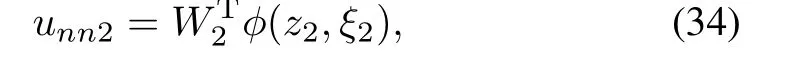
where W2,ξ2are computed by the following adaptive laws:
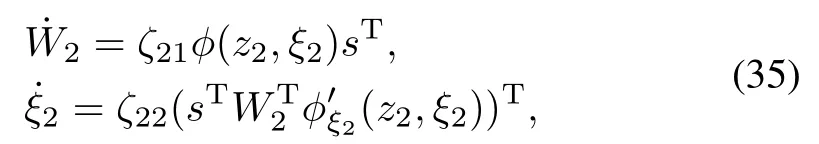
whereζ21>0,ζ22>0 are learning rates.Φ2can be rewritten as
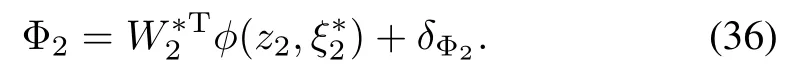
And E2=δ2>0.
Theorem 2.Consider the closed-loop nonlinear system equations(1)and(2),where the virtual control law x2dis given by(21)and the control input u is defined by(33)with the control gain of(13)and the parameter adaptive laws of (23),(25)and(35).The trajectories of the system are globally exponentially convergent,and the sliding surface s=0 is reachable.Meanwhile,the re-entry attitude state x1of the NSHV asymptotically tracks the given target x1d.
Proof.The proof consists of two cases;the first case is sTsgn(s)/=0 and the second is sTsgn(s)=0.
First,let us consider the first case(sTsgn(s)/=0).The following Lyapunov function candidate is considered:

Inequality(39)shows that there exists a finite time tF≤such that s=0 for all t>tF.Thus,the proposed control law(33)and the adaptive gain given by(13)satisfy the sliding condition.
Next,let us consider the case of sTsgn(s)=0.According to Theorem 1 in[19],the control law(33)with the adaptive laws(13)and(35)can guarantee the states of system(9)stay on the sliding surface s=0.
In summary,itcan be concluded thatthe trajectories of the system are globally exponentially convergent,and the sliding surface s=0 is reachable.Meanwhile,the re-entry attitude state x1of the NSHV can welltrack the given command x1d.□
Remark 2.Itis hard to calculate˙x2d=[˙x2d1,˙x2d2,˙x2d3]T. So the robust differentiator[27]is introduced to handle this problem,which is

whereλ1i> 0,λ0i> 0.Levant[27]proved that the robust differentiatorcan estimate the first-orderderivative ofthe input signal exactly if there is no noise in the input.That is to say, z0i=αi,z1i= ˙αiare obtained within a finite time.When there is some noise in the input,the estimate error can be offset by the robustness terms.
V.SIMULATIONS
The initial conditions of simulation are V0=3.1 km/s, H0=34 km,α0=1°,β0=0.2°,µ0=−1°,p0=q0= r0=0°/s.The command signals areαc=−1°,βc=0°, µc=1°given by the command filter 2/(s+2).Suppose there exist uncertainties in the aerodynamic parameter.Besides, the disturbance torque in angular velocity loop is defined as 105×[sin(t),cos(2t),sin(3t)]TN·m.
The parameters of the control system are given by k1= diag{0.8,0.8,0.8},λ=diag{1.2,1.2,1.2},a1=2,ε1=0.5, ρ1=2,ρ2=0.5,ρ3=0.2,τ=0.1,σi=0.02,ζ11=2, ζ12=1,ζ21=1,ζ22=0.5.The number of hidden layer neurons in the RBFNN is 4.
For comparative simulation,the traditional backstepping method is also employed to design the attitude control system for the NSHV as follows:

The parameters of the control system(41)~(42)are k1= diag{5,5,5},k2=diag{10,10,10}.The simulation results are shown in Figs.2 and 3,where subscript c means command signal,subscripts 1,2 express the simulation result of the traditional backstepping control method and the method proposed in this paper,respectively.Fig.2 shows the changing curve of attitude angle and angular rate.It is observed thatthe performance of the proposed control method is much better than thatof the traditionalbackstepping controlmethod.Fig.3 shows that large rudder surface deflections occur when using the traditional backstepping control method,it is because a high controlgain is necessary to suppress parameter variations and external disturbances.In contrast,the proposed method avoids this problem.

Fig.2.Comparison of attitude control performance.
VI.CONCLUSION
In this paper,a strongly robustadaptive sliding mode control system is proposed based on backstepping design,the adaptive control technique and the RBFNN for the attitude tracking problem of the NSHV in the presence of parameter variations and external disturbances.Firstly,to relax the requirement for the upper bound of the compound uncertainty in control design,an adaptive control technique is employed.Based on backstepping design,in attitude angular loop,the unknown upper bound is estimated by using an adaptive term,and then a virtual control law is derived.In angular rate loop,sliding mode control with the adaptive gain is considered to design the real control law.Moreover,the constructed gain dynamics can ensure that there is no over-estimation of the control gain.Secondly,to furtherimprove the controlperformance,the RBFNN is employed to estimate the compound uncertainties directly.Moreover,an adaptive control term designed in the firststep are used to dealwith the approximated errors.Thus, based on the similar design in the firststep,the virtualcontrol law in the attitude angular loop and the real control law in the angular rate loop are obtained,respectively.Furthermore, the closed-loop stability is proved using Lyapunov theorem.Finally,simulation results show good performance of the proposed control approach for the NSHV attitude control. Moreover,the robustness to parameter variations and external disturbances are successfully accomplished.
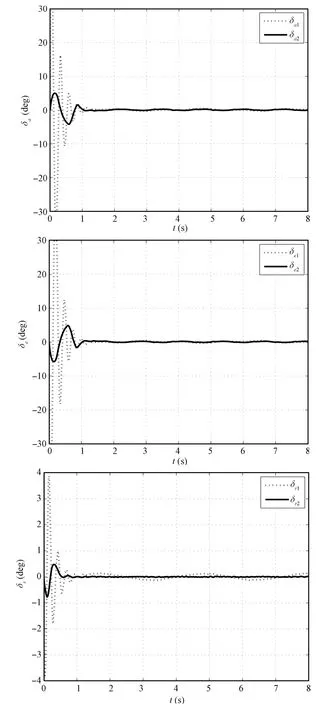
Fig.3 Comparison of control surface deflections
REFERENCES
[1]He Jie,Zheng De-Zhai.Characteristics and key technology research for hypersonic vehicle.In:Proceedings of the 2012 Aerospace Science and Technology Innovation and the Yangtze River Delta Economic Transformation Development BBS.Lianyungang,China:2012.227−231(in Chinese)
[2]Chen Zong-Ji,Zhang Ru-Lin,Zhang Ping,Zhou Rui.Flight control, challenges and opportunities.Acta Automatica Sinica,2013,39(6): 703−710(in Chinese)
[3]Bao Wei-Min.Presentsituation and development tendency of aerospace control techniques.Acta Automatica Sinica,2013,39(6):697−702(in Chinese)
[4]Sun Chang-Yin,Mu Chao-Xu,Yu Yao.Some control problems for near space hypersonic vehicles.Acta Automatica Sinica,2013,39(11): 1901−1913(in Chinese)
[5]Xu H J,Mirmirani M D,Ioannou P A.Adaptive sliding mode control design for a hypersonic flightvehicle.Journalof Guidance,Control,and Dynamics,2004,27(5):829−838
[6]Zhang R M,Sun C Y,Zhang J M,Zhou Y J.Second order terminal sliding mode controlforhypersonic vehicle in cruising flightwith sliding mode disturbance observer.Journal of Control Theoryand Applications, 2013,11(2):299−305
[7]Zhang R M,Wang L,Zhou Y L.On-line RNN compensated second order nonsingular terminal sliding mode control for hypersonic vehicle. International Journal of Intelligent Computing and Cybernetics,2012, 5(2):186−205
[8]Li Jing-Jing,Ren Zhang,Song Jian-Shuang.Fuzzy sliding mode control forhypersonic re-entry vehicle.JournalofShanghaiJiaotongUniversity, 2011,45(2):295−300(in Chinese)
[9]Da Costa R R,Chu Q P,Mulder J A.Reentry flight controller design using nonlinear dynamic inversion.Journal of Spacecraft and Rockets, 2003,40(1):64−71
[10]Du Y L,Wu Q X,Jiang C S,Xue Y L.Adaptive recurrent-functionallink-network control for hypersonic vehicles with atmospheric disturbances.ScienceChina,2011,54(3):482−497
[11]Wang P,Tang G J,Liu L H,Wu J.Nonlinear hierarchy-structured predictive controldesign for a generic hypersonic vehicle.ScienceChina Technological Sciences,2013,56(8):2015−2036
[12]Kanellakopoulos I,Kokotovic P V,Morse A S.Systematic design of adaptive controllers for feedback linearizable systems.IEEE Transactionson AutomaticControl,1991,36(11):1241−1253
[13]Koshkouei A J,Zinober A S I.Adaptive backstepping control of nonlinear systems with unmatched uncertainty.In:Proceedings of the 39th IEEE Conference on Decision and Control.Sydney,Australia: IEEE,2000.4765−4770
[14]Swaroop D,Hedrick J K,Yip P P,Gerdes J C.Dynamic surface controlfora class ofnonlinear systems.IEEETransactionsonAutomatic Control,2000,45(10):1893−1899
[15]Gao D X,Sun Z Q,Du T R.Dynamic surface control for hypersonic aircraft using fuzzy logic system.In:Proceedings of the 1st IEEE International Conference on Automation and Logistics.Jinan,China: IEEE,2007.2314−2319
[16]Utkin V.Variable structure systems with sliding modes.IEEE Transactionson AutomaticControl,1977,22(2):212−222
[17]Zhou Y X,Wu Y X,Hu Y M.Robust backstepping sliding mode controlof a class ofuncertain MIMO nonlinear systems.In:Proceedings of the 6th IEEE International Conference on Control and Automation. Guangzhou,China:IEEE,2007.1916−1921
[18]Zhu Kai,Qi Nai-Ming,Qin Chang-Mao.Adaptive sliding mode controller design for BTT missile based on backstepping control.Journal of Astronautics,2011,31(3):769−773(in Chinese)
[19]Plestan F,Shtessel Y,Bregeault V,Poznyak A.New methodologies for adaptive sliding mode control.International Journal of Control,2010, 83(9):1907−1919
[20]Park J,Sandberg I W.Universal approximation using radial basis function networks.Neural Computation,1991,3(2):246−257
[21]Cybenko G.Approximation by superpositions of a sigmoidal function. Mathematicsof Control,Signals,and Systems,1989,2(4):303−314
[22]Hornik K,Stinchcombe M,White H.Multilayer feedforward networks are universal approximators.Neural Networks,1989,2(5):359−366
[23]Hu Y N,Jin Y Q,Cui P Y.RBF NN-based backstepping control for strict feedback block nonlinear system and its application.Advances in Neural Networks ISNN 2004 Lecture Notes in Computer Science,2004, 3174:129−137
[24]Shaughnessy J D,Pinckney S Z,McMinn J D,Cruz C I,Kelley M L.Hypersonic Vehicle Simulation Model:Winged-cone Configuration, Technical Report TM-102610,NASA,USA,1990.
[25]Keshmiri S,Mirmirani M D.Six-DOF modeling and simulation of a generic hypersonic vehicle for conceptual design studies.Modeling and Simulation Technologies Conference and Exhibit,2004,1−12
[26]Slotine J E,Li W P.Applied Nonlinear Control.Englewood Cliff,NJ: Prentice Hall,1991.290−292
[27]Levant A.Higher-order sliding modes,differentiation and outputfeedback control.InternationalJournalofControl,2003,76(9):924−941

Jingmei Zhang Ph.D.candidate at the School of Automation,Southeast University.Her research interests include nonlinear control and flight control.

Changyin Sun Professor at the School of Automation,Southeast University.He received the Ph.D. degree in electrical engineering from the Southeast University in 2003.He has received National Outstanding Youth Science Foundation,the First Prize of Nature Science of Ministry of Education, China(2007),the Second Prize of Nature Science of Ministry of Education,China(2010)and Jiangsu Youth Science and Technology Award(2010).His research interests include intelligent control theory and its application,nonlinear system analysis and optimization,and pattern recognition.Corresponding author of this paper.

Ruimin Zhang Ph.D.candidate at the School of Automation,Southeast University.His research interests include nonlinear control and flight control.

Chengshan Qian Professor in the College of Information and Control,Nanjing University of Information Science and Technology.He received the Ph.D.degree in controltheory and controlengineering from the College of Automation Engineering, Nanjing University of Aeronautics and Astronautics in 2008.His research interests include nonlinear control and automatic detection technique.
t
October 28,2014;accepted March 24,2014.This work was supported by National Outstanding Youth Science Foundation (61125306),National Natural Science Foundation of Major Research Plan (91016004,61034002),Specialized Research Fund for the Doctoral Program of Higher Education of China(20110092110020),and Open Fund of Key Laboratory of Measurementand Controlof Complex Systems of Engineering (Southeast University),Ministry of Education(MCCSE2013B01).Recommended by Associate Editor Bin Xian
:Jingmei Zhang,Changyin Sun,Ruimin Zhang,Chengshan Qian. Adaptive sliding mode control for re-entry attitude of near space hypersonic vehicle based on backstepping design.IEEE/CAA Journal of Automatica Sinica,2015,2(1):94−101
Jingmei Zhang,Changyin Sun,and Ruimin Zhang are with the Flight Control Research Center,Key Laboratory of Measurement and Control of Complex Systems of Engineering,Ministry of Education,School of Automation,Southeast University,Nanjing 210096,China(e-mail:meizijingjing@163.com;cysun@seu.edu.cn;zhangrim@163.com).
Chengshan Qian is with the College of Information and Control,Nanjing University of Information Science&Technology,Nanjing 210044,China(email:qianchengshan@nuist.edu.cn).
 IEEE/CAA Journal of Automatica Sinica2015年1期
IEEE/CAA Journal of Automatica Sinica2015年1期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Autonomous Landing of Small Unmanned Aerial Rotorcraft Based on Monocular Vision in GPS-denied Area
- Adaptive Backstepping Tracking Control of a 6-DOF Unmanned Helicopter
- A Predator-prey Particle Swarm Optimization Approach to Multiple UCAV Air Combat Modeled by Dynamic Game Theory
- Guest Editorial for Special Issue on Autonomous Control of Unmanned Aerial Vehicles
- Continuous Sliding Mode Controller with Disturbance Observer for Hypersonic Vehicles
- Decoupling Trajectory Tracking for Gliding Reentry Vehicles
