感应电动机绕组与晶闸管角内接方式的软起动过渡过程分析及其控制

徐广源，彭 涛

（国家电网铜陵供电公司，安徽 铜陵　244000）

感应电动机绕组与晶闸管角内接方式的软起动过渡过程分析及其控制

徐广源，彭 涛

（国家电网铜陵供电公司，安徽 铜陵244000）

摘要：该文分析了三相交流调压电路在晶闸管与绕组内部角接电路结构下的系统工作状态，建立了各种工作状态对应的电机数学模型，总结了角内接模式与传统的星接和角外接模式的软起动过渡过程之间的异同点，并针对角内接模式进行了软起动控制试验.

关键词：感应电动机；软起动；角内接

三相感应电动机在全压起动时会产生很大的冲击电流，一般为额定电流的4-7倍，特别是对于大中型电动机来说，起动过程的冲击电流容易使得电网电压大幅下降，严重影响了系统中其它负载的正常工作.对于小型电动机来说，有的场合需要频繁启、停电动机，这样频繁起动和停机产生的冲击电流使得电机的绕组因过热而加速绝缘老化，缩短电动机的使用寿命.随着电力电子技术和控制理论的快速发展，异步电动机的软起动控制方法研究取得了长足的进步，并且已经在实际应用中取得了较好的效果，其中应用较为普遍的是基于晶闸管交流调压电路的软起动方式.虽然，变频器软起动器能获得比较理想的起动性能，但是对于一些无需调速的电动机来说并不适用，而且其成本较高，从而限制了它的推广.

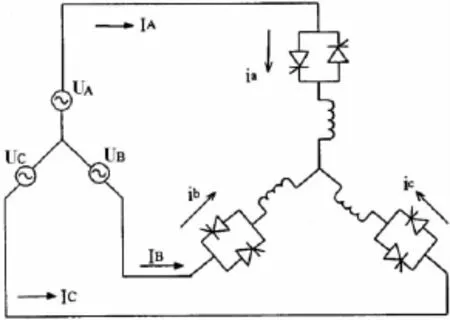
图1　绕组和晶闸管星型接法

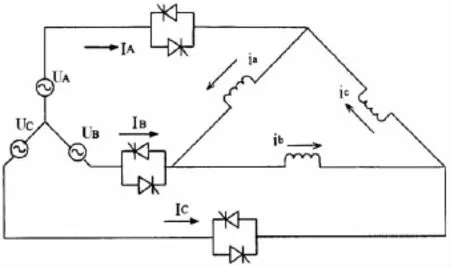
图2　绕组和晶闸管角外接

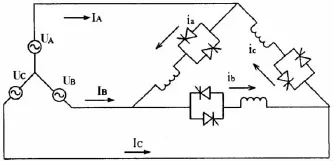
图3　绕组和晶闸管角内接

一直以来，人们研究和应用比较普遍的是将双向晶闸管或一对反并联晶闸管在电源侧外接串联于电动机绕组上的调压电路，分别如图1和图2所示，包含绕组内部星型接法和电机绕组内部角接两种方式.而对于如图3所示的电路，将晶闸管直接与电机每相绕组串联后再角型接法，称之为角内接方式，很少有人对其软起动的控制方法和软起动过程进行过研究［1］.本文正是针对这种角内接的调压电路，就其软起动过程中的各种工作状态和特点进行分析，并且结合各种软起动控制方法对其软起动的具体控制进行研究和试验.

1　角内接软起动控制系统原理分析

对于如图3所示的角内接软起动电路，为了便于分析，我们假定：

（1）电源为三相对称的正弦电压源，电源的内阻抗为零；

（2）6个晶闸管具有相同的特性，对称触发，关断状态时其阻抗为无穷大，导通状态时其阻抗为零；

（3）电机的参数全部为常数，忽略磁饱和；

（4）稳态运行时，异步电机的转速为常数；

（5）异步电机为理想电机，其定转子绕组在空间产生正弦分布的磁动势，转子绕组星接.

1.1角内接软起动控制系统的工作状态

对于电机绕组星接的方式，如图1所示，只存在5种工作状态［2］：

①三相电源同时导通，定子电流ia，ib，ic的瞬时值同时都不等于零；

②a相的电源关断，ia的瞬时值为零；

③b相的电源关断，ib的瞬时值为零；

④c相的电源关断，ic的瞬时值为零；

⑤三相电源同时关断，ia=ib=ic=0，由于这两种接法必须至少两相同时导通时才能形成回路，故任意两相电源关断时与三相电源同时关断的结果一致.

但是，对于角内接的连接方式而言，由于三相绕组与晶闸管一一串联形成角内接，其中任意一相晶闸管导通都可以与电源形成回路，在线路中产生电流.所以相对于前面所述的两种方式而言，其工作状态又增加了3种：

⑥a和b相同时关断，ia=ib=0；

⑦a和c相同时关断，ia=ic=0；

⑧b和c相同时关断，ib=ic=0。

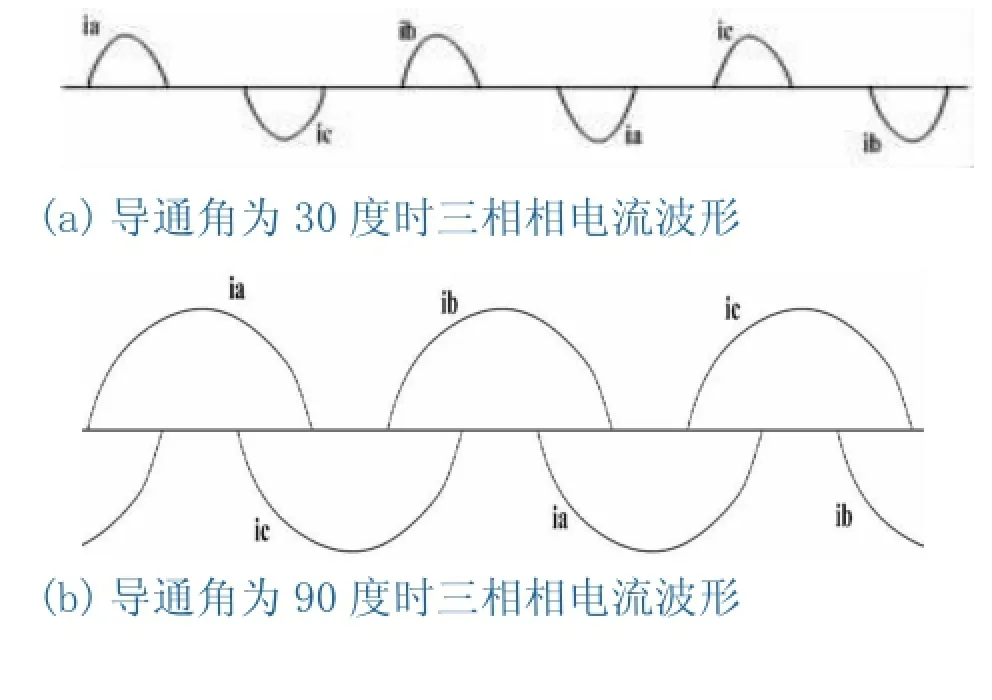
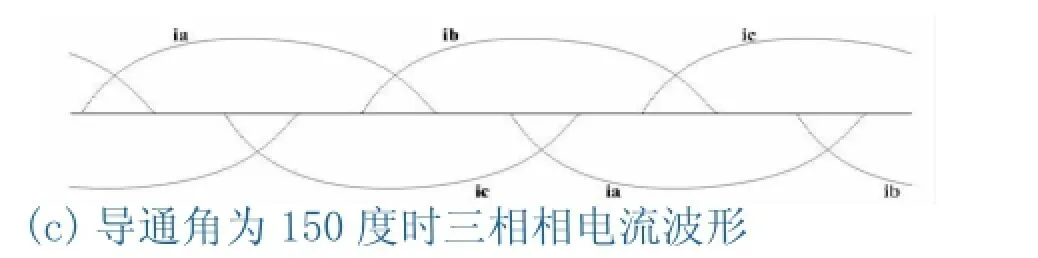
图4　导通角决定的相电流波形

对于三相角内接电机，只存在有晶闸管导通角决定的三种运行情况：

（1）导通角：0＜θ＜60o，如图4（a）所示，这种情况下，异步电机定子绕组或者只有一相导通电源，或者三相同时关断，其线电流是断续的；

（2）导通角：60o＜θ＜120o，如图4（b）所示，这种情况下，异步电机定子绕组或者两相同时，或者只有一相单独导通电源，其线电流是连续的；

（3）导通角：120o＜θ＜180o，如图4（c）所示，这种情况下，异步电机定子绕组或者三相或者两相同时导通电源，其线电流是连续的.

对于角外接方式来说，情况又不一样，由于三相绕组互相角接，晶闸管接在绕组外部，当线电流中有两相电流流过时，定子三相绕组中都有相电流流过，对于线电流来说，其具有与星接模式时相同的工作状态，对于相电流来说，只存在三相电流同时不为零和同时为零这两种状态.

图5　异步电机α、β、0轴等效电路

1.2角内接模式下电机模型

在图1所示的电路中，传统的电机模型采用相电压作为输入量，三相线电流之和接近于零，故在线电流中不存在零序电流.然而，对于角内接的模式，其数学模型采用线电压作为输入量，由于其结构的特殊性，三相绕组中的每相电流均是独立的，三相相电流之和不时刻为零，即在某些状态时三相相电流中存在零轴电流分量，但是由于绕组的对称性，零轴分量并不在线电流中出现［1］.图5为电机绕组和晶闸管角内接的情况下以α、β、0坐标系为参考的等效电路，假定α轴与a向绕组轴线重合，β轴在空间上超前α轴弧度，图5（c）是0轴分量的等效电路，其定、转子等效电路之间并无耦合关系.定转子各量的矩阵方程如下：

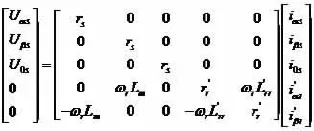
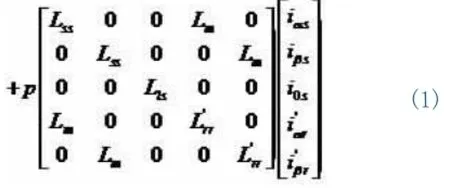
异步电机的电磁转矩为：

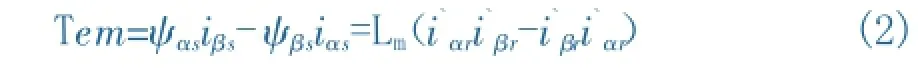
其中，Uαs、Uβs、U0s和iαs、iβs、i0s分别为α、β、0轴的电压和电流，i`αr、i`βr为折算到α、β轴后的转子相电流，Lls为定子漏电感，L`lr为折算到定子侧的转子漏电感，Lm为定转子互感，且 Lss=Lm+Lls，L`rr=Lm+L`lr，ωr为转子的电角速度，p为微分算子。

（1）式可以简化为：

因为异步电机转子一般均短接，所以一般均有Uαr=Uβr=0，由于零轴电流所产生的气隙合成磁场为零，仅产生与电枢绕组交链的漏磁场，因而不参与电磁功率的转换，所以角内接时每相绕组中流动的零序电流并不产生任何电磁转矩［3］，如式（2）所示。对于2.1中所述的八种工作状态，根据晶闸管的触发和关断状态的约束条件，以及电压电源和Uαs、Uβs之间的关系，即可计算角异步电机绕组与晶闸管串联角内接方式的软起动过渡过程［2］.

1.3系统状态方程分析

在角内接模式下，对于状态①，由于三相绕组电流瞬时值都不等于零，系统状态方程此时与式（1）相同，此时由于电源和绕组的对称，相电流和线电流中均没有零轴分量产生.

对于状态②，a相电源关断，a相定子电流的瞬时值为零，a相晶闸管进入阻断状态，此时的电路结构可以简单等效为图（6）所示的电路.根据电路基本原理分析可知，定子相电流ia=0，ib和ic幅值相等，相位相差120o，故零轴电流.由于采取的α、β、0坐标系，α轴与a相绕组轴线重合，故有：ia=iαs+i0s=0。此时定子a相的电压是定子α轴和0轴电压之和，即Ua=Uαs+U0s=p（Lmi`α r-Lssi0）s.不计零轴分量时，对应于状态②的定转子各量矩阵方程为：

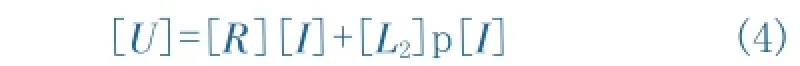
其中

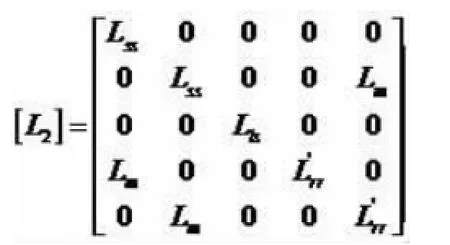
对于状态⑤，由于导通角很小，所以出现了三相绕组的电流同时为零的情况.这段时间内，由于电流在短路的转子绕组中继续流动，所以通过互感作用，还会在定子绕组中出现感应电压，由式（1）得：iα s=iβs=0，Uα s=pLmi`αr，Uβs=pLmi`β r［2］.此时相电流中没有零轴分量。对应于状态⑤的定转子各量矩阵方程为：

其中

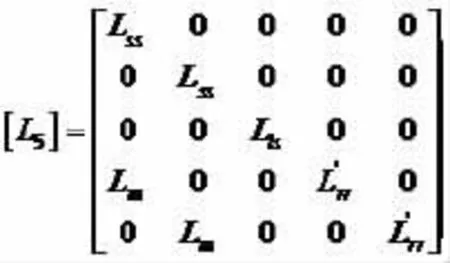
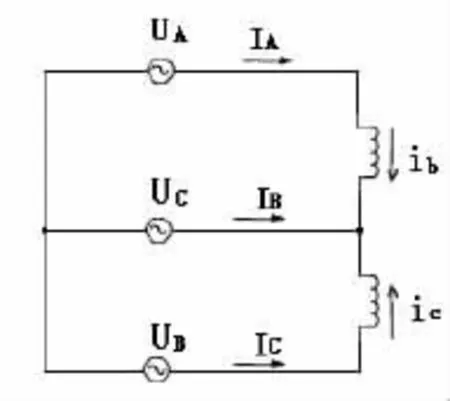
图6　角内接在状态②时的等效电路

对于状态⑧，b相和c相的定子电流同时为零，故此时iβs=0，Uβs=pLmi`β r，此时相电流中有零轴分量，i0s=is/3.对应于状态⑧的定转子各量的矩阵方程为：

其中

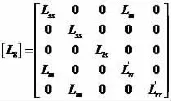
由于状态③④与状态②相似，状态⑥⑦与状态⑧相似，其状态对应的定转子各量矩阵方程可以通过类似的方法分析出来.通过分析，发现在软起动过程中由于电源出现不对称的情况导致电机的定转子各量矩阵方程中的电感矩阵发生变化.对于星接模式来说，对应的五种工作状态中都不会在相电流中出现零轴分量.对于角外接模式来说，由于线电流流过两相电流时，三相绕组相当于一相绕组与另外两相串联的绕组并联，显然三相相电流之和不为零，故在相电流中出现零轴分量.对于角内接模式来说，根据前面的分析可知在状态②③④和⑥⑦⑧时在相电流中都会出现零轴分量.有了不对称情况下的电机模型，就能够推导出一系列软起动初始触发角，有效地抑制由于初始角度选择不当造成的基频电磁转矩的振荡.

2　应用试验结果及分析

对于图1和图2所示的应用较为广泛的晶闸管调压电路，人们对其软起动控制方式的研究很多，也取得了许多显著的成果.实际软起动控制中应用较多的控制方法有：电压斜坡控制、限流控制、转矩控制和功率因数角控制等方法［4］［5］［6］.对于图3所示的角内接软起动控制电路结构，人们在实际中研究和应用的比较少.由于这几种电路结构和工作原理的相近性，使得它们的控制原理和方法存在着较大的通用性，只是在一些细节方面存在着一定的差异.下面就异步电动机晶闸管与电机绕组角内接的方式进行软起动控制试验.

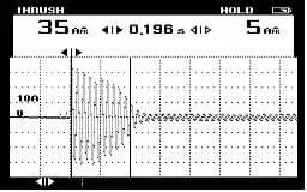
图7　全压起动冲击电流实测波形

对额定功率2.2KW三相异步电动机，在空载的情况下，就晶闸管与绕组角内接方式进行了限流软起动和功率因数角闭环软起动控制方法的试验.

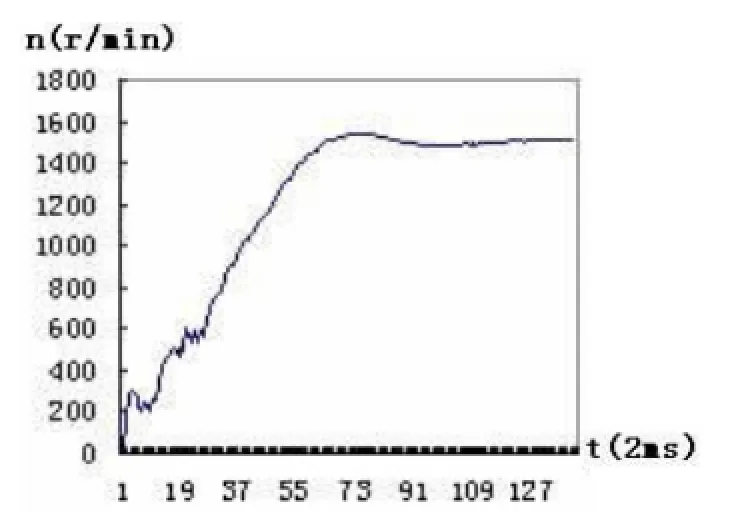
图8　全压起动实测转速波形

2.1全压起动

如图7和图8所示，分别为2.2KW电机在空载情况下角接全压起动时测量的实际相电流和转速波形.该电机额定电流为 4.8A，额定转速为1450r/min.全压起动时其相电流峰值最大值达到35A，约为额定电流峰值的5.2倍，如图7所示.起动过程中由于定子瞬态直流分量的影响，其转速和电磁转矩出现了大幅的基频振荡［7］.

2.2限流软起动

如图9和图10所示，分别为2.2kw电机在空载情况下限流软起动时的相电流和转速波形，其限流值为2In，大小约为10A左右.这种方法能够有效地控制起动电流，但是起动时间比较长，且起动过程中容易产生电流和转矩的振荡［8］.

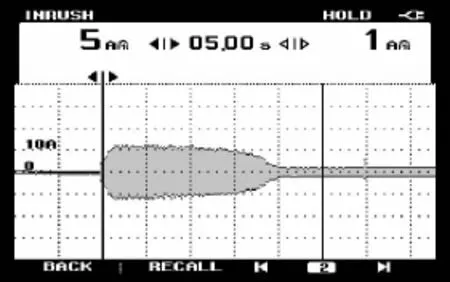
图9　限流软起动实测电流波形

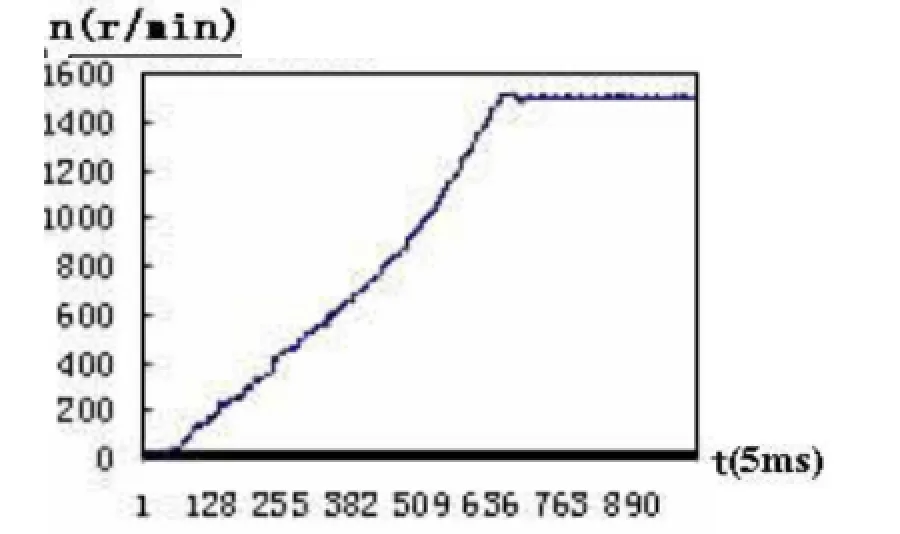
图10　限流软起动实测转速波形

2.3功率因数角闭环软起动

如图11和图12所示，为2.2KW电机在空载情况下的功率因数角闭环软起动电流和转矩波形.试验中通过相位检测电路实时检测相电压和相电流的相位差—可检测功率因数角，由于电机绕组端电压是触发角α和可检测功率因数角φ的函数，即U=f（α，φ），单片机根据实时检测的φ角和给定的α角即可计算得出维持相邻两个周期的电机绕组电压呈规律性变化的触发角调整量α，这种方法有效的避免了由于起动过程中电流和转矩的振荡［6］.

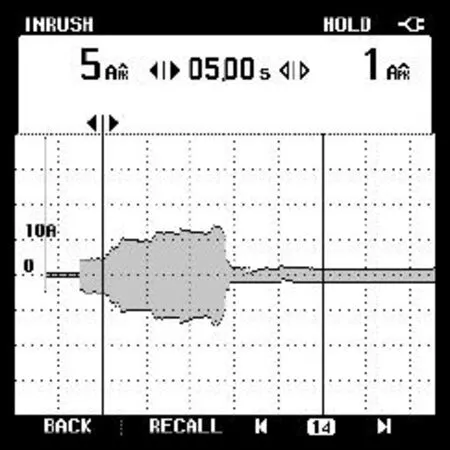
图11　功率因数角闭环软起动实测电流波形

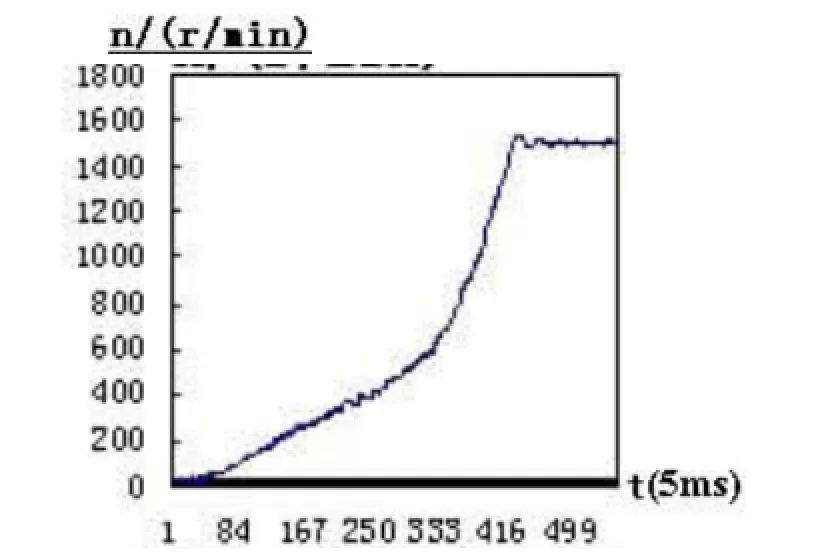
图12　功率因数角闭环软起动实测转速波形

3　结论

本文重点分析了异步电机绕组与晶闸管角内接电路结构下的系统工作状态，对系统处于各种工作状态时的电机模型进行了研究，并且针对角内接电路进行了软起动控制试验，得到了良好的试验效果，得出如下结论：

（1）角内接模式的系统工作状态与星接和角外接模式相比更加复杂，多了三种状态，即存在三相的单相绕组中流过电流的三种状态；

（2）星接模式和角外接模式下，绕组的线电流中均不存在零轴分量，而在角内接模式下，对应于状态②③④和⑥⑦⑧，相电流中存在零轴分量；

（3）由于角内接模式电路结构的特殊性，使得其控制器件流过的电流是相电流，比角外接模式承受的线电流小，因此晶闸管的器件选择空间更大.

综上所述，由于异步电机绕组和晶闸管角内接的交流调压电路结构本身的工作特点，使得在软起动控制和调压控制时电路结构和控制方法设计更加丰富.

参考文献:

［1］David Gritter，Dora Wang，Thomas G Habetler.Soft starterinside Delta Motor Modeling and Its Control. Industry Applications Conference.2000.Conference Recordofthe2000IEEE Volume2，8-12Oct.2000.

［2］高景德，张麟征.电机过渡过程的基本理论及分析方法（下册）［M］.北京：科学出版社，1983.

［3］马志云.电机瞬态分析［M］.北京：中国电力出版社，1998.

［4］Venkata V.sastry，M.Rajendra Prasad，T.V.Sivakumar. Optimal Soft Starting Voltage-Control-Fed IM Drive BasedonVoltageAcrossThyristor.IEEETranslations onPowerElectronics，VOL.12，NO.6，November1997.

［5］ZenginobuzG，CadirciI，ErmisM，etal.Softstarting of large induction motors at constant current with minimized starting torque pulsation.Industry Applications Conference，2000.Conference Record of the 2000IEEE，200，3:1593-1604.

［6］王毅，赵凯岐，徐殿国.电机软起动控制系统中功率因数角的研究［J］.中国电机工程学报，2002，（8）.

［7］汤蕴璆，张奕黄，范瑜.交流电机动态分析［M］.北京：机械工业出版社，2004.

［8］王玉峰，马广程，王常虹，等.晶闸管控制感应电机起动过程中振荡现象研究［J］.电机与控制学报，2002，（3）.

责任编辑：张隆辉

中图分类号：TM 346

文献标识码：B

文章编号：1672-2094（2015）02-0148-05

收稿日期:2014-12-15

作者简介：徐广源（1981-），男，安徽池州人，国家电网铜陵供电公司工各程师，硕士.彭涛（1980-），男，安徽安庆人，国家电网铜陵供电公司工各程师，硕士.