小学数学“立美”教学模式初探

谭习龙

我们在立美教育理念下构建了如下数学课堂教学模式：

复习铺垫，展开审美想象——赏美

?                              ?

创设情境，诱发审美注意——启美

?                              ?

探究发现，丰富审美感知——求美

?                              ?

实践应用，激发审美创造——创美

?                              ?

回顾小结，提高审美素养——立美

复习铺垫，展开审美想象——通过复习铺垫旧知，让学生展开审美想象，在欣赏美中，促进迁移。

创设情境，诱发审美注意——通过创设美的学习情境，寓教于乐，诱发审美注意，激发学生强烈的好奇心，形成积极探究的心理倾向。这一过程重在启美。

探究发现，丰富审美感知——通过引导学生动手实践、合作交流、自主探究，借助形象直观的教学手段，丰富审美感知，从而发现规律，使学生不仅掌握了新知，受到了美的启迪，更丰富了内心世界，得到了更全面的发展。这一过程重在求美。

实践应用，激发审美创造——通过引导学生运用新知，解决问题。在一题多解、一题多变，一法多用、一图多变等美的熏陶中，鼓励学生多向思维，标新立异，不断去追求解法的优化，结论的美化，得到愉悦的享受，从而激发学生的审美创造，促进新知的内化。这一过程重在创造美。

回顾小结，提高审美素养——通过回顾小结，将知识与美水乳交融，使知识得以升华，审美素养得以提高，情感得到陶冶。

现以国标本苏教版第十二册教材“解决问题的策略”为例，谈谈如何在小学数学教学中构建“立美”教学模式。

一、复习铺垫，展开审美想象——赏美

我们已学过哪些解决问题的策略？那么今天我们又要学习什么策略呢？

[设计意图：通过复习铺垫，让学生展开审美想象，促进迁移。]

二、创设情境，诱发审美注意——启美

同学们，这是一幅丹阳市的地图，是我们美丽的家乡，从地图上你有办法计算出“全市的面积大约有多大吗？”

[设计意图：通过创设学生感兴趣的美的学习情境，诱发审美注意，促使学生带着疑问和浓厚的兴趣进入本节课的学习，形成积极探究的心理倾向。这一过程重在启美。]

三、探究发现，丰富审美感知——求美

（一）观察比较，感知“转化”策略

1.请同学们看屏幕，谁能一眼看出下面两个图形哪个面积大？

（1）猜猜看？

（2）验证。

（3）大组交流。

2.刚才我们通过平移和旋转把这两个左边的图形都转化成右边面积与它相等的长方形，从而比较了这两个图形的大小。

这里都运用了什么方法呀？

想一想，为什么要做作这样转化呢？

那你感觉到这样转化有什么好处？

回顾刚才的转化过程，什么变了？什么没有变？

[设计意图：通过比一比、画一画、算一算，引导学生动手实践、合作交流、自主探究，借助形象直观的教学手段，将不规则的图形转化成规则的图形，丰富了审美感知，从而发现方法，让学生感受到：通过转化可以化繁为简，从而初步感知“转化”策略的含义、方法与价值，获得解决问题的成功感。]

（二）回顾交流，体验“转化”策略

1.请同学们回顾一下，我们在以前的学习中运用转化的策略解决过什么问题？（提示：可以从面积、体积公式的推导，以及小数、分数四则运算等方面思考。）

学生充分列举，教师课件演示。

现在我们把这些转化过程都列举出来，比较一下，你发现它们什么共同的地方？

[设计意图：通过合作交流、借助形象直观的教学手段，引导学生总结回顾在过去的学习中，曾经运用转化的策略解决过的问题，丰富了学生的审美感知。从策略的高度重新建立相关知识间的联系，即解决一个新问题通常是想办法把它转化为一个熟悉的，已解决的问题，从而使学生恍然大悟，逐步深化对转化策略的认识，突出转化策略的价值。使学生不仅掌握了新知，受到了美的启迪，更丰富了内心世界，得到了更全面的发展。这一过程重在求美。]

四、实践应用，激发审美创造——创美

（一）巩固练习，运用“转化”策略

（1）先观察，你有办法一眼看出涂色部分占整个图形面积的几分之几吗？

想不想来挑战一个难度大点的？

回顾刚才解决这个问题的过程，你有什么收获？

小结：这里既可以从涂色部分入手，也可以反过来从空白部分入手，由研究涂色部分转化为研究空白部分。给我们这样的启发：看来有很多问题从正面解决很麻烦，但如果转化成从反面思考的话，要简单多了。

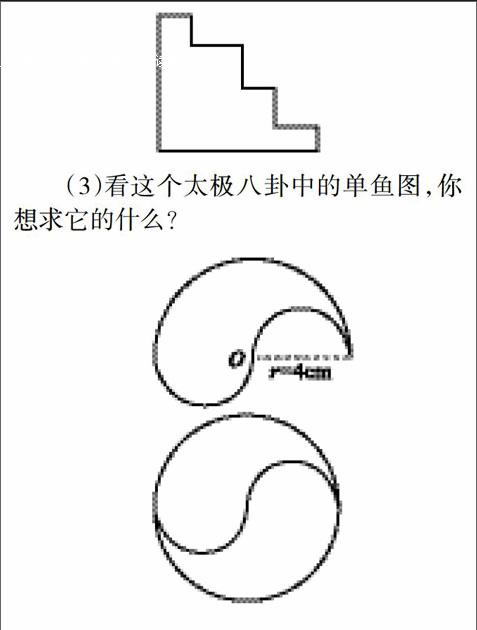
（2）出示：求下面不规则图形的周长，你觉得至少要量出几条边的长度？

（3）看这个太极八卦中的单鱼图，你想求它的什么？

师：怎么样你就容易求它的周长了？从求周长算式中，你发现什么？（可见转化方法不同，计算速度也不同）

怎么就容易求它的面积了？

小结：我就不明白了，这个图形为什么求周长时要转化为圆形，而求面积时要转化为半圆呢？（第一种转化前后图形的周长相等，第二种转化前后图形的面积相等）所以我们以后在转化时要注意 （等量转化）。

（4）+++

这四个加数有什么特点？如果继续加，加几？再加？

我们回顾一下，刚才解决这 个问题的过程，你有什么感受？

小结：同学们，这是一道计算题，我们却借助图形来计算，这是一道加法题，我们还可以用减法来计算，看来我们要具体问题具体分析，从不同的角度来进行转化。

[设计意图：通过让学生经历多种形式的转化：形与形之间的转化（等积转化、等周转化等） ，数与形的转化 （包括数与计算方面的转化等），让学生明白数学学习就是不断转化的过程，数学问题都可以在已具备的知识和经验的基础上实现“化繁为简、化新为旧”的等价转化。在一题多解、一题多变，一法多用、一图多变等美的熏陶中，鼓励学生多向思维，标新立异，不断去追求解法的优化，结论的美化，得到愉悦的享受，从而激发学生的审美创造，促进新知的内化。这一过程重在创造美。]

（二）联系生活，深化“转化”策略

其实，转化在我们日常生活中有着十分广泛的运用，

大家都熟悉的曹冲称象的故事里就用到了转化。同学们觉得曹冲怎么样？他聪明在哪里？

生活中还有很多地方需要运用转化策略的，例如：如何求土豆的体积？一张纸的厚度？硬币的体积？计算淘汰赛要比赛多少场的问题。

哪你有办法求出丹阳市的面积大约有多大吗？

我们不妨可以用数学家于振善的方法来巧“称”地图面积。

他先把地图按边界描在一块厚度均匀的木板上，而后把这块图形锯下来，称出它的重量是159克，随后，把地图中代表一定长度和宽度的一块长方形如10千米长、5千米宽也锯下来，也用秤来称是7.5克。因为厚度一定，两者的重量比就是面积比，就是159：7.5大约是21：1。而长方形所代表的面积是50平方千米，所以，全市的土地面积大约是50×21=1050平方千米。于振善巧“称”地图面积，将面积比巧妙转化成重量比，已成为数学史上一段佳话。所以当我们遇到困难或者难以解决的问题的时候，可以从不同的角度进行转化，就会给我们的学习和生活带来好处。

[设计意图：通过重温曹冲称象和照应了开头的称地图面积的故事等问题，使学生在已具备的知识和生活经验的基础上，实现等价转化，从而解决问题。将学生的眼光再次拉向了现实生活，一方面调动了学生学习的积极性，丰富了学生对转化策略的认识，另一方面使学生体验到生活与数学的密切联系，感受转化策略在实际生活中应用的广泛性，渗透了化归的数学思想，即解决任何数学问题都是一个未知向已知的转化过程。体现了数学的工具性和它的人文价值。让学生享受到数学的简洁、神奇美]

五、回顾小结，提高审美素养——立美

小结：对于转化，你有什么新的体会？

……

师：很多数学家都这样认为：解题就是把新题目转化为已经解过的题。学习数学的过程就是不断转化的过程。将复杂转化为简单，陌生转化为熟悉，未知转化为已知。所以说在解决数学问题时转化是无处不在的。

（总评：本课先以生活中运用转化策略解决问题的策略问题导入课堂，激发了学生学习的内驱力;通过例1的探索，让学生明确：当一个问题比较复杂，需要将其等价转化为简单的问题来解决;接下来通过对以往数学学习中众多转化过程的分析，帮助学生感受转化策略运用的广泛性，体会转化的实质及其蕴涵的数学思想，从而明确：遇到新知识时，可以想办法转化为以前学习过或是解决过的旧知。体验运用转化策略的目的，最后通过大量形式多样的练习，使学生明确：直接解决一个比较困难甚至是无法解决的问题时，可以换一个角度思考，从而间接解决这个问题。整个过程将知识与美水乳交融，由此促使学生掌握实施转化策略的方法，体会到转化的魅力，使知识得以升华，审美素养得以提高，情感得到陶冶，增强了学好数学的自信心。

【作者单位：丹阳市访仙中心小学  江苏】