Landau-Lifschitz方程的反散射变换微扰理论
李 存,宋宣玉, 王林生,刘墨林
(1.信阳师范学院 物理电子工程学院,河南 信阳 464000;2.河南工业职业技术学院 电子工程系,河南 南阳 473000)
0 引言
完全各向同性Landau-Lifschitz方程的孤子解已经通过反散射变换理论建立了相应的求解方法[1-4].完全各向同性的情况毕竟是一种理想化的模型,在实际问题中因为某些实际因素使得方程往往含有修正项,这时严格的求解一般是不可能的.当实际系统与理想化模型之间存在的差异比较细微,修正项可以视作一小量时,建立相应的适用的微扰方法就成为解决此类问题必要的、可行的方法,具有更为实际的意义.对于非线性方程系统的微扰方法,目前已经建立了多种研究方法,例如:Keener、Mclaughlin等在处理Sine-Gordon方程的微扰问题时建立的直接微扰理论[5-6],这种方法意在强调直接微扰方法与基于反散射变换方法的理论的不同,刻意避免使用反散射变换理论所得出的结果.虽然这种方法的建立解决了非线性方程系统的一系列微扰问题,但是所得到的基本解的完备性无法得到完整的证明.后来,Mann等人通过线性微分方程中的格林函数方法证明了单孤子情况下的完备性[7],使得直接微扰方法更加完善,从而解决了非线性方程系统的诸多微扰问题[8-11].对于Landau-Lifschitz方程的微扰理论,我们也曾尝试直接微扰的方法,由于Landau-Lifschitz方程存在3个自旋分量,导致方程在展开过程过于烦琐而达不到预期的效果.本文是建立在反散射方法为基础上的微扰方法[12],这种方法最大的优点是在建立过程中保留了反散射变换方法所得到的基本解,不需要通过其他方法再去求解齐次线性化方程的解,在非线性系统中是比较普遍使用的.
含修正项的Landau-Lifschitz方程可以表述为
St+S×Sxx=εP(S).
(1)
其中:ε是一个比较小的实参量,P(S)为修正项.当ε为零时,式(1)即为完全各向同性Landau-Lifschitz方程.而相应的由微扰理论得出的解在ε为零时即为不含修正项也即完全各向同性Landau-Lifschitz方程的解.
反散射变换方法解法要点是首先引入一对Lax方程,利用它们的相容性条件给出当且仅当谱参数独立于时间t时方程的Jost解.在建立反散射变换方法时,首先从第一个Lax方程出发求得满足方程的解,通过求解过程中所引入Jost解的解析性、渐进行为建立反散射方程.而在确定散射数据随时间的演化方程时,基于谱参数λ独立于时间t的条件利用第二个Lax方程求解[1,12].
在利用反散射方法建立含修正项的Landau-Lifschitz方程的微扰理论时,依然基于谱参数λ独立于时间t的条件从而保留第一个Lax方程,暂时不考虑第二个Lax方程,否则所得的含修正项的结果无法与完全各向同性时的反散射变换方法的结果保持一致.这样就使得在建立Landau-Lifschitz方程的微扰理论时所引入的Jost解及其渐进行为与完全各向同性时的结果一致,反散射方程也保留了完全各向同性时的形式.
1 与时间相关的Jost解
不含微扰项的Landau-Lifschitz方程的两个Lax方程为
∂xψ(x,λ)=L(x,λ)ψ(x,λ),
(2)
∂tψ(x,λ)=M(x,λ)ψ(x,λ).
(3)
其中:式(2)中L=-iλS·σ;式(3)中M=-i2λ2(S·σ)+λ(S·σ)(SX·σ).完全各向同性Landau-Lifschitz方程与Nonlinear Schrodinger方程具有规范等价性[12],故而Landau-Lifschitz方程含时间的Jost解如同Nonlinear Schrodinger的Jost解一样[4,12],可以表示为
(4)
其中,h(t,λ)=e-i2λ2t.在含微扰情况下,确定了谱参量以及散射数据随时间的演化关系,由反散射方程得到的解才能表示为含时间t的确切函数.这时的散射数据的结果与完全各向同性的结果只差ε阶的小量,定义
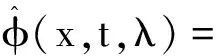
(∂t-M(x,t,λ))h(t,λ)φ(t,λ)≠0,
(5)
算子∂x-L(x,λ)作用于式(5)得到
(∂x∂t-M∂x-Mx-L∂t+
LM)h(t,λ)φ(x,λ).
(6)
因为∂x∂t=∂t∂x, 式(6)的等式右侧即
(Lt-Mx+[L,M])h(t,λ)φ(x,λ).
(7)
其中
Lt=-iλ(S·σ)t-iλt(S·σ),
(8)
式(8)代入式(7)可得
(Lt-Mx+[L,M])h(t,λ)φ(x,λ)=
(-iλ(S·σ)t-Mx+
[L,M])h(t,λ)φ(x,λ)-
iλt(S·σ)h(t,λ)φ(x,λ)=
(-iλ(S·σ)t-Mx+[L,M]-
εQ(S)h(t,λ)φ(x,λ)+(-iλt(S·σ)+
εQ(S))h(t,λ)φ(x,λ).
(9)
基于反散射变换方法,在式(9)中引入了Q(S)=-iλσ·P,而式(9)等式右侧第一项因为式(1)而只保留后一项.式(6)即为
G(x,λ)h(t,λ)φ(x,λ).
(10)
其中
G(x,λ)=-iλt(S·σ)+εQ(S).
(11)
这样就确定了含有修正项的Landau-Lifschitz方程含时间t的Jost解所满足的Lax方程.
2 以反散射变换为基础的微扰方法
为了确定散射数据随时间的演化,考虑边界情况,当x→-∞时,
∂t-M(x,t,λ)=∂t-i2λ2(S·σ),
(12)
(13)
x→-∞时,S·σ→σ3,在此极限下
(14)
并且,x→-∞时,
(15)
代入到式(14)得到
(16)
也即
(17)
另外,式(10)是非齐次方程,它的解可以表示为相应的齐次方程的线性组合

β(x,λ)φ(x,λ),
(18)
将式(18)代入到式(10),且左乘iφ(x,λ)Tσ2并考虑到a(λ)=det(φ(x,λ),ψ(x,λ))即可得到
ax(x,λ)=
ia(λ)-1φ(x,λ)Tσ2G(x,λ)·
h(λ)φ(x,λ).
(19)
同样,左乘iψ(x,λ)Tσ2得到
βx(x,λ)=
-ia(λ)-1ψ(x,λ)Tσ2G(x,λ)·
h(λ)φ(x,λ).
(20)
分别对式(19)和式(20)对x从-∞→x积分,考虑到边值问题得到
a(x,λ)=
φ(y,λ)dy,
(21)
β(x,λ)=
φ(y,λ)dy,
(22)
于是,当x→-∞时,
(23)
与式(17)比较得到
h(λ)at(λ)=β(∞,λ)a(λ),
(24)
h(λ)(bt(λ)-i4λ2b(λ))=
a(∞,λ)+β(x,λ)b(λ).
(25)
结合式(24)和式(25)得到
at(λ)=

(26)
bt(λ)-i4λ2b(λ)=

b(λ)ψ(λ))Tσ2G(x,λ)φ(x,λ)dx.
(27)
式(27)即含修正项Landau-Lifschitz方程以反散射方法为基础的微扰方法的基本方程,也是确定谱参量以及散射数据随时间演化关系的关键.对于λ连续谱的情况,入射波和散射波有相同的波数,λ是不依赖于时间t的,故而λt=0,G(x,λ)=εQ(x).
3 分离谱λn随时间的演化
对于束缚态,尽管谱参数λn的值将随时间发生变化,但仍然满足a(λn)=0,于是φ(x,λn)=bn(t)ψ(x,λn)并且对于任意的时间t都是成立的,所以at(λn)=0.这些条件说明了微扰项的存在并不改变散射问题的束缚态解,也就是不改变非线性方程的孤子解的形式.式(26)和式(27)的函数可以解析延拓到复平面的上半平面,所以在λ→λn时的极限成立.于是可得

(28)
由于G(x,λn)=-iλnt(S·σ)+εQ(x)是在束缚态下成立的,连续谱的情况应该满足G(x,λ)=εQ(x),代入式(26)可得


(29)
由第一个Lax方程得到
∂xφ(x,λ)=-iλ(S·σ)φ(x,λ),
(30)

(31)

(32)
将第一个Lax方程在λ和λn式相减,对λ取微商,再取λ=λn积分得到

φ(x,λn)dx.
(33)
结合式(29)得到
(34)
式(34)表明了当存在修正项时谱参数λn随时间的变化规律.而在ε→0的极限时,显然有λnt=0,正是完全各向同性Landau-Lifschitz方程的谱参量随时间演化的结果.
4 bn(t)随时间的演化
关于bn(t)随时间的演化问题,出发点是式(25),Jost解φ(x,t,λ)和ψ(x,t,λ)随时间的演化关系是确定的,因此,它们的比例关系bn(t)随时间的演化关系也是确定的,类似于式(5),定义
(∂t-M(x,λn))h(λn)-1ψ(x,λn).
(35)
式(25)变换为
h(λn)φ(x,λn)=
h(λn)2bn(t)h(λn)-1ψ(x,λn).
(36)
以算子∂t-M(x,λn)作用于式(36)得到
(37)
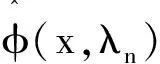
(38)
因此
βx(x,λn)φ(x,λn)=
G(x,λn)h(λn)φ(x,λn).
(39)
另因a(λn)=φ1(λn)ψ2(λ2)-φ2(λn)ψ1(λn),
于是
(40)

(41)
将式(41)积分得到
φ(y,λn)dy.
(42)
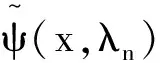
G(x,λn)h(λn)-1ψ(x,λn).
(43)
如同式(38)的处理方法,
(44)
可得到
γx(x,λn)ψ(x,λn)=
G(x,λn)h(λn)-1ψ(x,λn).
(45)

(46)
积分式(46)得到
ψ(y,λn)dy
(47)
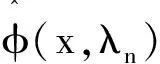
(48)
式(48)即反散射变换方法为基础的微扰理论的bn(t)随时间演化的基本方程.由于,
G(x,λn)=-iλnt(S·σ)+εQ(x),
且当x→∞时,S·σ=σ3,因此
(49)
由第一个Lax方程可得
(50)
和
(51)

(52)
对式(52)从-∞→∞积分,在束缚态情况下,显然结果为零.于是得到
φ(x,λn)dx=0.
(53)
式(48)即可简化为
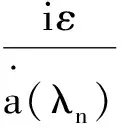
(54)
式(54)当ε→0时不含修正项,也就是完全各向同性时的结果.
5 结论
本文在完全各向同性方程反散射变换所得到的Jost解的基础上,在建立含修正项的Landau-Lifschitz方程的微扰理论时,除了推导过程尽可能的详尽外,在不引入任何超出通常反散射变换方法的前提假定下,关于散射数据bn(t)对时间的演化方程也作了合理的改进,并导出了谱参量以及bn(t)随时间的具体演化公式.这个结论对于今后利用反散射变换方法处理含修正项的Landau-Lifschitz方程奠定了基础.若代入相应的Jost解则可以从Zakharov-Shabat反散射变换方程得到相应非线性方程的一级近似解以及谱参量λ随时间的缓慢变化规律和非线性方程孤子解的形状变化,也为研究复杂的非线性方程提供了新的思路.

