基于交路接续的动车组运用计划优化模型与算法

李建，林柏梁*，耿令乾，陈雷，王家喜，武建平

(1.北京交通大学交通运输学院，北京100044；2.沈阳铁路局运输处，沈阳110001)

基于交路接续的动车组运用计划优化模型与算法

李建1，林柏梁*1，耿令乾2，陈雷1，王家喜1，武建平1

(1.北京交通大学交通运输学院，北京100044；2.沈阳铁路局运输处，沈阳110001)

针对动车组运用计划优化编制的问题，本文采用接续网络的方法，构建了动车组运用计划优化编制的0-1整数规划模型.该模型在动车组初始运用状态和历史检修数据的基础上，以动车组担当交路的接续时间总和最小化和动车组检修前累计运行里程最大化为优化目标，以动车组检修里程周期和动车组交路接续时间标准为主要约束，并充分考虑动车组与交路的匹配关系，以及客流高峰时期增加开行交路的情况.在模型的求解方面，本文基于粒子群算法设计了模型的求解策略.最后通过算例分析验证了模型与算法的有效性，为动车组运用计划的优化编制提供参考依据.

铁路运输；动车组运用计划；交路接续；0-1整数规划模型；粒子群算法

1 引言

随着我国高速铁路的发展，投入运营的动车组数量逐渐增多.优化编制动车组运用计划，对于加强动车组管理，提高其运用效率，降低运用和检修成本具有重要意义.

在该方面的研究中，国外的ErwinAbbink等人以荷兰铁路短缺能力最小化为目标，考虑动车组车型等因素，构建了动车组分配的优化模型[1].Luis Cadarso等人将动车组分配与交路计划优化结合起来进行优化研究[2].Giovanni Luca Giacco等人从动车组担当运输任务、检修和空驶等方面研究了动车组车底周转与检修计划[3].国内大多以列车运行线和交路生成为基础，将动车组周转运用问题转化为TSP问题进行研究[4,5].苗建瑞等人将交路计划归结为带补给的多人旅行商问题，以动车组数量最少化为目标构建优化模型，设计了分层优化的启发式算法[6].李华将动车组运用计划分为交路计划和检修计划，进而予以分别优化[7].王忠凯等人从动车组运用和检修计划一体化编制的角度构建了优化模型，并设计了模拟退火算法[8].在现有研究的基础上，本文基于动车组交路接续的思想，对动车组运用计划优化编制方法进行研究.

2 动车组交路接续网络

本文旨在通过动车组交路接续网络确定每列动车组担当交路的接续关系及检修作业的安排，因此构造了动车组交路接续网络，如图1所示.图中以动车组担当的交路和两次交路接续之间检修作业为节点，以动车组在交路之间的接续关系为弧.同时，为了表示计划的开始和结束状态，分别设置虚拟开始节点和虚拟结束节点.

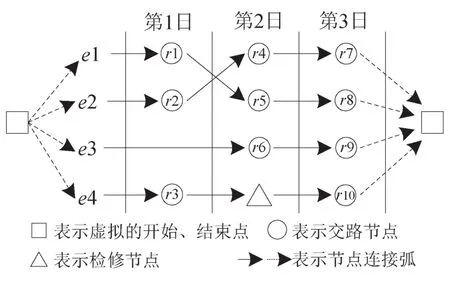
图1 动车组交路接续网络Fig.1 Route connection network of motor trainset

结合动车组交路接续网络，定义计划编制周期集合D={d|d=1,2,…,ND}，d为日期索引，ND为计划天数；动车组集合E={k|k=1,2,…,NE}，k为动车组索引，NE为动车组数量.将网络中的交路划分为虚拟初始交路、计划开行交路、虚拟结束交路三种类型，每条交路都有一个开始时间和结束时间.按交路开始时间进行先后排序，并根据排序结果给每条交路设定一个编号.基于此，定义交路集合W=W1⋃W2⋃W3，W1、W2和W3分别为三类不同交路的集合.虚拟初始交路集合W1={} 1,2,…,NE，即将每列动车组的初始状态看作一条交路；计划开行交路集合W2={} NE+1,NE+2,…,NE+NR，NR表示计划开行交路数量，由于高峰客流时增加开行交路，每天交路数量不尽相同，令NR(d)为第d天开行交路数量，则；虚拟结束交路集合W3={}NE+NR+1,NE+NR+2,…,2NE+NR，其数量等于动车组数量NE.因此，接续网络中交路集合还可以表示为W={} 1,2,…,i,…,j,…,2NE+NR，i和j为交路编号，设定分别表示交路i的开始时间和结束时间，对于任意交路i有一个运行里程Si.

3 数学优化模型构建

3.1 模型基本假设

(1)不考虑动车所的检修能力，理论优化方案超出检修能力时，通过人工干预进行调整.

(2)一般动车组的里程周期比时间周期要先到期，故暂不考虑检修时间周期限制.

(3)以动车组列车为最小单元，不考虑其重联与分解，同型号动车组列车的相同检修包的检修时间相同.

(4)动车组车型、初始运用状态、历史检修数据、检修包和交路信息等数据已知.

3.2 优化目标分析

为了提高动车组运用效率，在交路接续网络构建的基础上，以所有动车组担当交路的接续时间总和最小化作为主要优化目标，如式(1)所示.

式中tij为交路i和j之间的接续时间为动车组k担当完交路i后是否担当交路j的决策变量，若是=1，否则=0.

为了减少检修次数，降低检修成本，以动车组检修前相对于对应检修包里程周期的累计运行里程最大化为另一个优化目标.在不超期检修前提下，这可以转化为动车组检修前相对于对应检修包里程周期损失的可用里程（即检修包的里程周期减去检修前的累计运行里程）最小化，如式(2)所示.

式中P为检修包集合；m为检修包索引；Lm为检修包m的里程周期为动车组k在担当交路i和j之间是否安排检修包m作业的决策变量，若是为动车组k担当完交路i后，相对于检修包m最近一次检修的累计运行里程；λ为检修里程允许超期比例.

为了便于模型求解，设置时间与里程的换算系数ω，将双目标优化转化为单目标优化，最终的目标函数如式(3)所示.

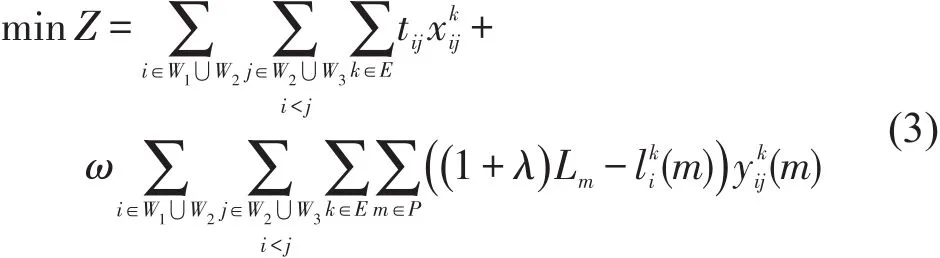
3.3 约束条件分析

任意一条计划开行交路和虚拟结束交路，有且只有一条由唯一动车组担当的前续交路，即

同理，任意一条虚拟初始交路和计划开行交路，有且只有一条由唯一动车组担当的后续交路，即

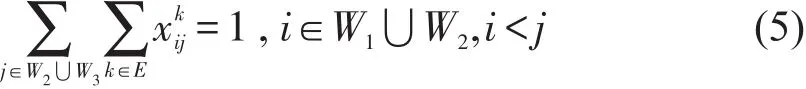
任意一条计划开行交路，其前续交路和后续交路由同一列动车组担当，即

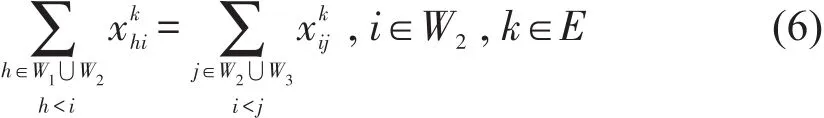
动车组车型与交路适用车型必须匹配，即

同理，动车组车型与检修包适用车型必须匹配，且只有当动车组k接续担当交路i和j时，才可以在二者间安排检修作业，即有

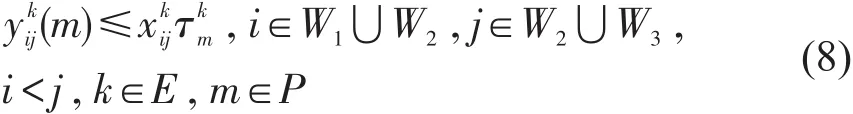
动车组必须满足接续时间标准T0，若动车组k在交路i和j间进行m包检修，还必须满足m包检修时间Tm的限制，即2

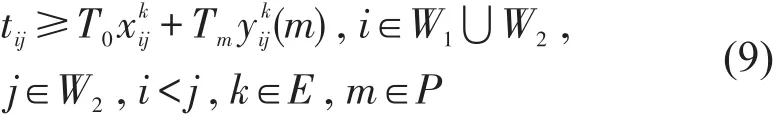
累计运行里程lkj(m)必须满足对应检修包的检修里程周期Lm的限制，避免超期检修，即

在计算接续时间tij时，当交路j是计划开行交路且可以接续交路i时，，否则tij=0；当交路j是虚拟结束交路，令tij=0，以避免将某些动车组因为处于库停状态而产生的时间计算在接续时间里.tij计算公式为

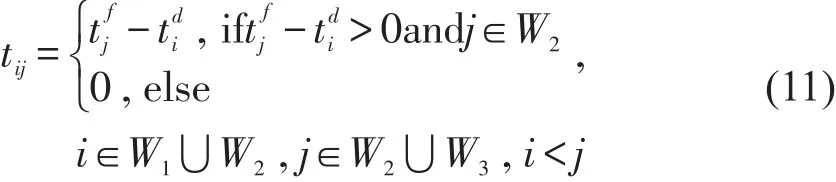
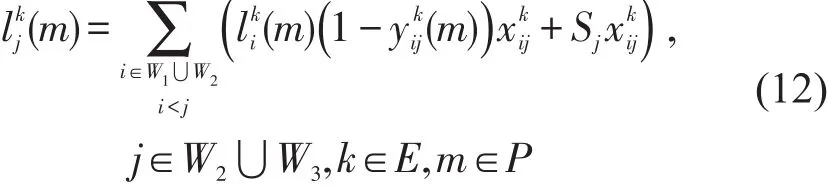
决策变量都满足0-1整数约束，即

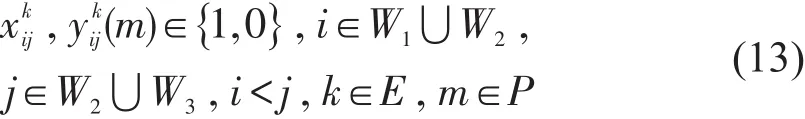
综合考虑式（3）～式（13），将优化目标函数和约束条件进行整合，可以得到动车组运用计划编制的数学优化模型为

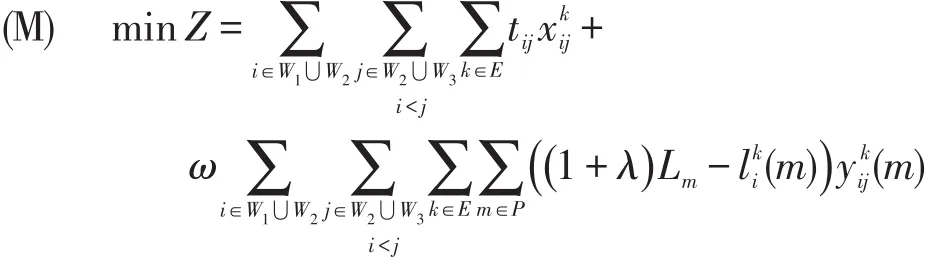
s.t.式（4）～式（13）

4 模型求解策略

本文基于具有操作简单、收敛速度快等特点的粒子群算法，根据模型的具体特点设计模型的优化求解策略.

4.1 模型的近似处理

为了便于模型求解策略的设计，首先对模型进行部分近似处理.基于模型构建之初交路排序的预处理，设置一个动车组担当交路的决策变量，r为交路索引，用于替代模型中决策变量，若动车组k担当交路r，则=1，否则=0.同理，设置一个动车组检修安排的决策变量(m)，用于替代模型中决策变量，若动车组k在担当完交路r后安排m包检修，则在求解中，首先确定)的取值，再据此确定的取值，最终得到动车组运用计划的优化方案.对于模型中涉及到的相应决策变量的问题，在求解策略设计和程序编写中进行具体处理.

模型中式(4)和式(5)共同说明任意交路都必须要有动车组去担当.在求解策略设计中，将该约束条件进行软化处理，并设置一个惩罚值M0，当出现一条交路无动车组担当时就在适应函数值中增加一个M0，假设有N0条交路无动车组担当，则总惩罚值为M0N0.

4.2 粒子群算法的具体应用

粒子数量为NQ，任意粒子q都有一个J维的位置矢量Xq=(xq1,xq2,…,xqJ)，在本文中每一个维度上粒子位置的取值代表动车组k是否担当交路r的决策变量的值，即为0-1整数.根据模型的目标函数值和惩罚值，计算粒子的适应函数值Fq(x)，并据此进行解的迭代更新.每个粒子具有一个飞行速度矢量Vq=(vq1,vq2,…,vqJ)和个体历史最优解Pq=(pq1,pq2,…,pqJ)，整个粒子群具有一个全局历史最优解Pg=(pg1,pg2,…,pgJ).根据xkr的定义确定粒子维度大小J=NE×(2NE+NR)，在第j个维度上j=k×r.粒子速度更新公式为

式中t为迭代次数；r1和r2是[0，1]之间的随机数；c1和c2是学习因子；粒子速度满足区间[-vmax,vmax]；ω(qt)是惯性权重，根据式(15)进行更新.

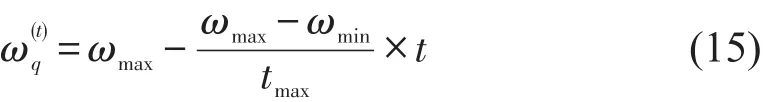
式中ωmax和ωmin分别表示最大和最小惯性权重；tmax表示最大迭代次数.

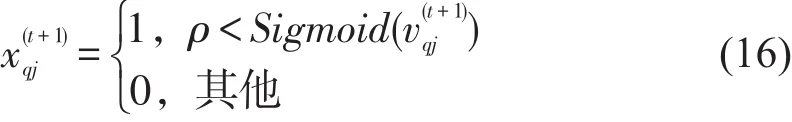
式中ρ为[0，1]之间的随机数，每次迭代中随机产生.Sigmoid函数是一种模糊函数，其公式为

通过对粒子在各维度上的位置所代表的动车组担当交路的解进行迭代更新，最终得到动车组运用方案的近似最优解.

4.3 模型求解的主要步骤

基于粒子群算法的主要求解步骤如下：

Step 1根据基础数据确定计划开行交路集合，并按开始时间进行先后排序.转Step2.

Step 2设置超期比例λ、换算系数ω、惩罚值Q0、粒子个数NQ、迭代次数tmax、粒子速度区间[Vmin,Vmax]、惯性权重区间[ωmin,ωmax]、随机数r1和r2、学习因子c1和c2等参数取值.将决策变量和取值均置零；随机生成粒子初始速度.设定迭代次数t=0时表示生成初始解.转Step3.

Step 3对于第t次迭代中的粒子q，根据动车组初始运用状态，确定当r≤NE时的取值，同时更新m).转Step4.

Step 4对于计划开行交路或虚拟结束交路r，为其随机分配动车组k，从动车组车型与交路是否匹配、接续时间是否满足、检修里程周期限制是否满足三方面判断动车组是否可以担当该交路.在该过程中，若动车组k对于交路r，不满足检修包m的检修里程周期限制，则令，并更新为动车组k最近一次担当的交路.若动车组k不可以担当交路r，则令，继续随机分配下一列动车组.若动车组k可以担当交路r，转Step5；若所有动车组均不担当交路r，则令r=r+1，直到交路遍历完毕，转Step7.

Step 5对于任意迭代次数t，判断t是否等于0.若t=0，则令，同时更新和最近一次担当的交路r′；若交路遍历完毕，则转Step7，否则令r=r+1，转Step4.若t≠0，则转Step6.

Step 8根据Fq(x)更新粒子的个体历史最优值Pq和粒子群的全局历史最优值Pg.转Step9.

Step 9若已达到最大迭代次数tmax，则计算结束，输出方案；否则令t=t+1，转Step3，进行下一次迭代.

5 算例分析

基于我国某动车运用所的部分实际数据进行动车组运用周计划编制的案例分析，并且周五、周六、周日三天在平日交路开行的基础上增加高峰交路.

选择CRH380CL型和CRH380AL型的动车组各5列.考虑到交路的结束时间一般都在当天24:00以前，同时为了简化算例计算，设定所有动车组的可用时间均为00:00.动车组信息如表1所示.

表1 动车组信息Table 1Motor trainset information

为CRH380CL型和CRH380AL型动车组分别选择3条可担当的平日交路、1条高峰交路.交路信息如表2所示.

表2 交路信息Table 2Route information

每种型号的动车组都有多个不同的检修包，例如一级修、I2修、M1修、牵引机注油、轮对镟修、空心轴探伤等，每个检修包的检修里程周期及检修时间不尽相同.本文只选择一级修、I2修、M1修三个检修项目进行计算试验，其信息如表3所示.

表3 检修包信息Table 3Maintenance project information

根据动车所统计的动车组当前总运行里程和每个检修包最近一次检修时的总运行里程，可以计算出动车组相对于每个检修包最近一次检修后的累计运行里程，具体如表4所示.

表4 动车组累计运行里程（km）Table 4Accumulated mileage of motor trainset(km)

其他相关参数设置如下：设定λ=10%，ω=1.1，Q0=100 000，NQ=30，r1=r2=0.5，c1=c2=2.0，tmax=2 000，速度区间为[-4,4]，惯性权重区间为[0.4,0.9].借助visual studio 2010编程平台，采用C++语言，实现算法程序设计.

由于启发式算法计算结果具有一定的波动性，本文进行10次优化求解，从中选择最优解作为最终优化方案.在4G内存、i5处理器、Win8操作系统的PC机环境下，经过112秒计算，得到动车组运用计划的近似最优方案，如图2所示.

图2 动车组运用计划优化方案Fig.2 Optimization scheme of motor trainset utilization scheduling

对于图2所示的动车组运用计划优化方案，动车组的总接续时间为61 230 min，检修时总损失的可运用里程为27246 km.交路都有对应的动车组担当，保证了计划周期内运输任务的正常完成，并且动车组在检修前其累计运行里程都尽可能地贴近了检修里程周期上限.由于动车组的一级修检修里程周期较短，计划中一级修安排较多，只有动车组e3和e5进行了I2修.一般而言，动车组的一级修安排在夜间进行，在该优化方案中，对于一级修完成后没有立即去担当交路的动车组，可根据动车所检修能力适当调整动车组的一级修时间.

6 研究结论

本文基于交路接续的思想，构建了动车组的接续网络，建立了优化模型，并设计了求解算法.通过算例分析，说明运用本文提出的模型和算法可以生成动车组运用计划的初始方案，为实际生产中动车所编制动车组运用计划提供参考依据.然而，在实际中动车组运用计划的编制不仅受检修里程周期的约束，还受检修时间周期的限制，尤其是对于备用时间较长的动车组.此外，为了更好地提高动车组运用效率，不同型号动车组之间的相互替代等情况也应该考虑.在未来的研究中将对这些问题做进一步探讨.

[1]Erwin Abbink,Bianca van den Berg,Leo Kroon,et al. Allocationofrailwayrollingstockforpassenger trains[J].Transportation Science,2004,38(1):33-41.

[2]Luis Cadarso,Ángel Marín.Improving robustness of rolling stock circulations in rapid transit networks[J]. Computers&Operations Research,2014,51:146-159.

[3]Giovanni Luca Giacco,Donato Carillo.Short-term rail rolling stock rostering and maintenance scheduling[J]. Transportation Research Procedia,2014,3:51-659.

[4]陈玲娟.遗传算法在动车组运用计划编制中的应用[J].交通运输工程与信息学报，2009，7(2)：67-71. [CHEN L J,Application of genetic algorithms to electric multiple unit scheduling[J].Journal of Transportation Engineering and Information,2009,7(2):67-71.]

[5]佟璐，聂磊，赵鹏.蚁群算法在动车组运用问题中的应用[J].交通运输系统工程与信息，2009，9(4)：161-167.[TONG L,NIE L,ZHAO P.Application of ant colony algorithm in train-set scheduling problem[J]. Journal of Transportation Systems Engineering and Information Technology,2009,9(4):161-167.]

[6]苗建瑞，王莹，杨肇夏.基于最优接续网络的动车组交路计划优化模型与算法研究[J].铁道学报，2010，32 (2)：1-7.[MIAO J R,WANG Y,YANG Z X.Research on the optimization of EMU circulation based on optimized connecting network[J].Journal of the China Railway Society,2010,32(2):1-7.]

[7]李华.高速铁路动车组运用计划编制理论与方法研究[D].北京交通大学，2013.[LI H.Theory and method studies on EMU scheduling problem for high speed railway[D].Beijing Jiaotong University,2013.]

[8]王忠凯，史天运，张惟皎，等.动车组运用计划和检修计划一体化编制模型及算法[J].中国铁道科学，2012，33(3)：102-108.[WANG Z K,SHI T Y,ZHANG W J, et al.Model and algorithm for the integrative scheduling of EMU utilization plan and maintenance plan[J].China Railway Science,2012,33(3):102-108.]

Optimization Model and Algorithm for Motor Trainset Utilization Scheduling Based on Routes Connection

LI Jian1,LIN Bo-liang1,GENG Ling-qian2,CHEN Lei1,WANG Jia-xi1,WU Jian-ping1

(1.School of Traffic and Transportation,Beijing Jiaotong University,Beijing 100044,China;2.Transportation Division, Shenyang Railway Bureau,Shenyang 110001,China)

A 0-1 integer programming model is constructed for the motor trainset utilization scheduling by using switching network method,on the basis of initial utilization state and historical maintenance data.The model minimizes the total connection time and maximizes the accumulated mileage before maintenance of all motor trainset.The model takes the matching degree between the trainset and the route into consideration, as well as the additional routes at passenger flow peak.It also takes the maintenance mileage standard of motor trainset and connection time standard of route as the key constraint condition.In terms of the solution method for the model,a fast solving method is put forward based on particle swarm optimization.A case study verifies the effectiveness of the optimization model and solving method,and provides a reference for the motor trainset utilization scheduling.

railway transportation;motor trainset utilization scheduling;routes connection;0-1 integer programming model;particle swarm optimization

1009-6744（2015）05-0172-06

U279.2

A

2015-04-07

2015-07-01录用日期：2015-07-06

中央高校基本科研业务费专项资金资助（2014YJS069）；国家自然科学基金资助(51178031)；中国铁路总公司科技研究开发计划课题（2014J006-C）.

李建（1989-），男，四川宜宾人，博士生. ＊

bllin@bjtu.edu.cn