基于ADAMS对麦弗逊悬架、双横臂悬架动力学性能对比研究

孙 艳

(辽宁工业大学 汽车与交通工程学院)

1 前悬架动力学仿真模型的建立

1.1 动力学软件ADAMS 介绍

MSC.ADAMS 是一款在机械设计制造领域应用最普遍，涉及领域最多的一款虚拟样机软件。ADAMS 下面涉及很多专业领用，其中ADAMS/Car 是其中一款专门应用于轿车研究开发的软件包，大量吸收了奥迪、宝马、沃尔沃等国际大型汽车公司的专业经验，应用ADAMS/Car 对整车以及各个悬架子系统设计研究，可极大减少汽车生产领域对设计人员工作经验的依赖。

1.2 前悬架仿真模型的建立

应用ADAMS/Car 建立动力学仿真模型，是一个自上而下的建模过程。首先在Template 模块，建立汽车系统的模版文件，并为建立好的模版文件匹配属性文件和通讯器;然后，在Standard 界面将模版文件转化为子系统文件，子系统文件跟模版文件的主要区别在于，子系统文件中各个系统有前、后之分，而模版文件只是各个部件的模版，不带有前、后等定义，必须经转换为子系统文件，才能实现定义。

本文直接采用ADAMS 共享数据库中的麦弗逊式独立悬架跟双横臂独立悬架的模版文件作为建立悬架子系统的模版，所以不需在ADAMS/Car Template 再次建立。本文在ADAMS Standard 界面将共享数据库中的麦弗逊悬架跟双横臂悬架的两个悬架模版文件定义为子系统文件，完成两悬架子系统文件的建立。再将两前悬架子系统文件跟ADAMS悬架仿真试验台进行组装，分别建立两个本文用于仿真的前悬架仿真模型。

2 仿真试验与数据处理

2.1 仿真试验

ADAMS/Car 中提供了三种试验方法对悬架进行性能分析，这三种方法分别是:双轮同向跳动试验、双轮反向跳动试验、单轮跳动试验。其中，双轮同向跳动试验方法是应用最普遍的一种试验方法，本文对两悬架性能分析对比就采用该试验方法。

2.2 数据处理

(1)对前轮定位参数的影响

汽车前轮定位参数主要包括外倾角、后倾角、主销内倾角、前束角。

外倾角随车轮跳动的变化量包括两部分，一是由车身侧倾产生的车轮外倾变化，二是由车轮相对车身的跳动而引起的外倾变化。在车辆行驶过程中，外倾角的变化对直线行驶的稳定性以及稳态相应等特性都有很大影响，取值范围一般在－2.0°～0.5°(50 mm)。如图1 所示，在车轮上下跳动50 mm 的过程中，麦弗逊式独立悬架的变化范围为－0.75°～1.28°，双横臂式独立悬架的变化范围为－1.21°～0.74°，双横臂式独立悬架的外倾角在随车轮跳动变化过程中，由于麦弗逊式独立悬架。

图1 两悬架外倾角随车轮跳动变化曲线

主销后倾角是在汽车行驶过程中偶遇外力稍有偏转时，产生与车轮偏转方向相反的力矩，保证汽车稳定直线行驶。轿车的主销后倾角的取值范围一般为3°～10°(50 mm)。如图2 所示，麦弗逊式独立悬架的主销后倾角随车轮跳动的变化量为4.70°～5.47°，双横臂式独立悬架随车轮跳动的变化量为5.37°～5.49°，两悬架的主销后倾角的变化量均满足取值变化范围要求，但双横臂式独立悬架的注销后倾角随车轮跳动的变化量明显小于麦弗逊式独立悬架系统，所以仍是双横臂式独立悬架系统更优。

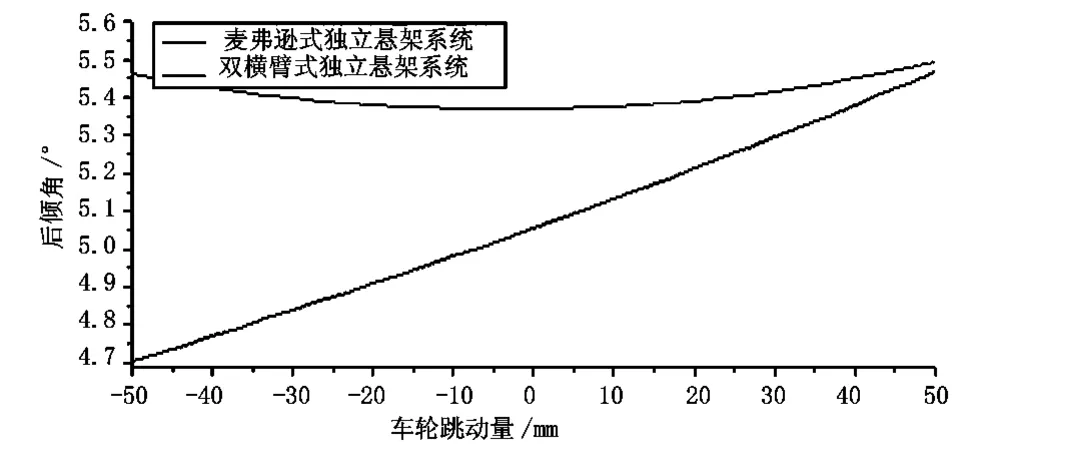
图2 两悬架后倾角随车轮跳动变化曲线

主销后倾角之所以能够实现产生与车轮行驶相反的力矩，是通过主销后倾拖距实现的。该力矩产生一个与轮胎侧偏角相似的附加转向角，能够使汽车在行驶过程中趋于增加不足转向，有利于改善汽车的稳态转向特性。设计要求主销后倾拖距随车轮在上跳形成中增加，如图3 可以看出，双横臂的主销后倾角拖距随车轮上跳而上升，符合设计要求。

图3 两悬架后倾拖距随车轮跳动变化曲线

主销内倾角的主要作用是在汽车低速行驶时对汽车的主动回正作用。设计过程中，主销内倾角通常去较大值，规定为7°～15°。如图4 所示，麦弗逊式独立悬架的主销内倾角随车轮跳动过程的变化范围为11.50°～13.31°，双横臂式独立悬架的变化范围为9.06°～11.35°，均满足设计要求。

图4 两悬架内倾角随车轮跳动变化曲线

前束角在设计过程中一般取成0 或弱负值，且随车轮上跳过程而下降，这样有利于汽车行驶过程中获得不足转向。如图5 所示，麦弗逊式独立悬架随车轮上下跳动50 mm的过程中的变化范围为－1.06°～1.01°，双横臂式独立悬架的变化范围为－1.31°～2.23°，两者的变化范围均较大，但双横臂式独立悬架的前束角随车轮上升过程而下降，变化趋势正确，比麦弗逊式独立悬架的变化合理。

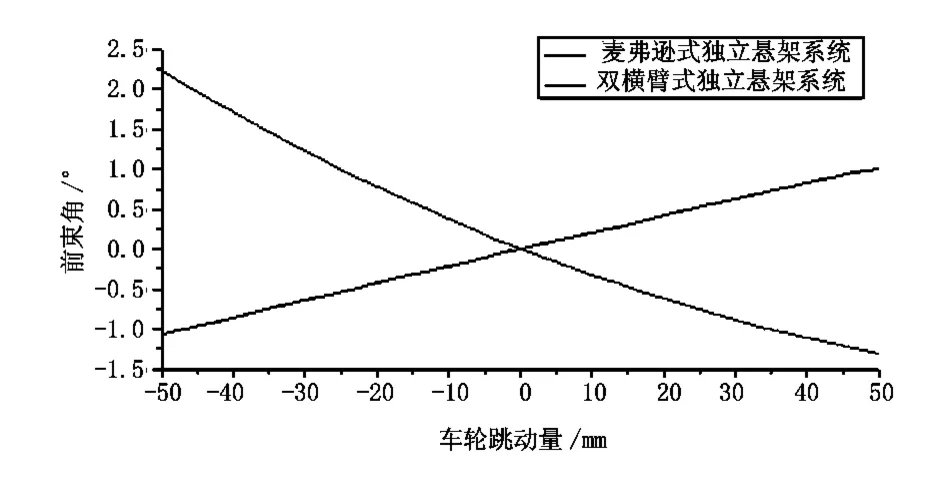
图5 两悬架前束角随车轮跳动变化曲线

(2)对侧倾特性的影响

汽车设计过程中，轿车的侧倾外倾系数变化范围为0.61～0.88° /(°)时，可满足汽车的不足转向要求。如图6所示，麦弗逊式独立悬架的侧倾外倾系数在随车轮上下跳动50 mm 的过程中的变化范围为0.77°～0.91°，双横臂式独立悬架的变化范围为0.65°～0.83°，双横臂式独立悬架的侧倾外倾系数的变化范围满足汽车设计过程中的不足转向要求，麦弗逊式独立悬架的设计范围超出了不足转向要求，双横臂式独立悬架具有较优的侧倾外倾系数。

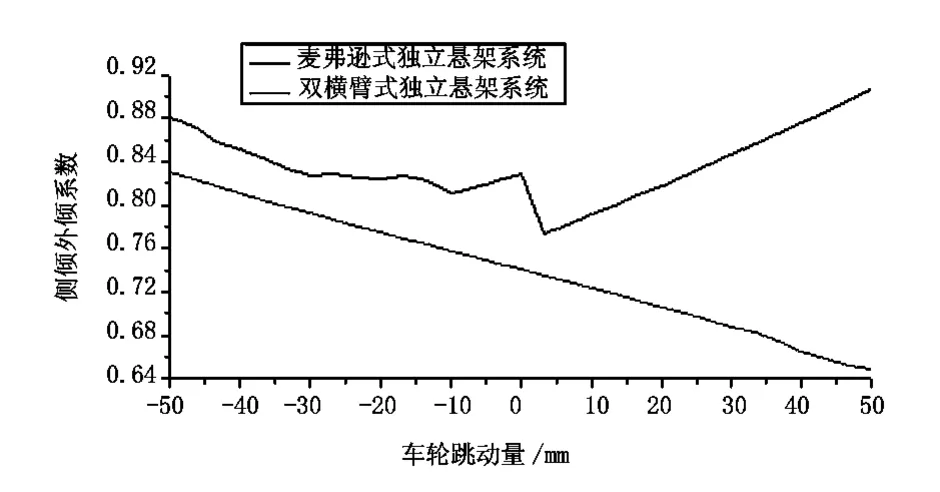
图6 两悬架侧倾外倾系数随车轮跳动变化曲线

汽车设计过程中，增加前悬架的侧倾角刚度有利于汽车获得良好的不足转向，且在汽车转弯时，较大的侧倾角刚度，可较好地抑制车身侧倾角的增大。

由图7 知，在平衡位置处，麦弗逊式独立悬架的侧倾角刚度为43.39N.m/°，双横臂式独立悬架的侧倾角刚度为154.28N.m/°。双横臂式独立悬架的侧倾角刚度要大于麦弗逊式独立悬架的侧倾角刚度，因此双横臂式独立悬架具有较好的侧倾角刚度值。

图7 两悬架侧倾角刚度随车轮跳动变化曲线

(3)对纵倾特性的影响

制动点头量和加速抬头量反应了汽车在制动和加速时悬架对轮心垂直位移的约束能力。

麦弗逊式独立悬架的制动点头量的变化范围为8.82～9.93 mm/g，不及双横臂式独立悬架制动点头量的变化范围4.39～5.38 mm/g。

加速抬头量跟制动点头量随车轮跳动的变化曲线可知，安装横向稳定杆对整车的纵倾特性也有一定程度的改善。同样，麦弗逊式独立悬架的加速抬头量的变化范围1.73～5.11 mm/g，也比不上双横臂式独立悬架的变化范围－9.16°～－3.75° mm/g。综合，图8 可以得出双横臂式独立悬架具有较好的纵倾特性。

图8 两悬架制动点头量随车轮跳动变化曲线

［1］陈家瑞.汽车构造(下册)［M］.北京:机械工业出版社，2005.

［2］陈军.MSC.ADAMS 技术与工程分析实例［M］.北京:中国水利水电出版社，2008.

［3］丁亚康，翟润国，井绪文.基于ADAMS/INSIGHT 的汽车悬架定位参数优化设计［J］.汽车技术，2011，(5):33－36.

［4］王卡.麦弗逊式悬架结构的有限元分析［D］.西南交通大学，2008.6.