采用圆投影和序贯相似检测的图像匹配技术

贾晓芬，赵佰亭，周孟然，杨芝权

(安徽理工大学电气与信息工程学院，安徽淮南232001)

模板匹配是基于已知的模板在搜索图中确定最佳匹配位置的过程，是数字图像处理中的一个重要课题，已广泛应用于飞行制导领域，目标检测等.近年来模板匹配研究获得了一些有效的算法[1－2].模版和搜索图在实际使用中往往具有比较大的旋转角度，现有的基于最小均方差的方法、基于区域灰度相关的归一化积相关和其他结构的模板匹配算法，其基本匹配原理是连续比较模版和搜索图之间对应灰度值的相关性，仅仅在旋转角度较小的情况下才有效.近年来国内外学者相继提出了一些可以任意旋转匹配的方法，文献[3]提出了方向码法，利用方向码的直方图进行比较分析，但是该方法具有计算量大速度很慢的缺点，对于一个未知的任意角度需要进行360°的旋转才能和搜索图匹配.文献[4]中提出了SIFT算法，该算法利用128维特征向量解决旋转不变的匹配，计算量较大，且匹配速度慢.文献[5－6]基于圆投影向量的旋转不变性，用圆的各向同性和投影特征进行任意旋转角度的匹配，但匹配速度也不够理想.

随着对图像匹配技术的研究，各种复杂的、高精度的算法被相继提出.Kim在文献[7]设计了一种旋转判别模板匹配算法，算法中对径向投影进行离散傅立叶变换，利用变换的系数来计算旋转变量.符艳军[8]等利用小波变换压缩图像减少搜索空间，利用矩特征减少待匹配位置相似性测量的计算量，获得了较好的匹配速度.文献[9]结合惯性导航的特点，提出了一种高精度、高速度的匹配算法.郭莉莎[10]等基于多尺度，应用 FAST－9检测子提取特征点，实现了快速匹配算法.吴振国[11]等提出了一种具有仿射不变性的匹配算法，该算法中特征点的提取利用Harris－Laplace算法实现.

本文针对现有的高精度匹配方法复杂度较大，圆投影算法的匹配慢的缺点，设计了一种新的基于序贯相似检测原理的匹配算法，仿真结果表明该算法计算速度有了明显提高，实现了计算复杂度和匹配速度的折衷.

1 圆投影及圆投影向量

1.1 圆投影

在圆投影的匹配算法中，旋转不变量是通过圆的投影特性来描述的，这样就可以实现模板与搜索图的在进行角度的旋转时的图像快速匹配问题[5].如图1 所示，f(x，y)表示坐标(x，y)处的像素值，以图像的中心为坐标原点o(α，β)，采用极坐标来表示，由 x=rcosθ和 y=rsinθ可得 f(rcosθ，rcosθ).当半径为r时的，定义此时的投影值p(r)为:

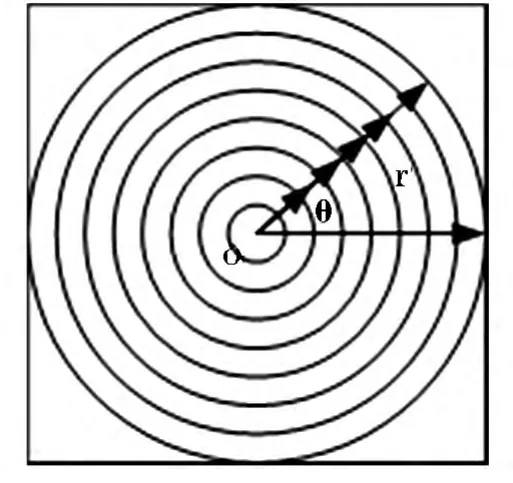
图1 圆投影示意图

p(r)的离散形式可以写成:

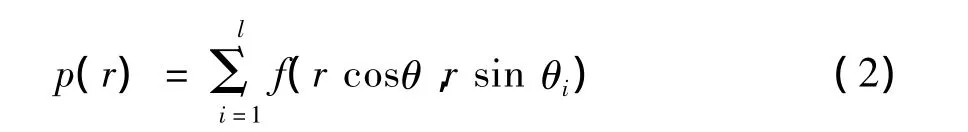
其中:r=1，2，3，4，…，R;l是圆周的等分数目;R 为图像最大的内切圆半径.

图像投影的结构是个圆，所以当图像旋转时投影在圆上的像素会随着图像的旋转而同心、同半径的进行旋转，在旋转中p(r)是固定量不发生改变.那么当半径r不同时，所对应的图像的圆投影向量如下:

1.2 圆投影向量的重构

由于p(r)对噪声、光照和对比度变化的敏感性，使之的在实际应用中受到了很大的限制，不适合推广使用.针对这个问题，文献[6]中对传统的圆投影向量进行了重构，得到了新的圆投影向量:

重构的圆投影向量p'(r)，具有灰度平移不变性，因而，新图像的圆投影向量就可以表示成:

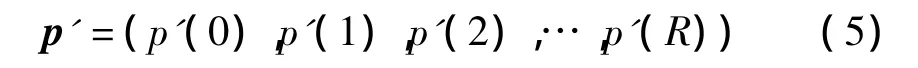
2 基于亚模板的圆投影向量之间距离的跳跃匹配

本文用到的定义和符号含义规定如下，T表示模板，其大小为M×M;S是一个长宽为Nx×Ny的搜索图;在搜索图(u，v)处对应的模板窗口大小为S(u，v).其中 1≤u≤Nx－ m+1，1≤v≤Ny－ m+1.

2.1 圆投影向量的匹配

进一步的将二维图像T和S(u，v)投影到一维空间中，可以得到新的圆投影向量PT和PS(u，v)，它们是不跟随旋转而变化的，PT和PS(u，v)如式(6)和式(7)所示:

其中:R是模板中最大的内切圆半径.

在匹配时，归一化积相关是一种常用的相似度量:

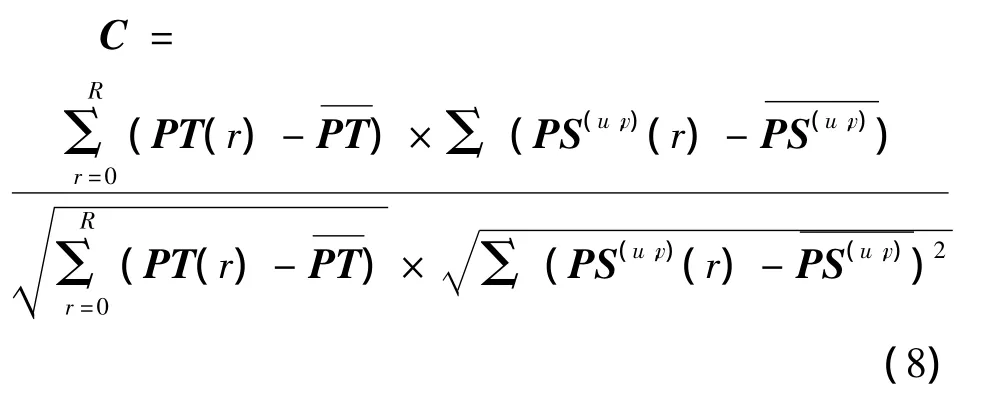
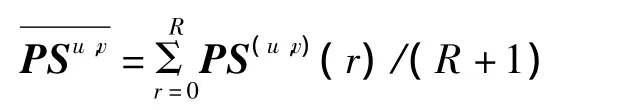
文献[6]就是使用(8)式为相似度量函数，公式(8)中参数多、变量复杂，计算量很大，运算速度慢.

序贯相似检测方法对文献[6]中的方法做了进一步的改善，该方法不在不断地计算圆投影向量的差值和标准差，相应的计算量大幅降低.该方法首先随机抽取r个不相同的样本，则其差L1的范数值定义为D(r):

其中:0＜r≤R.

从式(9)中可以看出D(r)是单调递增的，当D(r)满足式(10)时就可以停止比较:

该方法相对于文献[6]使用公式(8)的方法有所改进，当r比较小时会减少一定的计算量工作，但是由于要求遍历所有的位置，在应用时仍然不能满足实际需求，本文针对这个问题，设计了基于自适应跳跃的圆投影向量的匹配算法.

2.2 基于自适应跳跃的圆投影向量的匹配

T的亚模板用 Tsub表示.Tsub和 S(u，v)sub即是 T和S(u，v)的一部分，如图2、3所示.图中边缘大小用 m表示，则亚模板和亚窗口可以表示为(M－m)×(M－m)，一共m2个窗口，其中m的参考取值范围为 3 ～7[12－13].

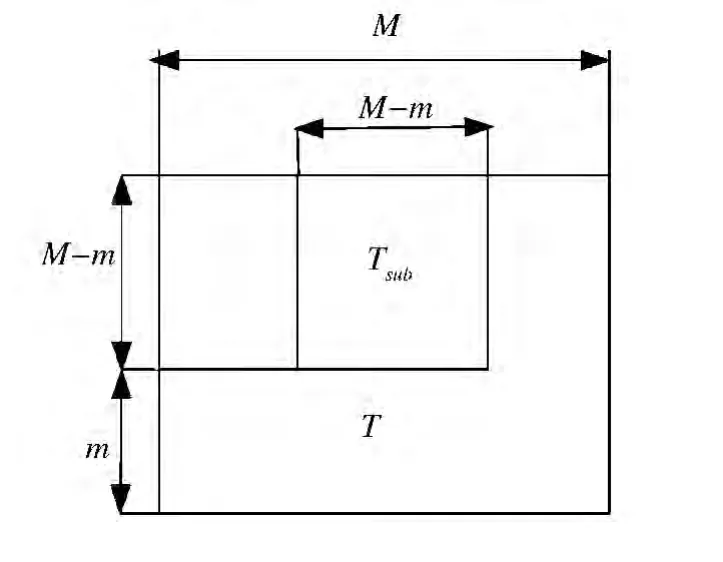
图2 T的亚模板示意图

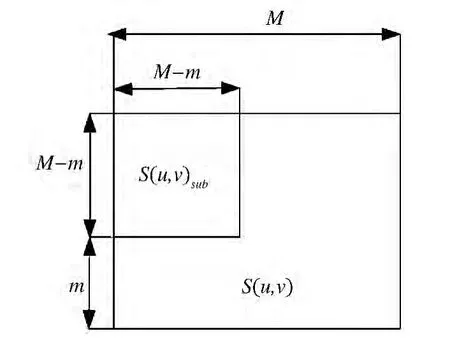
图3 S(u，v)的亚窗口示意图

其中:Rsub是Tsub和)的最大内圆半径.

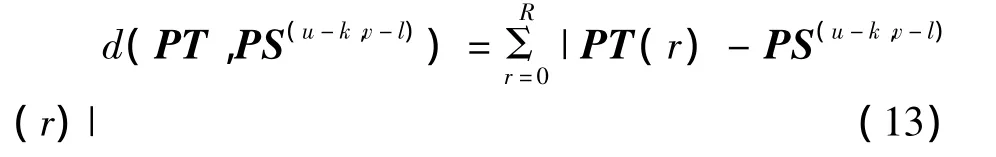
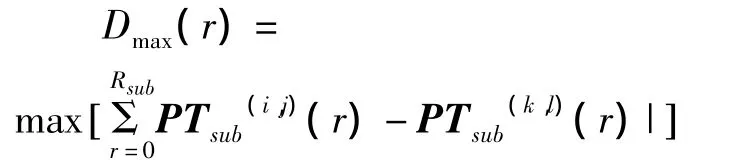
其中:

2.3 算法设计

本文设计的匹配算法的具体步骤如下:

Input:T(1，1)sub是参考亚模版;PT(1，1)sub是相应的圆投 影 向 量;S(u，v)sub为亚窗口;滑动范围 From

1)根据式(10)计算D(r);

2)计算 S(u－k，v－1)和 T 的圆投影向量之差;

3)对[2]计算结果取L1范数;

6)Else 按照滑动范围 From SNx－M+1，Ny－M+1to S1，1，跳过相邻匹配点继续匹配下一匹配点;

7)If D(r)＜thresh+D max(r)，存储匹配次数t;

8)取MAX(t)投入下一步的带匹配点中;

9)利用公式(4)重构圆投影向量 P'T'和P'S(u，v);

10)利用公式(8)计算相似度量，具有MAX(C)的点为最佳匹配点.

3 实验结果及分析

3.1 实验结果

仿真实验所用计算机配置为奔腾双核E5400的CPU，主频为 3 GHz，内容为 2 GB，在 MatlabR2009b的编译环境中进行.为了验证所提算法的有效性和可行性，针对图4所示的6幅经典图像进行了仿真实验，并与文献[6]、式(9)和文献[8]所提的方法进行对比分析，具体实验步骤如下:

第1步:以30°为间隔逆时针旋转原始图像;

第2步:从旋转后的图像中分别截取63×63的模板;

第3步:原始图像中加入高斯白噪声(方差0.01);

第4步:分别进行图像匹配分析.

图4为测试搜索图(图1～6按从左至右、从上至下排列)，图5为测试搜索图1的原始图像，图6为从左至右分别旋转 30°、60°、90°的模板图，图 7为搜索图1的匹配示意图.以仿真时间作为算法的性能指标进行对比分析，仿真时间如表1所示.对比本文提出的算法和方法1、2、3可见本文提出的算法时间最短效果最好.

本文仅以搜索图1为例介绍完整的一个匹配过程，搜索图1的原始图和仿真结果分别如图5～7所示.

表1 不同搜索图的匹配时间

图4 测试搜索图(图1～6按从左至右、从上至下排列)

图5 搜索图1

图6 从左至右分别旋转30°、60°、90°的模板图

图7 搜索图1的匹配示意图

对于简单背景的搜索图来说，本算法的匹配精度高达约90%，正确率较高，如图8(A)所示在搜索图4中仿真100次得到模板中心的匹配点坐标;而当背景较为复杂的搜索图中存在虚假的目标时，能够成功匹配的精度为75%.在搜索图1中仿真100次得到模板中心的匹配点坐标如图8(B)所示.

3.2 结果分析

从表1中可以看出，本文提出的算法耗时远小于方法1和方法2.其中采用穷尽式搜索的方法1，需要计算每一个匹配点的圆投影向量，耗时最长;方法2由于采用了序贯相似检测，在穷尽式搜索的过程中可以不用匹配不必要的半径上的像素值，所以算法运算时间优于方法1;而方法3是通过牺牲待匹配位置的相似性度量来提高匹配算法的快速性;本文设计的图像匹配算法，在搜索过程中跳跃式的前进，可以跃过大量的搜索匹配点，这样具有更好的快速性.虽然在搜索背景较为复杂的图像上进行匹配时的匹配精度较低，但是仿真结果显示，这并不是由于本搜索算法所造成的.从图9(A)可以看出，图像中有3簇具有最大的r值的区域，分别对应了一个真目标和两个伪目标，而图9(B)中具有最大r值的区域只有一个，对应着真目标的所在.虽然本算法跃过了大量的搜索匹配点，但是并未丢失正确的匹配点.

图8 模板的中心点坐标图

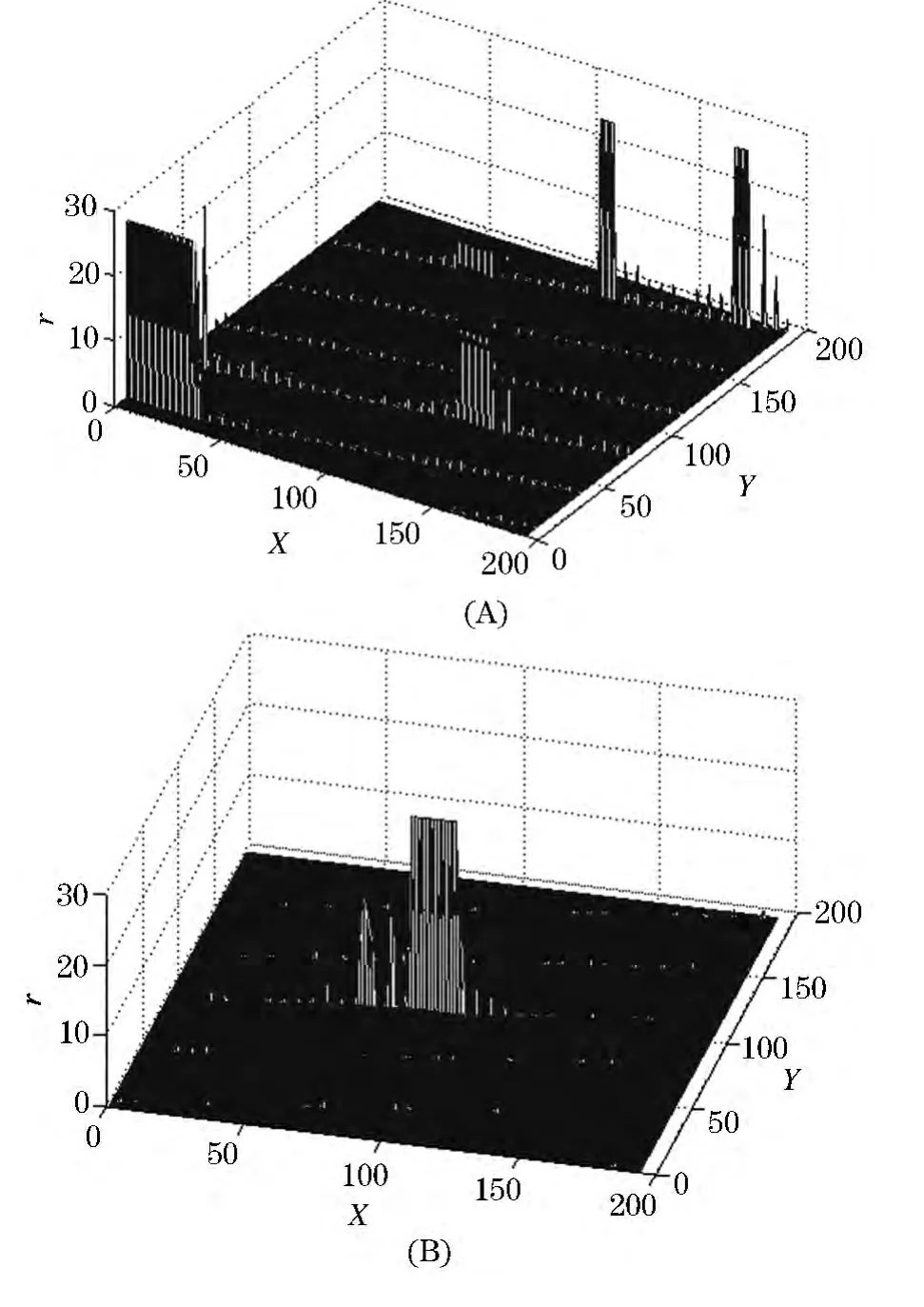
图9 搜索图的搜索路径

4 结语

本文采用圆投影向量匹配，解决了匹配模板与搜索图间具有较大旋转角度时的匹配问题，算法中采用跳跃式搜索方法，在约简掉冗余的匹配点的匹配问题的情况下，能够保证正确匹配信息的不丢失，不会降低匹配精度.前期的搜索过程的匹配点的约简，可以减少匹配计算量，降低算法时间，后期的精确匹配又不会影响算法精度.仿真结果证明了本算法的合理性和有效性.

[1]ZITOV B，FLUSSER J.Image Registration Methods:A Survey[J].Image and Vision Computing，2003，21(11):997 －1000.

[2]BROWN L G.A Survey of Image Registration Techniques[J].ACM.Computing Survey，1992，24(4):325－376.

[3]ULLAH F，KANEKO S.Using orientation codes for rotation －invariant template matching[J].Pattern Recognition，2004，37(2):201－209.

[4]LOWE D G.Distinctive image features from scale－invariant keypoints[J].International Journal of Computer Vision，2004，60(2):91－110.

[5]TSAI D M，CHIANG C H.Rotation－invariant pattern matching using wavelet decomposition [J].Pattern Recognition Letters，2002，23(1－3):191－201.

[6]徐亦斌，王敬东，李 鹏.基于圆投影向量的景象匹配方法研究[J].系统工程与电子技术，2005，27(10):1725－1728.

[7]KIM H Y.Rotation－discriminating template matching based on Fourier coefficients of radial projections with robustness to scaling and partial occlusion [J].Pattern Recognition，2010，43(3):859－872.

[8]符艳军，程咏梅，潘 泉，等.基于不变矩的景象匹配辅助导航快速匹配算法[J].系统工程与电子技术，2011，33(4):847－850.

[9]王先敏，曾庆化，熊 智，等.结合惯性导航特性的快速景象匹配算法[J].系统工程与电子技术，2011，33(9):2055－2059.

[10]郭莉莎，李俊山，朱英宏，等.基于多尺度FAST－9的图像快速匹配算法[J].计算机工程，2012，38(12):208－210.

[11]吴振国，杨红乔.一种具有仿射不变性的图像匹配算法[J].计算机工程，2013，39(8):215－218.

[12]KAWANISHI T，KUROZUMI T，KASHINO K，et al.A fast template matching algorithm with adaptive skipping using innersubtemplates’distances[C]//Proc.of the 17th International Conference on Pattern Recognition，2004，3:654－657.

[13]赵佰亭，贾晓芬.基于遗传算法寻优的支持向量机图像插值方法[J].哈尔滨商业大学学报:自然科学版，2013，29(2):212－217.